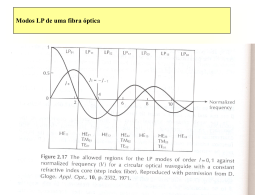
AUTOR:
ALMIR
WIRTH
LIMA
JUNIOR,
ESPECIALIZADO NA TELEKOM ALEMÃ, MESTRE
E DOUTOR PELA UNIVERSIDADE FEDERAL DO
CEARÁ (U.F.C)
Dispersões
S= Dispersão Intermodal
Conforme o próprio nome indica a dispersão intermodal, também conhecida
como dispersão modal, trata-se de um fenômeno que ocorre quando existem
diferentes modos se propagando dentro de uma fibra óptica. Portanto, este tipo
de dispersão ocorre apenas em fibras ópticas multimodo. Tendo em vista que
os modos dentro da fibra óptica possuem diferentes velocidades de grupo,
cada um deles percorre sua trajetória (do início ao fim da fibra óptica) em
períodos de tempo diferentes. Desta forma, quando um pulso óptico atravessa
uma fibra óptica multimodo, eles são alargados (surge dispersão), e se
misturam aos pulsos adjacentes. Este efeito limita tanto a banda passante da
fibra óptica multimodo, como o comprimento máximo do enlace óptico.
Consideremos o pulso luminoso que incide numa fibra. A sua potência será
distribuída entre os vários modos de propagação e, apesar de todos partirem
da extremidade inicial da fibra no mesmo instante, chegarão à extremidade
final da fibra em instantes diferentes devido aos diversos diferentes caminhos
percorridos, alargando o pulso de saída e, portanto, limitando a capacidade de
transmissão. Note que o modo de ordem mais baixa possui velocidade de
grupo com valor em torno de c/nnúcleo, uma vez que esse modo está
praticamente contido no núcleo. Por outro lado, o modo de ordem mais alta
possui velocidade de grupo em torno de c/nrevest., uma vez que uma parte do
campo é transportado na região do revestimento, a qual possui índice de
refração menor que a região do núcleo.
F= Figura 5.23 - Dispersão de pulso em fibra multimodo de índice degrau
Para fibras típicas de índice degrau, a dispersão modal (dm) é da ordem de
20ns/Km a 65ns/Km. Esta dispersão é muito alta e permite apenas algumas
dezenas de conversações telefônicas por alguns quilômetros de fibra.
Como a velocidade de propagação ao longo da fibra óptica varia de acordo
com o inverso do índice de refração, existe a possibilidade de se compensar ou
equalizar as diferenças de tempo entre os modos variando-se o índice de
refração em função do raio do núcleo.
Chegamos, então, à fibra com índice de refração gradual, que possui um valor
máximo de índice de refração no centro do núcleo, diminuindo radialmente em
direção à casca. Conseguimos, assim, uma velocidade de propagação menor
para os modos de percurso mais curto, e uma velocidade maior para os modos
que percorrem o maior trajeto.
Não há fibra óptica com índice de refração gradual capaz de equalizar a
velocidade de grupo de todos os modos em uma fibra multimodo de simetria
circular, porém se o perfil do índice de refração obedecer a lei exponencial
conforme a equação abaixo, então, se obterá uma redução maior nesta
diferença de tempo (atraso).
n (r ) = n1 (1 − 2 ⋅ Z ⋅ f (r ))
2
Onde:
n1 = índice de refração no eixo da fibra ótica.
2
2
n1 − n 2
Z=
2 ⋅ n1
n2= índice de refração da casca.
f(r) = função perfil
f(r) = 0, para r =0; f(r) =1, para r = a
r = distância do eixo da fibra ao ponto em questão.
Demonstra-se que o atraso modal máximo sofrido por uma radiação é:
A max =
Dn 2
c (ns/km);
D=
n1 − n2
n1
Onde:
n1 = Índice de refração do núcleo
n2 = Índice de refração da casca
F= Figura 5.24 - Dispersão Intermomodal
Numa fibra com D = 0,01 e n1 = 1,5, resulta um atraso de 500ns/km. Este
atraso corresponde a uma banda de modulação útil de apenas 0,5 a 1,0MHz.
Para aumentar a banda de transmissão da fibra, existem duas alternativas. A
primeira alternativa consiste em se projetar a fibra óptica com o diâmetro do
núcleo muito pequeno e um índice de degrau também pequeno, de tal forma
que a fibra ótica admite apenas um modo de propagação. Estas fibras,
denominadas fibras monomodo, apresentam maiores dificuldades de
fabricação, e devem ser tomadas precauções com relação ao acoplamento
com os emissores e receptores de pulsos ópticos, devido às pequenas
dimensões do núcleo (5 a 10µm).
S= Dispersão Intramodal
Não existe dispersão intramodal em fibras ópticas monomodo. Entretanto,
mesmo em fibras monomodo existe dispersão, a qual é denominada de
dispersão intramodal.
SS=Dispersão material
A dispersão material surge devido à dependência do comprimento de onda em
relação ao índice de refração. Mesmo tratando-se de pulso com largura muito
estrita, esse pulso é constituído por várias componentes, cada uma com
determinado comprimento de onda. O alargamento do pulso constituído por
uma faixa espectral ∆λ é obtido através da seguinte relação:
∆τ = L Dm ∆λ , onde L é o comprimento do enlace óptico, e Dm é denominada
de coeficiente de dispersão material. A dispersão é expressa em alargamento
por unidade de comprimento.
A equação seguir fornece o valor aproximado de Dm.
Dm ≈ −
λ δ 2n
c δλ2
A figura a seguir mostra o gráfico de Dm em função de λ.
Figura 5.24.1 Coeficiente de dispersão material versus comprimento de onda
O tempo necessário para que o pulso atravesse o enlace óptico é denominado
de tempo de retardo do sinal, o qual medido por unidade de comprimento
τ
1 δβ
representa o “atraso de grupo” ( τ g = =
=
).
L v g δw
SS= Dispersão do guia de onda
A dispersão de guia de onda (Dw) surge devido ao fato de que a velocidade de
grupo depende de λ.
∆τ = L Dw ∆λ
Dw é denominado de coeficiente de dispersão de guia de onda.
Dw =
1,984 N g 2
(2πa )2 2(cn 2 )2
, para 1,5 < ν < 2,4 . ν é freqüência normalizada.
A figura 5.24.1 mostra Dw versus λ (linha pontilhada).
SS=Dispersão de perfil
A velocidade de grupo do modo fundamental depende da diferença de índice
n
− n revest.
).
de refração normalizada ( ∆ = núcleo
nnúcleo
∆τ = L D p ∆λ , Dp é o coeficiente de dispersão de perfil, o qual é menor que 1
ps km-1 nm-1, e muito menor que Dm e Dw.
Na realidade a dispersão de perfil é um caso particular da dispersão material.
SS=Dispersão cromática
As dispersões que surgem nas fibras monomodos decorrem devido à estreita
largura espectral (∆λ) da fonte óptica. Podemos dizer que a dispersão
cromática é a somatória das dispersões material, de guia de onda, e de perfil.
∆τ = L (Dm + Dw + D p ) ∆λ = L (Dc ) ∆λ
Quando uma onda eletromagnética interage com os elétrons de um dielétrico, a
resposta do meio geralmente depende da freqüência da onda eletromagnética
(ω). Esta propriedade caracteriza a dispersão cromática, a qual se manifesta
devido à dependência do índice de refração n(ω) em relação à freqüência da
onda eletromagnética.
No nível fundamental, a origem da dispersão cromática está relacionada com
as características das freqüências de ressonância, nas quais o meio interage
com a radiação eletromagnética através das oscilações dos elétrons. Por outro
lado, o índice de refração pode ser calculado de forma aproximada através da
equação de Sellmeier mostrada abaixo:
1 + ∑ j =1 (β j ⋅ w j )
m
n (w ) =
2
w j − w2
ωj = freqüência de ressonância j
βj = Potência da ressonância j
A somatória da equação acima se estende sobre todos os materiais
ressonantes, que contribuem para a faixa de freqüência de interesse. No caso
das fibras ópticas, os pares βj e ωj são obtidos experimentalmente, através das
curvas de dispersão, de acordo com os constituintes do núcleo.
A dispersão na fibra ótica monomodo representa uma característica crítica na
propagação de pulsos óticos curtos, tendo em vista, que diferentes
componentes espectrais associados ao pulso viajam em diferentes velocidades
c
(
).
n (ω )
Mesmo em fibras óticas monomodo, quando os efeitos não lineares (devido à
dispersão induzida) não são importantes para o alargamento do pulso, a
dispersão cromática pode ser maléfica, para o desempenho do sistema de
comunicação óptico.
No regime não linear a contribuição da dispersão e da não linearidade pode
ocasionar diferentes comportamentos, conforme veremos mais à frente. Os
efeitos da dispersão na fibra óptica são relacionados através da expansão da
constante de propagação do modo (β) em uma série de Taylor, sobre a
freqüência central (ω0), conforme mostramos a seguir.
ω
1
1
β (ω ) = n (ω ) ⋅ = β 0 + (ω − ω0 ) ⋅ β1 + (ω − ω0 )2 ⋅ β 2 + (ω − ω0 )3 ⋅ β 3 + ...
c
2
6
n
d β 
; n = 0,1,2,3...
β n =  n 
d
ω

 (ω =ω )
0
O envelope do pulso óptico se move a uma velocidade v g =
1
β1
. O parâmetro
β2 é responsável pelo alargamento do pulso (dispersão de velocidade de grupo
(GVD)).
Observe na figura 5.25, a variação de n, e ng em relação ao comprimento de
onda λ, para fibras de sílica.
F= Figura 5.25 - Variação do índice de refração n, e do índice de refração de
grupo ng em relação ao comprimento de onda para fibras de sílica.
Comprimento de onda para GVD zero
É importante salientar, que β2 desaparece em torno do comprimento de onda
1,27µm, e torna-se negativo para comprimentos de onda maiores do que
1,27µm, conforme mostra a figura 5.26.
F= Figura 5.26 - Variação de β2 e d12 em relação ao comprimento de onda para
fibras de sílica. O parâmetro de dispersão β2 é igual a zero, próximo a λ =
1,27µm (1,312µm)
O comprimento de onda para β2 = 0 é denominado comprimento de onda de
dispersão de velocidade de grupo zero (λD). Entretanto, a dispersão não
desaparece totalmente neste comprimento de onda, pois em torno dele a
propagação do pulso está sujeita a inclusão do termo de terceira ordem na
equação de β(ω). Este efeito dispersivo de terceira ordem pode distorcer
pulsos óticos ultra curtos, tanto em regime linear, quanto em regime não linear,
porém a inclusão deste termo só é necessária, quando o comprimento de onda
do pulso se aproxima de λD.
O comportamento da dispersão das fibras ópticas atuais, geralmente se desvia
do valor apresentado anteriormente de 1,27µm, para 1,312µm, por duas
razões, sendo uma delas porque o núcleo da fibra ótica pode conter pequenas
quantidades de dopantes, tais como, GeO2 e P2O5.
SSS= Dispersão do guia de onda
Devido à propriedade dielétrica da fibra ótica, o índice efetivo de refração do
modo é ligeiramente menor do que o índice de refração material (n(ω)), sendo
esta redução dependente de ω. Isto resulta em uma contribuição do guia de
onda, denominada dispersão do guia de onda, a qual precisa ser adicionada à
dispersão cromática. Geralmente, a contribuição do guia de onda em relação a
β2 é desprezível, exceto próximo do comprimento de onda λD. O principal efeito
da contribuição do guia de onda é a segunda causa de um pequeno
deslocamento de λD no sentido dos comprimentos de onda maiores. Para fibra
óptica de sílica este deslocamento torna λD = 1,312µm, conforme já mostramos
anteriormente.
A figura 5.27 mostra a dispersão total medida em uma fibra óptica monomodo.
O parâmetro de dispersão D é usualmente utilizado na literatura sobre fibras
óticas, no lugar de β2, através da seguinte relação:
2
dβ1
 πc 
λ d n

D=
= − 2  ⋅ β 2 ≅ −  ⋅  2 
dλ
λ 
 c   dλ 
F= Figura 5.27 - Variação do parâmetro de dispersão D em relação ao
comprimento de onda para fibra óptica monomodo.
SSS= Regimes de dispersão Normal e Anormal
Para comprimentos de onda λ < λD resulta em β2 > 0, conforme você pode
constatar na figura acima, e neste caso a fibra óptica apresenta dispersão
normal. Em regime com dispersão normal, as componentes com freqüências
mais altas de um pulso óptico se propagam com velocidades menores do que
as componentes com freqüências mais baixas, diferentemente do que ocorre
em regime com dispersão anômalo (anormal), pois no regime de dispersão
anômalo, β2 < 0.
O regime de dispersão anômalo possui considerável interesse para o estudo
dos efeitos não lineares, tendo em vista que neste regime as fibras ópticas
podem suportar “solitons” através de uma ponderação entre os efeitos
dispersivos e não lineares.
SS= Dispersão de Polarização do Modo (PMD)
As fibras ópticas monomodo suportam apenas um modo (HE11), o qual se
consiste de dois modos com polarizações ortogonais. Apenas de forma ideal, o
núcleo de uma fibra óptica possui índice de refração uniforme em todas as
seções transversais. Entretanto, na realidade a anisotropia do índice de
refração pode ocorrer devido ao processo de fabricação (alterações na
composição da fibra óptica, e geometria, por exemplo, bem como devido aos
esforços aplicados às fibras ópticas, como, por exemplo, curvaturas. A
anisotropia do índice de refração ocasiona a propagação mais rápida de um
dos modos polarizados de forma ortogonal, em relação ao outro,
proporcionando a dispersão do pulso óptico, conforme mostra a figura 5.27.1
Figura 5.27.1 Dispersão de polarização de modo
Geralmente, a dispersão de polarização é menor que 1 ps km-1, e de forma
grosseira é função de L2.