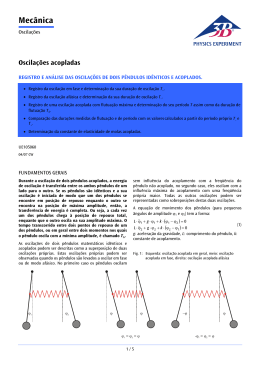
ONDAS PERÍODICAS
ELEMENTOS DE UMA ONDA:
COMPRIMENTO DE ONDA: Distância percorrida durante 1
oscilação completa!
MOVIMENTO HARMÔNICO
SIMPLES (MHS)
É um movimento periódico linear em torno de
uma posição de equilíbrio.
-A
A, -A: amplitude do MHS
0 é a posição de equilíbrio.
0
A
x  A. cos(.t  0 )
ω é a velocidade angular
Θ0 é a fase inicial.
EQUAÇÃO HORÁRIA DA VELOCIDADE
NO MHS
V  .Asen(.t  0 )
EQUAÇÃO HORÁRIA DA ACELERAÇÃO
NO MHS
a   . A cos(.t  0 )
2
Oscilações Mecânicas
Nosso mundo está repleto de oscilações, nas quais objetos se movem
repetidamente de um lado para outro. Muitas são simplesmente curiosas ou
desagradáveis, mas outras podem ser economicamente importantes ou perigosas.
Ex: Vento em linha de transmissão elétrica (linha “galopa”) podendo
rompê-lo;
Oscilação das asas do avião por causa da turbulência do ar;
Terremoto
Ponte de Tacoma
Ponte de
Tacoma
Ponte Rio
Niterói
Movimento Harmônico Simples (MHS)
É um movimento de oscilação repetitivo, ideal,
que não sofre amortecimento, ou seja, permanece
com a mesma amplitude ao longo do tempo.
MHS e (MCU) Movimento
Circular Uniforme
Movimento Harmônico Simples (MHS)
Cinemática do Movimento Harmônico Simples (MHS)
MassaMola
Deslocamento em função do tempo X(t)
x(t )  A. cos(.t   )
Fase inicial
Amplitude
Frequência
agular
Instante
1
f 
T
  2. . f
2

T

K
m
m
T  2
K
Cinemática do MHS
MassaMola
Velocidade em função do tempo v(t)
v(t )  . A.sen(.t   )
Amplitude
Frequência
agular
Fase inicial
Instante
1
f 
T
  2. . f
2

T

K
m
m
T  2
K
Movimento
Harmônico
Cinemática
do Simples
MHS (MHS)
MassaMola
Aceleração em função do tempo a(t)
a(t )   .A. cos(.t   )   .x(t )
2
Amplitude
2
Frequência
angular
Fase inicial
Instante
1
f 
T
  2. . f
2

T

K
m
m
T  2
K
Resumo – Cinemática do MHS
x(t )  A. cos(.t   )
v(t )  . A.sen(.t   )
a(t )   . A. cos(.t   )
2
Frequência
f 
1
T
  2. . f

2
T
Período

K
m
T  2
m
K
Constante
elástica da
mola
SISTEMA MASSA MOLA
m
T  2
k
k
f  1 / 2
m
ONDAS PERÍODICAS
• PERÍODO (T): tempo de uma oscilação completa;
• FREQUÊNCIA (f): número de oscilações completas
por segundo (Hz);
n
f 
t
1
f 
T
ESTUDO MATEMÁTICO DAS ONDAS
• VELOCIDADE DE PROPAGAÇÃO DE UMA ONDA
PERIÓDICA
Depende das condições do meio onda a Onda se propaga!
S
V
t
V

T
V = λ.f
COMPRIMENTO DE ONDA


Período (T)
O período de uma onda é o tempo que se demora para que uma onda
seja criada, ou seja, para que um comprimento de onda, ou um  ,
seja criado. O período é representado pela letra T.
Freqüência (f)
A freqüência representa quantas oscilações completas* uma onda dá
a cada segundo.
* Uma oscilação completa representa a passagem de um
comprimento de onda -  .
1
T
f
Física
Um pêndulo simples é um
sistema ideal que consiste de
uma partícula suspensa por um
fio inextensível e leve.
Quando afastado de sua posição
de equilíbrio e solto, o pêndulo
oscilará em um plano vertical
sob à ação da gravidade.
O movimento é periódico e
chama-se
período
de
oscilação (T) ao tempo gasto
para uma oscilação completa
(ida e volta).
fio inextensível
e sem massa
massa
pendular

L
Elementos do
pêndulo
simples:
L  comprimento
m
m  massa pendular
  amplitude
Período de oscilação para
pequenas amplitudes :

 ≤ 10°
L
T = 2..
m
L
g
Leis do pêndulo simples
1
O período de
oscilação não
depende da
amplitude (para
pequenas
amplitudes)
Período de oscilação para
pequenas amplitudes :
 ≤ 10°
T = 2..
L
g
Note que  não aparece na equação !
Leis do pêndulo simples
Período de oscilação para
pequenas amplitudes :
2
O período de
oscilação não
depende da massa
pendular.
T = 2..
L
g
Note que m não aparece na equação !
Leis do pêndulo simples
3
O período de
oscilação é
diretamente
proporcional à raiz
quadrada do
comprimento.
Período de oscilação para
pequenas amplitudes :
 ≤ 10°
T = 2..
L
g
Leis do pêndulo simples
4
O período de
oscilação é
inversamente
proporcional à raiz
quadrada
aceleração da
gravidade.
Período de oscilação para
pequenas amplitudes :
 ≤ 10°
T = 2..
L
g
Leis do pêndulo simples
5
O plano de
oscilação de um
pêndulo simples
permanece
constante.
Período de oscilação para
pequenas amplitudes :
 ≤ 10°
T = 2..
L
g
Leis do pêndulo simples
5
O plano de
oscilação de um
pêndulo simples
permanece
constante.
O plano de oscilação do
pêndulo abaixo permanece
constante, mesmo que o
suporte sofra rotação.
Principais
aplicações
pêndulo simples :
do
Comprovação do movimento de rotação
da Terra
Determinação
gravidade
da
aceleração
da
Comprovação do movimento de rotação
da Terra
Em 1600, Giordano Bruno foi
condenado à fogueira pela
Inquisição porque acreditava
que a Terra se movia em
torno do seu eixo e em torno
do Sol. Trinta e três anos
depois, Galileu Galilei só não
teve o mesmo destino
porque renunciou à sua
convicção científica.
A dificuldade em confirmar
a rotação da Terra reside no
fato de que se trata de uma
rotação muito lenta (0,0007
rotações por minuto).
Comprovação do movimento de rotação
da Terra
Em 1851, o astrônomo francês
Foucault realizou uma bela e
simples experiência capaz de
demonstrar a rotação da
Terra.
Com uma corda de 67 metros,
fixa no teto do Panteon de
Paris, ele suspendeu uma
esfera de ferro de 28 kg e
imprimiu-lhe um movimento
pendular.
Comprovação do movimento de rotação
da Terra
Na seqüência, o plano do
pêndulo passou a apresentar
uma lenta rotação no sentido
horário. Este movimento foi
facilmente explicado a partir
da suposição de que a Terra
gira em torno de seu eixo.
Comprovação do movimento de rotação
da Terra
Comportamento do
pêndulo de Foucault
No Pólo Norte o pêndulo dá uma
volta
completa a cada 24 horas
Em Paris o pêndulo completa
uma volta
a cada 31 horas e 47 min
No Equador não se percebe
movimento de rotação
Em 1851, eu
demonstrei o
movimento de
rotação da
Terra.
Jean Bernard
Leon Foucault
(1819-1868)
Determinação da aceleração da
gravidade
Para se determinar a aceleração da
gravidade em um ponto qualquer da
Terra basta dispor de um pêndulo
simples, um cronômetro e uma régua
(ou trena).
Determinação da aceleração da
gravidade
Com a régua (ou trena) mede-se o
comprimento do pêndulo  L
Com o cronômetro mede-se o período de
oscilação do pêndulo  T
T = 2..
L
g
isolando g
g = 4. 2
L
T2
Determinação da aceleração da
gravidade
Exemplo
Determinaremos a aceleração da gravidade onde um pêndulo de 1
metro oscila com um período de 2 segundos.
T = 2..
2 = 2..
L
g
1
g
g = 2
g = 3,142
g = 9,86 m/s2