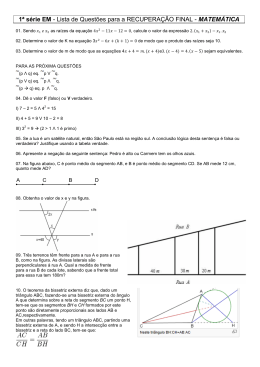
TRABALHO DE RECUPERAÇÃO DE MATEMÁTICA – 1° ENSINO MÉDIO
ALUNO: _________________________________________________ TURMA: __________
1) Qual é o valor numérico da expressão (a2 – x2) - (a2 + ax) para a = 2 e
x= -1?
2) Sendo A = 4x+3xy+8y e B = 6x – 5xy +4z, determine:
a) A + B
b) A – B
c) A.B
d) (A + B) – (A – B)
3) Fatore os seguintes polinômios:
a) x 2  3x
b) a 4  b 4
c) x 2  6 x  9
d ) x 2  8 x  15
4) Numa prova de Matemática o professor Pardal pediu que seus alunos
simplificassem a fração
x 2  2x
.
2x
O resultado corretamente obtido foi:
a) x2
b) x2 - 1
c) x - 1
d)
x2
2
(a  b) 2  (a  b).(a  b)  (a  b) 2
5) Simplificando a expressão:
obtemos:
9a 4  b 4
a)
1
3(a  b)(a  b)
b) 3a2 - b2
c)
1
3a  b 2
2
d) 3a2 + b2
6) Resolva as equações do 1º grau:
a )3 x  7  10
b)5 x  8  7 x  1
c)
3x  1 x  3

6
4
2
d )  12 x  3  3
7) Resolva as seguintes equações do 2º grau:
a) x2-6x+8 = 0
b) x2-4x+10 = 3x-2
c) x2 = x+6
d) (x2-7x+10)(2x+5) = 0
8) Resolva as biquadradas:
a ) x 4  8 x 2  16  0
b) x 4  4  3 x 2
9)
10)
11) Considere o triângulo retângulo ACE representado na figura a seguir cujos
lados têm as medidas indicadas.
C
a
e
A
c
E
Se Â, Ê, Ĉ são as medidas dos ângulos internos do triângulo, é correto afirmar que
senA. cos C
é igual a:
tgE
a)
c
a
b)
c
e
c)
e
a
d)
e
c
e)
a
e
12) (Vunesp) Um ciclista sobe, em linha reta, uma rampa com inclinação de 3
graus a uma velocidade constante de 4metros por segundo. A altura do topo da
rampa em relação ao ponto de partida é 30m.
Topo da
rampa
30m
3°
Ponto de partida

°
.
Calcule tempo em minutos, que o ciclista levou para percorrer completamente a
rampa. Use a aproximação sen 3° = 0,005.
13)
14) (FUVEST) A sombra de um poste vertical, projetada pelo sol sobre o chão
plano, mede 12m. Nesse mesmo instante, a sombra de um bastão vertical de
2m de altura mede 0,6m. Qual a altura do poste?
15) Em uma escola, o aluno deve obter média 6,0 em cada disciplina para ser
aprovado. Essa média é calculada dividindo-se o total de pontos que ele
obteve nos quatro bimestres, por quatro. Portanto, o aluno que não totalizar 24
pontos nos 4 bimestres deverá fazer prova final. Nessa prova, ele deverá obter,
no mínimo, a diferença entre 10,0 e a sua média anual, para ser aprovado.
As notas de Geografia de um certo aluno foram:
1º bimestre: 5,0
2º bimestre: 6,0
3º bimestre: 2,0
4º bimestre: 5,0
Logo, a nota mínima que esse aluno deverá obter na prova final de Geografia
é?
16) Comprei 5 doces a R$ 1,90 cada um, 3 doces a R$ 1,60 e 2 doces a R$
2,00 cada. O preço médio, por doce foi de?
17) Determine o domínio das seguintes funções:
a ) f ( x)  5 x  1
b) f ( x ) 
x
x 1
c) f ( x)  x  3
d ) f ( x) 
x
x3
18) Dada a função f(x) = 3x + 1, determine:
a) O Domínio da função
b) O ponto de intersecção com o eixo Y
c) O ponto de intersecção com o eixo X
d) O esboço do gráfico dessa função
19) Dada a função f(x) = x 2 - 2x – 8, determine:
a) O domínio da função
b) Os pontos de intersecção com os eixos X e Y
c) O gráfico da função
d) Os valores de x de modo que f(x) > 0
20) Tirando-se um certo valor de 775, obteve-se 496. Qual foi o percentual de
redução?
21) Qual é a taxa de juros mensais cobrada na venda de um aparelho de som, que
custa R$600,00 à vista, mas que será comprado em duas parcelas de $360,00,
sendo uma no ato e outra após 30 dias?
22) Maria tem duas opções para compra de um produto: sem juros em quatro
parcelas mensais de R$ 400,00; ou à vista, com 12% de desconto. Quanto irá
pagar, caso opte pelo pagamento à vista?
23) Calcular os juros simples do capital de R$ 680,00, colocado à taxa de 4% a.m.,
durante 1 ano.
24) Supondo que a taxa de juros de uma aplicação de R$ 2 000,00 seja de
15%a.a., quanto renderá, ao final de 5 anos, no regime de juros compostos?
25) Resolva as equações exponenciais:
a )5 x  125
b)4 x 1 
1
8
c)125 x  0,04
d ) 27 x
2
1
 95x
26) Resolva as seguintes equações: (Usar o artifício)
a )2 x 1  2 x  2 x 1  2 x  2  2 x  3  120
b) 4 x  6  2 x  8  0
27) Determine o valor dos seguintes logaritmos:
a ) log 2 64
b) log 1 81
9
c) log
125
25
d ) log 0, 25 32
28) Calcule o valor da expressão:
log 2 64  log 7 3 49
log 100  log 5 5 5
29) Sabendo que log 2 = 0,301; log 3 = 0,477; log 5 = 0,699 e log 7 = 0,845,
calcule:
a ) log
9
4
b) log 200
c ) log 72
d ) log 70
30) Interpolar 6 meios aritméticos entre 4 e 25.
31) Numa PA de dezessete termos, sabe-se que o quarto termo é 11 e o oitavo
termo é 23. Determine o 14º termo dessa PA.
32) Calcule a soma dos múltiplos de 3 compreendidos entre 4 e 98.
33) Encontre o vigésimo termo da progressão (2,6,18,...)
34) Calcule o número de termos da progressão (5,10,.....640)
NOME:_______________________________________________________________
TURMA; 1º
Nº___________
PROFESSOR (A): Samuel Mota
Trabalho de Física
NOTA: ______
Data de entrega: 09/12 /2015
INDICAR TODOS OS CÁLCULOS
Pressão e Densidade
2
1.
Aplica-se uma força de 80 N perpendicularmente a uma superfície de área 0,8 m . Calcule a pressão
exercida.
2.
Qual a pressão exercida por um tanque de água que pesa 1000 N, sobre a sua base que tem uma área de 2
2
m ?
3.
A água contida num tanque exerce uma pressão de 40 N/m2 sobre a sua base. Se a base tem uma área de
2
10 m , calcule a força exercida pela água sobre a base.
4.
Para pregar um prego numa parede, aplica-se uma martelada que transmite ao prego uma força de 50 N. A
2
área de contato da ponta do prego com a parede é de 0,2 mm .
Calcule a pressão exercida sobre a parede no instante da martelada.
5.
Uma pessoa cujo peso é 720 N está parada sobre o solo, apoiada nos dois pés. Admitindo que a área do
2
2
solado de cada um dos sapatos seja de 120 cm , qual a pressão, em N/m , que a pessoa exerce sobre o
solo?
6.
Três corpos de mesmo volume e aparência idêntica se encontram sobre uma mesa como ilustrado na
figura deste problema. Sendo d a densidade desses corpos, sabe-se que d1 < d2 < d3. Sobre a pressão p que
cada um destes corpos exerce sobre a mesa é correto afirmar que:
a) p1 = p2= p3;
b) p1 < p2 = p3;
c) p1 < p2 < p3;
d) p1 > p2 > p3;
e) p1 > p2 = p3
7.
3
Uma amostra de ouro tem 38,6 g de massa e 2 cm de volume. Outra amostra, esta de ferro, tem massa de
3
78 g e volume de 10 cm .
a) Determine as densidades do ouro e do ferro.
b) Dois corpos, maciços e homogêneos, de ouro e de ferro, respectivamente iguais, têm volumes iguais. Qual
apresenta maior massa?
c) Dois corpos, maciços e homogêneos, de ouro e de ferro, respectivamente, têm massas iguais. Qual apresenta
maior volume?
8.
Para se medir a pressão absoluta de um gás (p gás_abs) usa-se um manômetro, que consiste de um tubo em
forma de U contendo Hg (=13,6x10 kg/m ). Com base na figura, e sendo a pressão atmosférica
5
2
2
patm=1,0x10 N/m , determine pgás_abs. Considere a aceleração da gravidade local g=9,8m/s .
3
9.
3
A figura mostra três vasos V1, V2 e V3 cujas bases têm a mesma área. Os vasos estão cheios de líquidos l 1, l2
e l3 até uma mesma altura. As pressões no fundo dos vasos são P 1, P2 e P3, respectivamente. Com relação a
essa situação é correto afirmar que:
a) P1 = P2= P3 somente se os líquidos l1, l2 e l3 forem idênticos.
b) P1 = P2= P3 quaisquer que sejam os líquidos l 1, l2 e l3 .
c) P1 > P2> P3 somente se os líquidos l1, l2 e l3 forem idênticos
d) P1 > P2> P3 quaisquer que sejam os líquidos l 1, l2 e l3 .
10. O tubo aberto em forma de U da figura contém dois líquidos não miscíveis, A e B, em equilíbrio. As alturas
das colunas de A e B, medidas em relação à linha de separação dos dois líquidos, valem 50cm e 80cm,
respectivamente.
3
3
a) Sabendo que a massa específica de A é 2.10 kg/m , determine a massa específica do líquido B.
2
5
2
b) Considerando g=9,8m/s e a pressão atmosférica igual a 1.10 N/m , determine a pressão absoluta no interior do
tubo na altura da linha de separação dos dois líquidos.
5
2
2
11. Num local onde a pressão atmosférica é patm = 10 N/m e a aceleração da gravidade é g = 10 m/s , uma
pessoa mergulha até o fundo de um lago cuja profundidade é H = 10 m. Qual a pressão sustentada por essa
3
3
pessoa no fundo do lago? A densidade da água é d = 10 kg/m .
3
12. Deseja-se construir uma prensa hidráulica que permita exercer no êmbolo maior uma força de 5,0 x 10 N,
2
quando se aplica uma força de 5,0 x 10 N no êmbolo menor, cuja área é de 2,0 x 10 cm . Nesse caso qual
deverá ser a área do êmbolo maior ?
13. As áreas dos pistões do dispositivo hidráulico da figura mantêm a relação 50:2. Verifica-se que um peso P,
colocado sobre o pistão maior é equilibrado por uma força de 30 N no pistão menor, sem que o nível de
fluido nas duas colunas se altere. De acordo com o princípio de Pascal, o peso P vale:
14. Na prensa hidráulica mostrada na figura, os diâmetros dos tubos 1 e 2 são, respectivamente, 4cm e 20cm.
Sendo o peso do carro igual a 10000N, determine:
a) a força que deve ser aplicada no tubo 1 para equilibrar o carro.
b) o deslocamento do nível de óleo no tubo 1, quando o carro sobe 20cm.