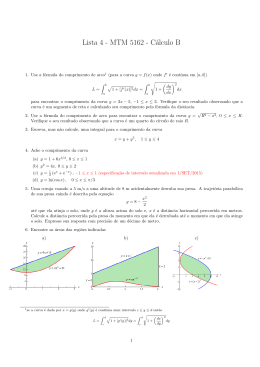
Mecânica e Ondas
fascı́culo 23
May 27, 2008
Contents
23.1
23.2
23.3
23.4
23.5
Oscilações acopladas . . . . .
Conceito de onda . . . . . . .
Equação das cordas vibrantes
Intensidade de uma onda . .
Modos normais de vibração .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Mario J. Pinheiro
Departamento de Fı́sica e Instituto de Plasmas e Fusão Nuclear
Instituto Superior Técnico
email: [email protected]
413
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
414
420
421
422
423
“O homem vulgar, por mais dura que lhe seja a vida, tem ao menos
a felicidade de a não pensar. Viver a vida decorrentemente, exteriormente, como um gato ou um cão - assim fazem os homens gerais,
e assim se deve viver a vida para que possa contar a satisfação do
gato e do cão. Pensar é destruir. O próprio processo do pensamento
o indica para o mesmo pensamento, porque pensar é decompor. Se os
homens soubessem meditar no mistério da vida, se soubessem sentir as mil complexidades que espiam a alma em cada pormenor da
acção, não agiriam nunca, não viveriam até. Matar-se-iam assustados, como os que se suicidam para não ser guilhotinados no dia
seguinte.”
- Fernando Pessoa, in “O Livro do Desassossego”
23.1
Oscilações acopladas
Consideremos um sistema de dois pêndulos acoplados com o mesmo comprimento l e massa m, ligados por uma mola de constante elástica k e sujeitos a
oscilar no plano vertical definido pelas suas posições de equilı́brio (Fig. 1). O
sistema tem dois graus de liberdade.
Sejam x1 e x2 os deslocamentos das duas partı́culas suspensas em relação à
posição de equilı́brio e que por hipótese sejam suficientemente pequenos para
que se possam confundir os arcos com as cordas, x1 ≈ lθ1 e x2 ≈ lθ2 . A
mola deforma-se com o alongamento x2 − x1 , supostamente positiva, tal como
se apresenta na Fig. 1 e donde se pode concluir que terá que resultar a força
k(x2 − x1 ) para a direita agindo sobre a partı́cula 1 e −k(x2 − x1 ) (para a
esquerda) agindo sobre a partı́cula 2. As duas massas encontram-ser igualmente
sujeitas às forças gravı́ticas com as componentes tangenciais respectivas:
x1
x2
= −ωo2 x1 −mg sin θ2 ≈ −mgθ2 = −mg
= −ωo2 x2
l
l
(23.1)
p
onde ωo = gl . Desprezando qualquer tipo de amortecimento, temos
−mg sin θ1 ≈ −mgθ1 = −mg
mẍ1 = −mωo2 x1 + k(x2 − x1 )
mẍ2 = −mωo2 x2 − k(x2 − x1 )
Pondo
K=
k
m
(23.2)
(23.3)
e dividindo as Eqs. 23.2 por m, obtemos
ẍ1 + ωo2 x1 = K(x2 − x1 )
ẍ2 + ωo2 x2 = K(x2 − x1 )
414
(23.4)
Neste caso podemos desacoplar as duas equações. Somando membro a membro,
obtemos primeiro
(ẍ1 + ẍ2 ) + ωo2 (x1 + x2 ) = 0
(23.5)
Subtraindo as mesmas Eqs. 23.4, obtemos
(ẍ1 − ẍ2 ) + ωo2 (x1 − x2 ) = 2K(x1 − x2 )
(23.6)
Se escolhermos um novo tipo de variáveis, tais como,
q1 = 12 (x1 + x2 )
q2 = 12 (x1 − x2 )
(23.7)
q̈1 + ωo2 q1 = 0
q̈2 + ω22 q2 = 0
(23.8)
As Eqs. 23.4 ficam na forma
onde
ω2 =
p
ωo2 + 2K
(23.9)
e cujas soluções são
q1 (t) = A1 cos(ωo t + δ1 )
q2 (t) = A2 cos(ω2 t + δ2 )
(23.10)
É fácil confirmar que x1 e x2 são dados em função deste q’s:
x1 (t) = q1 (t) + q2 (t)
x2 (t) = q1 (t) − q2 (t).
(23.11)
As coordenadas q1 e q2 , como verificámos, oscilam harmonicamente e chamamos
coordenadas normais. Com elas o sistema fica desacoplado e podemos ver
sem dificuldade que q1 corresponde ao deslocamento do centro de massa, enquanto que 2q2 = x1 − x2 corresponde ao deslocamento relativo entre as duas
partı́culas.
Se escolhermos apropriadamente as condições iniciais, tais como:
A2 = 0 Corresponde a q1 (t) = A1 cos(ωo t+δ1 ) = x1 (t) = x2 (t). O deslocamento
dos dois pêndulos são iguais, é o chamado modo simétrico e como a mola
não é deformada, tudo se passa como se ela não existisse e cada pêndulo
oscila com a sua frequência livre ωo (Fig. 1-(b)).
A1 = 0 Corresponde a q2 (t) = x1 (t) = A2 cos(ω2 t + δ2 ) = −x2 (t). O deslocamento dos dois pêndulos são iguais e contrários sendo chamado de modo
assimétrico. Como a força restauradora da mola aparece, a frequência
de oscilação é mais elevada, ω2 > ωo (Fig. 1-(c)).
415
Figure 1: (a) Sistema de dois pêndulos acoplados; (b) modo simétrico; (c) modo
antissimétrico.
416
As condições iniciais para o modo simétrico correspondem ao mesmo deslocamento inicial e à mesma celocidade inicial:
x10 = x20
ẋ10 = ẋ20
(23.12)
No modo antisimétrico temos deslocamentos e velocidades iniciais contrárias:
x10 = −x20
ẋ10 = −ẋ20
(23.13)
Em particular podemos analisar o que se passa se deslocarmos apenas um dos
pêndulos da posição de equilı́brio, deixando o outro no repouso:
x10 = a; x20 = 0; ẋ10 = ẋ20 = 0.
(23.14)
As condições iniciais para as coordenadas normais são:
q10 = q20 =
a
; q̇10 = q̇20 = 0
2
(23.15)
Como se pode ver rapidamente, as soluções gerais dão
δ1 = δ2 = 0;
A1 = A2 = a2 .
(23.16)
ou seja, obtemos como solução duas superposições de mesma amplitude e
frequência diferentes:
x1 (t) = a2 [cos(ωo t) + cos(ω2 t)]
x2 (t) = a2 [cos(ωo t) − cos(ω2 t)]
(23.17)
Se definirmos uma frequência angular média:
ω≡
1
(ωo + ω2 )
2
(23.18)
e as diferenças de frequências
∆ω ≡ ωo − ω2
(23.19)
podemos reescrever as Eqs. 23.17 na forma
x1 (t) = a cos( ∆ω
2 t) cos(ωt)
x2 (t) = a sin( ∆ω
2 t) sin(ωt)
(23.20)
No caso limite do acoplamento fraco, quando a força restauradora é pequena,
verifica-se
K ¿ ωo2 ; ∆ω ¿ ω.
(23.21)
As soluções correspondem ao fenómeno de batimentos, onde x1 é modulado
∆ω
por cos ∆ω
2 t e X2 é modulado por sin( 2 t) (Fig. 2).
417
Figure 2: Fenómeno de batimentos.
Figure 3: Duas massas unidas por três molas elásticas a duas paredes fixas.
Exemplo 1: Osciladores acoplados longitudinais: Duas massas iguais estão
ligadas por meio de molas entre si e a duas extremidades fixas, segundo a mesma
direcção (como mostra a Fig. 3). As molas que ligam as massas às extremidades
têm constante de restituição k e a mola que liga as duas massas tem constante
k0 .
a) Escreva o lagrangeano do sistema: [Sugestão: escolha como coordenadas
generalizadas os deslocamentos das massas em relação às suas posições de
equilı́brio.]
L=K −U =
K = 21 m1 ẋ21 + 12 m2 ẋ22
1
U = 2 kx21 + 12 k 0 (x1 − x2 )2 + 21 kx22
1
1
1
1 0
2
2
2
2 m1 ẋ1 + 2 m2 ẋ2 − 2 kx1 − 2 k (x1 −
b) Determine as equações do movimento.
QuadroNegro 1
418
(23.22)
x2 )2 − 12 kx22
Exemplo 2: Um corpo de 2 kg oscila preso a certa mola com a constante de
força k = 400 N/m. A constante de amortecimento tem o valor b = 2.00 kg/s.
O sistema é excitado por uma força sinusoidal cujo valor máximo é de 10 N e
a frequência angular ω = 10 rad/s. (a) Qual a amplitude da oscilação? (b) Se
a frequência de excitação variar, em que frequência ocorrerá a ressonância? (c)
Qual a amplitude das oscilações
Os dados numéricos são os seguintes:
m = 2kg
k = 400N/m
b = 2.00kg/s
Fo = 10N
ω = 10rad/s
(23.23)
A equação do movimento é a seguinte:
P
2
Fx = max = m ddt2x = −kx − bv + Fo cos ωt
2
2
∴ m ddt2x + b dx
dt + mωo x = Fo cos ωt
(23.24)
A solução é do tipo:
x = xtrans + xperm
xperm = A cos(ωt − δ)
A = √ 2 2 Fo 2 2 2
m (ωo −ω )+b ω
tan δ = m(ωbω
2
2
o −ω )
QuadroNegro 2
419
(23.25)
23.2
Conceito de onda
Uma onda é qualquer sinal que se tranmite de um ponto a outro de um meio
com velocidade definida. As ondas podem ser transversais (ex: onda electromagnéticas) ou longitudinais (ex: ondas sonoras).
Vamos abordar o caso mais simples da propagação de uma onda a 1 dimensão,
por exemplo, ondas transversais numa corda com amplitude y(x, t). A forma
geral de uma onda progressiva que se desloca nos dois sentidos do eixo Ox (onda
a uma dimensão) com velocidade constante v é do tipo:
y(x, t) = f (x − vt) + g(x + vt),
(23.26)
onde f e g representam funções arbitrárias de x e t.
Uma onda harmónica tem a forma
f (x0 ) = A cos(kx0 + δ)
(23.27)
onde f (x0 ) representa uma perturbação num ponto x0 , que corresponde a um
referencial que acompanha a onda. Se quisermos passar para um referencial que
está fixo no espaço, teremos que aplicar as transformações de Galileu, para uma
onda progressiva que se desloca para a direita será x0 = x − vt, e a amplitude
da onda neste referencial fixo passará a ser
y(x, t) = A cos[k(x − vt) + δ].
Mas havendo a relação
ω = kv = 2πν =
2π
τ
(23.28)
(23.29)
e substituindo na Eq. 23.28, temos
y(x, t) = A cos(kx − ωt + δ).
(23.30)
O argumento do coseno é a fase da onda:
ϕ(x, t) = kx − ωt + δ
(23.31)
e δ a constante de fase. Se acompanharmos o deslocamento da onda com o
tempo de modo a que a fase ϕ se mantenha constante, obtemos
dϕ
dx
=k
− ω = 0,
dt
dt
(23.32)
obtendo-se finalmente a velocidade de fase, v:
ω
dx
= = v = νλ.
dt
k
(23.33)
A frequência ν = 1/τ dá o número de oscilações por unidade de tempo, e
σ = 1/λ dá o número de comprimentos de onda por unidade de comprimento,
chamando-se número de onda.
420
A equação de ondas unidimensional é uma das equações mais fundamentais da
fı́sica e tem a forma:
1 ∂2y
∂2y
−
= 0.
(23.34)
2
v ∂t
∂x2
É uma equação a derivadas parciais linear de segunda ordem.
23.3
Equação das cordas vibrantes
Seja µ a densidade linear de massa da corda. Um elemento infinitesimal de
comprimento ∆x tem a massa ∆m = µ∆x.
Vamos considerar um deslocamento transversal de pequena magnitude de um
ponto x da corda da sua posição de equilı́brio e designar a sua nova posição por
y(x, t). Nesta aproximação vamos considerar praticamente constante o comprimento da corda assim como as tensões exercidas sobre ela em dois pontos x
e x + ∆x. As forças exercidas serão assim devidas unicamente à variação da
direcção da tensão, introduzindo uma força restauradora ao longo de Oy.
Vê-se na Fig. ?? que no ponto x + ∆x a componente em y da tensão é
T sin θ ≈ T tan θ = T
∂y
.
∂x
(23.35)
O ângulo θ é o ângulo entre a tangente à corda e o eixo Ox e usámos a aproximação sin θ ≈ tan θ válida para pequenos ângulos θ ¿ 1. Recordamos que
tan θ = ∂y/∂x.
A força vertical resultante que actua sobre o elemento ∆x da corda é dada por
∂y
T
(x + ∆x, t) −
∂y
∂y
(x + ∆x, t) − T
(x, t) = T ∆x[ ∂x
∂x
∂x
∆x
∂y
∂x (x, t)
].
(23.36)
Podemos agora usar uma expansão em série de Taylor:
∂f
1
∂2f
1
∂nf
)o + (x − xo )2 ( 2 )o + ... + (x − xo )n ( 2 )o + ...
∂x
2!
∂x
n!
∂x
(23.37)
que, neste caso, se ∆x ¿ 1, podemos escrever (tente fazer)
f (x) = f (xo ) + (x − xo )(
∂y
∂2y
∂y
(x + ∆x) ≈ ( )(x, t) + ∆x( 2 )
∂x
∂x
∂x
Substituindo a Eq. 23.38 na Eq. 23.36, obtemos
QuadroNegro 3
421
(23.38)
Chegamos finalmente à equação das cordas vibrantes unidimensional
µ
∂2y
∂2y
=T 2
2
∂t
∂x
onde a velocidade de propagação da onda transversal é
s
T
.
v=
µ
23.4
(23.39)
(23.40)
Intensidade de uma onda
Uma onda progressiva transporta energia, podendo em particular ser transmitida a uma partı́cula colocada na extremidade da corda. A força transversal
actuando sobre um elemento da corda no ponto x é dada por
Fy = −T
∂y
(x, t).
∂x
(23.41)
O trabalho realizado sobre o elemento da corda por unidade de tempo é dado
pelo produto da força pela velocidade:
P (x, t) = Fy
∂y
∂y ∂y
= −T
.
∂t
∂x ∂t
(23.42)
Para uma onda harmónica temos
∂y
∂x = −kA sin ϕ
∂y
∂t = ωA sin ϕ
(23.43)
P (x, t) = ωkT A2 sin2 (kx − ωt + δ).
(23.44)
A potência é dada por
À média sobre um perı́odo chamamos intensidade I da onda. Ela é facilmente
obtida fazendo a média temporal do temos sinusoidal ao quadrado, que já vimos
em fascı́culo anterior que vale 1/2:
I =< P >= P =
1
ωkT A2 .
2
(23.45)
Como já vimos, T = µv 2 e ω = kv, e a intensidade da onda também se pode
escrever
1
I = P = µνω 2 A2 .
(23.46)
2
A intensidade da onda é proporcional ao quadrado da amplitude, à velocidade
da onda e ao quadrado da frequência.
422
23.5
Modos normais de vibração
Consideremos agora uma corda vibrante de comprimento finito l com as extremidades presas. Vamos procurar os modos normais de vibração da corda,
isto é, o modo de oscilação em que todos os elementos da corda oscilam com a
mesma frequência ω e a mesma constante de fase δ, embora cada ponto x possa
naturalmente deslocar-se com amplitude A(x) diferente de ponto para ponto.
Isto é, consideremos uma onda estacionária:
(23.47)
y(x, t) = A(x) cos(ωt + δ)
Verifica-se rapidamente que
2
1 ∂ y
ω2
v 2 ∂t22 = − v 2 A(x) cos(ωt +
∂ y
d2 A
∂t2 = dx2 cos(ωt + δ)
ou seja
δ)
(23.48)
d2 A
+ k 2 A(x) = 0
dx2
(23.49)
A(x) = a cos(kx) + b sin(kx)
(23.50)
cuja solução geral é da forma
A condição de que as duas extremidades permaneçam fixas é dada pela condição
de contorno:
y(0, t) = y(l, t) = 0, ∀t.
(23.51)
Esta relação implica que temos que ter também
A(0) = a = 0
A(l) = b sin(kl) = 0
(23.52)
Atendendo a que b 6= 0 forçosamente (de outro modo seria tudo nulo), concluı́mos que esta condição só pode ser satisfeita para valores discretos da
variaável k:
nπ
kn =
(23.53)
l
onde n = 1, 2, 3, .... As frequências dos modos normais de vibração são
ωn = kn v =
nπ
v
l
(23.54)
e a expressão dos modos normais de vibração é dada por
yn (x, t) = bn sin(kn x) cos(ωn t + δn ).
(23.55)
O comprimento de onda associado λn associado ao modo n é
λn =
2π
2l
= .
kn
n
423
(23.56)
Figure 4: (a) Modos de vibração de uma corda vibrante. (b) Escala harmónica
em notação musical.
A frequência νn do modo n é
νn =
ωn
v
= n = nν1
2π
2l
(23.57)
q
v
1
T
onde ν1 = 2l
= 2l
µ é a frequência do modo fundamental. As frequências da
corda vibrante são múltiplos inteiros da frequência ν1 do modo fundamental.
Exemplo 3: Duas ondas transversais de mesma frequência ν = 100 s−1 são
produzidas num fio de aço de 1 mm de diâmetro e densidade ρ = 8 g/cm3 ,
submetido a uma tensão T = 500 N. As ondas são dadas por
y1 = A cos(kx − ωt + π6 )
y2 = 2A sin(ωt − kx).
onde A = 2 mm. (a) Escreva a expressão da onda harmónica progressiva resultante da superposição das duas ondas. (b) Calcule a intensidade da resultante.
(c) Se fizermos variar a diferença de fase entre as duas ondas, qual é a razão
entre os valores máximo e mı́nimo possı́veis da intensidade da resultante?
424
Os dados que temos permitem obter:
ν = 100s−1 s = 100Hz.
ω = 2πν = 628rad/s.
2
µ = ρA = ρπ( D
2)
−3
kg/m
q
q µ = 2π10
∴v=
T
µ
⇒k=
=
ω
v
=
500
2π10−3
628
282.1 =
= 282.1m/s
2.23m−1 .
É conveniente usarmos números complexos z = Aei(ωt+δ) . A parte real do
número complexo é dada por
y(t) = <z(t) = <[Aei(ωt−kx+δ) ] = A cos(ωt − kx + δ)
(23.58)
A superposição dos dois movimentos consiste no seu somatório. Iremos somar
as quantidades complexas respectivas:
y = y1 + y2
π
⇒ z = z1 + z2 = Aei(kx−ωt+ 6 ) + 2Aei(ωt−kx)
(23.59)
Podemos verificar em tabelas trigonométricas os eguintes resultados:
sin θ = cos(θ√+ π2 )
cos π6 = 23
sin π6 = 12
iφ
e = cos φ + i sin φ
(23.60)
Um número complexo pode-se colocar na forma
z = x + iy = r(cos φ + i sin φ) = reiφ − f ormap
− trigonometrica − do − numero − complexo
r =| z |= x2 + y 2
φ = Argz = arctan( xy )
(23.61)
Com estes dados podemos reescrever as duas Eqs. 23.60 na forma mais conveniente
y = A cos(kx − ωt + π6 ) + 2A sin[−(kx − ωt)]
y = A cos(kx − ωt + π6 ) + 2A cos(kx − ωt + π2 )
π
π
z = Aei(kx−ωt+ 6 ) + 2Aei(kx−ωt+ 2 )
π
π
(23.62)
z = Aei(kx−ωt) [e√i 6 + 2ei( 2 ) ]
z = Aei(kx−ωt) [√23 + i 12 + 2i]
z = Aeiφ [ 23 + 52 i]
onde φ = kx − ωt. Podemos escrever a última expressão dentro do parentesis
recto na forma
√
3 5
+ i] = reiδ
zc = [
(23.63)
2
2
O seu módulo é
√
| zc |= r = A 7
(23.64)
425
enquanto que o argumento de zc calcula-se através da fórmula
y
= arctan
x
5
√2
3
2
5
= arctan √ = 1.237rad = 70.89o .
3
(23.65)
Finalmente, podemos escrever a resultante das duas vibrações:
δ = Argzc = arctan
y = <z = Arei(φ+δ)
y = 5.20 × 10−3 cos(kx − ωt + 1.237).
(23.66)
b) A intensidade resultante é dada por
I = 12 6.28 × 10−3
I = (y1 + y2 )2
1
2 2
qI = 2 µνω A
500
2
6.28×10−3 (2π100) (5.29
× 10−3 )2
(23.67)
I = 9.79W
c) Intensidade resultante é calculada usando o seguinte resultado (aqui dado
sem demonstração). Se duas vibrações têm a mesma frequência angular, tal que
x1 (t) = A1 cos(ωt + φ1 )
x2 (t) = A2 cos(ωt + φ2 )
(23.68)
então a magnitude A da resultante é dada pela expressão:
A2 = A21 + A22 + 2A1 A2 cos(φ2 − φ1 )
(23.69)
Verificamos de imediato que os máximos da intensidade (que é proporcional ao
quadrado da amplitude) correspondem a
δ12 ≡ φ2 − φ1 = 2nπ(n = 0, ±1, ±2, ...)
∴ Imax ∝ (A1 + A2 )2
(23.70)
enquanto que os seus mı́nimos correspondem a
δ12 = (2n + 1)π
∴ Imin ∝ (A1 − A2 )2
(23.71)
O seu rácio é:
R=
Imax
(A1 + A2 )2
(A + 2A)
(3A)2
=
=
=
= 9.
Imin
(A1 − A2 )2
A − 2A
A2
426
(23.72)