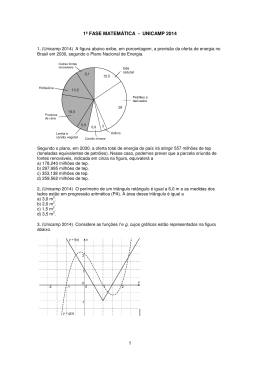
PROVA DE MATEMÁTICA DO VESTIBULAR 2013
DA UNICAMP-FASE 1.
RESOLUÇÃO: PROFA. MARIA ANTÔNIA C. GOUVEIA
QUESTÃO 37
A figura abaixo exibe, em porcentagem, a previsão da oferta de energia no Brasil em 2030,
segundo o Plano Nacional de Energia.
Segundo o plano, em 2030, a oferta total de energia do país irá atingir 557 milhões de tep
(toneladas equivalentes de petróleo). Nesse caso, podemos prever que a parcela oriunda de
fontes renováveis, indicada em cinza na figura, equivalerá a
a) 178,240 milhões de tep.
b) 297,995 milhões de tep.
c) 353,138 milhões de tep.
d) 259,562 milhões de tep.
RESOLUÇÃO:
46,6% de 557 milhões de tep = 0,466  557 milhões de tep = 259,562 milhões de tep.
RESPOSTA: Alternativa d.
QUESTÃO 38
Um investidor dispõe de R$ 200,00 por mês para adquirir o maior número possível de ações de
certa empresa. No primeiro mês, o preço de cada ação era R$ 9,00. No segundo mês houve
uma desvalorização e esse preço caiu para R$ 7,00. No terceiro mês, com o preço unitário das
ações a R$ 8,00, o investidor resolveu vender o total de ações que possuía. Sabendo que só é
permitida a
negociação de um número inteiro de ações, podemos concluir que com a compra e venda de
ações o investidor teve
a) lucro de R$ 6,00.
b) nem lucro nem prejuízo.
c) prejuízo de R$ 6,00.
d) lucro de R$ 6,50.
1
RESOLUÇÃO:
Primeiro mês: Sendo, 200 = 9  22 + 2 = 198 + 2, foram compradas 22 ações a 9 reais cada
uma, numa despesa total de 198 reais.
Segundo mês: Sendo, 200 = 7  28 + 4 = 196 + 4, foram compradas 28 ações a 7 reais cada
uma, numa despesa total de 196 reais.
DESPESA TOTAL com a compra das ações: 198 + 196 = 394 reais.
Terceiro mês: Vendeu 22 + 28 = 50 ações a 8 reais cada uma. A receita do investidor com a
venda das ações foi 50  8 = 400 reais.
Um lucro de 400 – 394 = 6
RESPOSTA: Alternativa a.
QUESTÃO 39
O perímetro de um triângulo retângulo é igual a 6,0 m e as medidas dos lados estão em
progressão aritmética (PA). A área desse triângulo é igual a
2
2
2
2
a) 3,0 m .
b) 2,0 m .
c) 1,5 m .
d) 3,5 m .
RESOLUÇÃO:
Representando as medidas dos lados do triângulo como a – r, a e a + r (as medidas dos lados
estão em progressão aritmética).
Como seu perímetro é 6,0m, a – r + a + a + r = 6  3a = 6  a = 2.
Então os lados medem 2 – r, 2 e 2 + r.
2
2
(2 + r) = (2 – r) + 4  4 + 4r = 4 – 4r + 4  8r = 4  r = 0,5
Então os lados medem 1,5m, 2m e 2,5m.
A área do triângulo em metros quadrados é (2  1,5) : 2 = 1,5.
RESPOSTA: Alternativa c.
QUESTÃO 40
Um caixa eletrônico de certo banco dispõe apenas de cédulas de 20 e 50 reais. No caso de um
saque de 400 reais, a probabilidade do número de cédulas entregues ser ímpar é igual a
a) 1/4.
b) 2/5.
c) 2/3.
d) 3/5.
RESOLUÇÃO:
O saque poderá ser feito dos seguintes modos: 20 notas de 20 reais; 15 notas de 20 reais mais
2 notas de 50 reais; 10 notas de 20 reais mais 4 notas de 50 reais; 5 notas de 20 reais mais 6
notas de 50 reais; 8 notas de 50 reais.
Então o número de cédulas entregues pode ser: 20, 17, 14, 11 e 8.
A probabilidade do número de cédulas entregues ser ímpar é igual a 2/5.
RESPOSTA: Alternativa b.
2
QUESTÃO 41
Considere as funções f e g, cujos gráficos estão representados na figura abaixo.
O valor de f(g(1)) – g(f(1)) é igual a
a) 0.
b) -1.
c) 2.
d) 1.
RESOLUÇÃO:
g(1) = 0; f(g(1)) = f(0) = 1.
f(1) = 1; g(f(1)) = g(1) = 0.
f(g(1)) – g(f(1)) = 1 – 0 = 1.
RESPOSTA: Alternativa d.
QUESTÃO 42
Seja real tal que cos x  tan x . O valor de senx é
a) ( 3  1) / 2 .
b) (1  3 ) / 2 .
c) ( 5  1) / 2 .
d) (1  5 ) / 2 .
RESOLUÇÃO:
senx

cos x
Analisando o círculo trigonométrico ao lado, conclui-se que x é
o
o
um arco de 1 ou de 2 quadrante, logo o seu seno é um número
positivo.
cos x  tan x  cos x 
cos x 
senx
 cos 2 x  senx  1  sen 2 x  senx  sen 2 x  senx  1  0 
cos x
senx 
1 1 4
1 5
1 5
 senx 
 senx 

2
2
2
5 1
2
RESPOSTA: Alternativa c.
3
QUESTÃO 43
A razão entre a idade de Pedro e a de seu pai é igual a 2/9.
Se a soma das duas idades é igual a 55 anos, então Pedro tem
a) 12 anos.
b) 13 anos.
c) 10 anos.
d) 15 anos.
RESOLUÇÃO:
De acordo com os dados da questão e sendo x a idade de Pedro e y a idade de seu pai,
9x

x 2
y

2 x  9 x  110
 

2
tem-se o sistema:  y 9


 x  y  55  x  9 x  55  x  10


2

RESPOSTA: Alternativa c.
QUESTÃO 44
No plano cartesiano, a reta de equação 2x – 3y =12 intercepta os eixos coordenados nos
pontos A e B. O ponto médio do segmento AB tem coordenadas
a) (4, 4/3).
b) (3, 2).
c) (4, 4/3).
d) (3, 2).
RESOLUÇÃO:
A reta de equação 2x – 3y =12 intercepta o eixo dos x no ponto A = (x, 0) e o eixo dos y no
ponto B = (0,y).
Se y = 0, 2x =12  x = 6  A = (6, 0).
Se x = 0, – 3y =12  y = – 4 B= (0, – 4).
6 4
O ponto médio do segmento AB tem coordenadas,  ,
  3,2 .
2 2 
RESPOSTA: Alternativa d.
QUESTÃO 45
Considere um cilindro circular reto. Se o raio da base for reduzido pela metade e a altura for
duplicada, o volume do cilindro
a) é reduzido em 50%.
b) aumenta em 50%.
c) permanece o mesmo.
d) é reduzido em 25%.
RESOLUÇÃO:
Considere-se um cilindro de raio r e altura h. O volume desse cilindro é V  r 2 h.
Considere-se agora um cilindro de raio 0,5r e altura 2h. O volume desse cilindro é
V1   (0,5r ) 2 .2h   (0,25r 2 ).2h  0,5r 2 h .
Comparando V e V1, conclui-se que V1 é a metade de V.
RESPOSTA: Alternativa a.
4
QUESTÃO 46
O gráfico abaixo exibe a curva de potencial biótico q(t ) para uma população de microorganismos, ao longo do tempo .
Sendo a e b constantes reais, a função que pode representar esse potencial é
a) q(t) = at + b.
b) q(t) = abt.
c) q(t) = at² + bt.
d) q(t) = a + logbt .
RESOLUÇÃO:
A função q(t) = at + b é uma função linear e a função q(t) = at² + bt é uma função quadrática
com q(0) = 0.
Então a função que pode representar esse potencial é a função exponencial q(t) = abt.
RESPOSTA: Alternativa b.
QUESTÃO 47
O módulo do número complexo z  i 2014  i1987 é igual a
a)
2.
b) 0.
c)
3 .
d) 1.
RESOLUÇÃO:
i0  1; i1  i; 12  1; i3  i; i 4  1; i5  i 4 .i  i; i6  i 4 .i 2  1.(1)  1;....
i 2014  12012.i 2  i 4 .i 2  1(1)  1
i1987  11984.i 3  1.(i)  i .
z  i 2014  i1987  1  i  z  1  i  z  1  1  2 .
RESPOSTA: Alternativa a.
5
QUESTÃO 48
1 a 1


Considere a matriz M   b 1 a  , onde a e b são números reais distintos. Podemos afirmar
1 b 1


que
a) a matriz M não é invertível.
b) o determinante de M é positivo.
c) o determinante de M é igual a a²  b².
d) a matriz M é igual à sua transposta
RESOLUÇÃO:
1 a 1
det M  b 1 a  1  b 2  a 2  1  ab  ab  b 2  a 2  2ab  (a  b) 2  0, porque
1 b 1
a e b são números reais diferentes.
RESPOSTA: Alternativa b.
6