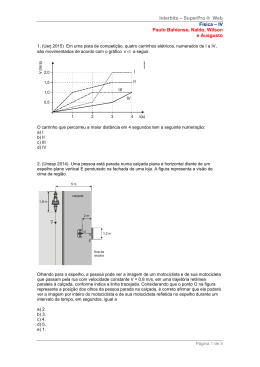
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
1. (Unifesp 2015) O pingente de um colar é constituído por duas peças, A e B, feitas de
materiais homogêneos e transparentes, de índices de refração absolutos nA  1,6  3 e
nB  1,6. A peça A tem o formato de um cone reto e a peça B, de uma semiesfera.
Um raio de luz monocromático R propaga-se pelo ar e incide, paralelamente ao eixo do cone,
no ponto P da superfície cônica, passando a se propagar pelo material da peça A. Atinge o
ponto C, no centro da base do cone, onde sofre nova refração, passando a propagar-se pelo
material da peça B, emergindo do pingente no ponto Q da superfície esférica. Desde a entrada
até a sua saída do pingente, esse raio propaga-se em um mesmo plano que contém o vértice
da superfície cônica. A figura 1 representa o pingente pendurado verticalmente e em repouso e
a figura 2, a intersecção do plano que contém o raio R com o pingente. As linhas tracejadas,
indicadas na figura 2, são paralelas entre si e α  30.
a) Calcule o valor do ângulo β indicado na figura 2, em graus.
b) Considere que a peça B possa ser substituída por outra peça B', com o mesmo formato e
com as mesmas dimensões, mas de maneira que o raio de luz vertical R sempre emerja do
pingente pela superfície esférica.
Qual o menor índice de refração do material de B' para que o raio R não emerja pela
superfície cônica do pingente?
Página 1 de 9
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
2. (Ufrgs 2015) Na figura abaixo, um raio luminoso i, propagando-se no ar, incide radialmente
sobe placa semicircular de vidro.
Assinale a alternativa que melhor representa a trajetória dos raios r1 e r2 refratados,
respectivamente, no vidro e no ar.
a)
b)
c)
d)
e)
Página 2 de 9
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
3. (Uel 2015) Analise o gráfico a seguir, que representa uma transformação cíclica ABCDA de
1mol de gás ideal.
a) Calcule o trabalho realizado pelo gás durante o ciclo ABCDA.
b) Calcule o maior e o menor valor da temperatura absoluta do gás no ciclo (considere
J
R8
). Justifique sua resposta apresentando todos os cálculos realizados.
K mol
Página 3 de 9
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
4. (Pucpr 2015) O físico e engenheiro francês Nicolas Léonard Sadi Carnot (1796-1832), em
seu trabalho Reflexões sobre a potência motriz do fogo, concluiu que as máquinas térmicas
ideais podem atingir um rendimento máximo por meio de uma sequência específica de
transformações gasosas que resultam num ciclo – denominado de ciclo de Carnot, conforme
ilustra a figura a seguir.
A partir das informações do ciclo de Carnot sobre uma massa de gás, conforme mostrado no
gráfico p  V, analise as alternativas a seguir.
I. Ao iniciar o ciclo (expansão isotérmica 1  2), a variação de energia interna do gás é igual a
QQ e o trabalho é positivo (W  0).
II. Na segunda etapa do ciclo (expansão adiabática 2  3) não há troca de calor, embora o
gás sofra um resfriamento, pois ΔU  W.
III. Na compressão adiabática 4  1, última etapa do ciclo, o trabalho realizado sobre o gás
corresponde à variação de energia interna dessa etapa e há um aquecimento, ou seja,
ΔU  W.
IV. O trabalho útil realizado pela máquina térmica no ciclo de Carnot é igual à área A ou, de
outro modo, dado por : τ  QQ  QF .
V. O rendimento da máquina térmica ideal pode atingir até 100 %, pois o calor QF pode ser
nulo – o que não contraria a segunda lei da termodinâmica.
Estão CORRETAS apenas as alternativas:
a) I, II e IV.
b) I, II e III.
c) II, III e IV.
d) II, III e V.
e) III, IV e V.
Página 4 de 9
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
5. (Unesp 2015) A figura representa, de forma simplificada, parte de um sistema de
engrenagens que tem a função de fazer girar duas hélices, H1 e H2 . Um eixo ligado a um
motor gira com velocidade angular constante e nele estão presas duas engrenagens, A e B.
Esse eixo pode se movimentar horizontalmente assumindo a posição 1 ou 2. Na posição 1, a
engrenagem B acopla-se à engrenagem C e, na posição 2, a engrenagem A acopla-se à
engrenagem D. Com as engrenagens B e C acopladas, a hélice H1 gira com velocidade
angular constante ω1 e, com as engrenagens A e D acopladas, a hélice H2 gira com
velocidade angular constante ω2 .
Considere rA , rB , rC , e rD , os raios das engrenagens A, B, C e D, respectivamente.
ω
Sabendo que rB  2  rA e que rC  rD , é correto afirmar que a relação 1 é igual a
ω2
a)
b)
c)
d)
e)
1,0.
0,2.
0,5.
2,0.
2,2.
Página 5 de 9
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
Gabarito:
Resposta da questão 1:
A figura ilustra duas trajetórias para o raio incidente, uma sofrendo emersão pelo ponto Q e, a
outra, pelo ponto S.
a) Aplicando a lei de Snell na interface cone-semiesfera:
3
 1
nA sen α  nB sen β  1,6 3    1,6 sen β  sen β 

2
2
β  60.
b) Para que a emersão seja rasante (pelo ponto S), o ângulo de refração deve ser igual a 90°.
Nesse caso, o angulo α torna-se o ângulo limite.
Aplicando novamente a lei de Snell:
 1
nA sen α  nB' sen 90  1,6 3    nB'  nB'  0,8 3 .
 2
Resposta da questão 2:
[A]
Ao incidir radialmente sobre uma superfície circular o raio não sofre desvio,
independentemente do sentido de propagação. Ao sair para o ar, o raio está passando do meio
mais refringente para o menor refringente, afastando-se da normal.
Página 6 de 9
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
Resposta da questão 3:
a) O trabalho do ciclo ABCDA representado na figura corresponde à área da figura,
considerando o sentido horário teremos um trabalho positivo. Os segmentos AB e CD em
que temos uma transformação isocórica (volume constante) terão trabalho nulo. No
seguimento BC teremos uma expansão volumétrica isobárica conduzindo a um trabalho
positivo (gás realizando trabalho sobre o meio externo) e no seguimento DA teremos o gás
recebendo trabalho do meio externo, ou seja, um trabalho negativo referente a uma
contração de volume à pressão constante.
A expressão do trabalho isobárico fica
τ  p  ΔV
Onde
τ  trabalho realizado (  ) ou recebido pelo gás ( ) em joules (J)
p  pressão do gás em Pascal (Pa  N m2 )
ΔV  variação de volume do gás (m3 )
τBC  15Pa  (6  2)m3  60J
e
τDA  5Pa  (2  6)m3  20J
O trabalho do ciclo é
τciclo  60  20  40J
Ou ainda pela área do retângulo
τciclo  (15  5)Pa  (6  2)m3  40J
b) Para calcularmos a maior e a menor temperatura do sistema devemos lembrar os gráficos
de isotermas, através da Lei de Boyle-Mariotti
Observando o gráfico dado notamos que os pontos de maior e menor temperaturas
absolutas são respectivamente C e A.
Para calcularmos estes valores de temperatura, lançamos mão da equação de estados dos
Gases Ideais
pV  nRT
Onde
p  pressão do gás em Pascal (Pa  N m2 )
Página 7 de 9
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
V  volume do gás (m3 )
n  número de mols do gás (mol)
R  constante universal dos gases ideais (fornecido no problema)
T  temperatura absoluta (K)
Isolando T e calculando as temperaturas para os pontos C e A, temos:
A maior temperatura
TC 
15Pa  6m3
 11,25K
J
1mol  8
molK
E a menor temperatura
TA 
5Pa  2m3
 1,25K
J
1mol  8
molK
Resposta da questão 4:
[C]
Analisando as afirmativas, temos:
[I] (Falsa) Em um processo isotérmico, a energia interna não varia, e, portanto sua variação é
nula ΔU  0;
[II] (Verdadeira) Não há troca de calor em um processo adiabático e como temos uma
expansão o trabalho que o gás realiza se dá à custa da energia interna causando um
resfriamento do sistema. ΔU  W;
[III] (Verdadeira) Neste caso temos a situação inversa da afirmativa [II], uma compressão
adiabática em que o calor é zero, logo haverá um aquecimento do gás graças ao trabalho
exercido sobre o gás. ΔU   W;
[IV] (Verdadeira) O trabalho útil do ciclo τ corresponde à área sob as curvas A ou ainda pela
diferença de calor entre a fonte quente e a fonte fria: τ  QQ  QF ;
[V] (Falsa) A Segunda Lei da Termodinâmica diz que é impossível construir uma máquina que
obedeça ao ciclo de Carnot com um rendimento de 100%, visto que é impossível converter
o calor de forma integral em trabalho.
Sendo assim, a alternativa correta é [C].
Página 8 de 9
Interbits – SuperPro ® Web
Física – IX
Paulo Bahiense, Naldo, Wilson
e Ausgusto
Resposta da questão 5:
[D]
Na posição 1:
 rB  2 r A .

 ω ω 
A
 B

 v C  vB 

 ωC  ω1 

vB
vB
 ωA 
 ωA  vB  2 ω A r A .
rB
2 rA
ωC rC  2 ωA rA .
ω1rC  2 ωA rA . (I)
Na posição 2:
 vD  v A  ω D rD  ωA rA .

 ω2  ωD .
 r r .
 C D
 ω2 rC  ωA rA . (II)
Dividindo membro a membro (I) por (II):
ω1 rC
2 ωA rA
ω1


 2.
ω2 rC
ωA rA
ω2
Página 9 de 9