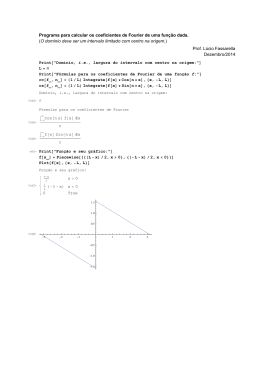
AS SÉRIES DE FOURIER
O que é uma série de Fourier.
Todo aluno de segundo grau
conhece as funções
trigonométricas, seno, cosseno,
tangente etc. A figura ao lado
mostra o familiar gráfico da função
sen(x), onde x é um ângulo
medido em radianos.
Essa função é PERIÓDICA, isto é,
sua forma se repete a cada
PERÍODO. No caso dessa figura,
a função seno se repete a cada
período de 2 . O valor máximo da
função, chamado de AMPLITUDE,
é 1.
A função cosseno também é periódica,
com o mesmo período e amplitude que o
seno, mas é deslocada de /2 em
relação ao seno.
Isso é fácil de constatar examinando os
gráficos. Tecnicamente, diz-se que as
funções seno e cosseno diferem na
FASE e a diferença de fase entre elas é
de /2.
Na figura ao lado, vemos a soma
(curva em vermelho) das funções
sen(x) e cos(x). Essa curva é
obtida traçando-se, em cada
ponto x, a soma dos valores de
sen(x) e cos(x) nesse ponto. Por
exemplo, o ponto da curva na
região x=5,5 é zero pois o valor de
sen(x) é igual e de sinal oposto ao
valor de cos(x) nesse ponto.
Verifique a situação para outros
pontos da curva para treinar pois
as séries de Fourier são
composições de muitas curvas
tipo seno e cosseno, como
veremos.
Uma função periódica pode ser bem mais
complicada que uma senóide. Veja o
exemplo da função f(x) mostrada na figura
ao lado. Essa curva também é periódica
mas, não é apenas um seno ou um
cosseno. Como achar uma função
matemática que descreva uma curva
como essa?
Foi isso que Fourier descobriu, no início do século 19. Segundo ele, qualquer
função periódica, por mais complicada que seja, pode ser representada
como a soma de várias funçoes seno e cosseno com amplitudes, fases e
períodos escolhidos convenientemente.
Existem alguns requisitos para que essa afirmação seja totalmente verdadeira.
Mas, eles são tão poucos e especializados que podemos ignorá-los nesse
relato simplificado.
470"> A figura ao lado mostra a mesma curva da figura acima juntamente com duas
funções seno e duas funções cosseno. A curva original é a soma dessas 4
funções, como você pode verificar com alguma paciência. Note que as amplitudes
e períodos das ondas componentes são diferentes entre si.
Matematicamente, a decomposição da função f(x) na curva acima é a
seguinte:
Em resumo, qualquer função f(x) pode, segundo Fourier, ser escrita na forma
da soma de uma série de funçoes seno e cosseno da seguinte forma geral:
Os pontinhos nessa equação indicam que os termos tipo seno e cosseno
podem se extender indefinidamente, se necessário, para melhor representação
da função original f(x).
Resta achar uma forma de calcular os coeficientes
etc, de
cada termo da série. Esses coeficientes, como vemos, são as amplitudes de
cada onda componente do desenvolvimento em série.
Pois foi isso que Fourier conseguiu fazer: achou uma forma simples e elegante
de calcular esses coeficientes, coisa que escapara de gigantes como Euler e
Bernouilli.
Veremos como isso é feito, mais adiante. Antes, porém, precisamos aprender
a calcular MÉDIAS de funções periódicas.