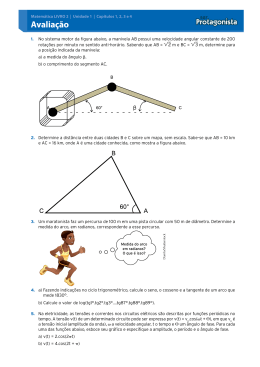
INFLUÊNCIA DA ATRAÇÃO LUNI-SOLAR SOBRE MEDIDAS GRAVIMÉTRICAS
A força da gravidade, já sabemos, é a resultante da força de atração gravitacional e da força
centrífuga produzida pela rotação da Terra. A ação gravitacional da Lua e do Sol introduz
variação na força de gravidade e conseqüentemente na aceleração medida sobre a superfície
terrestre.
Chama-se força de maré, em um ponto 𝑃, a diferença da atração exercida pela Lua e pelo Sol
sobre a unidade de massa colocada nesse ponto e no centro da Terra.
Seja 𝑀 a massa de um corpo celeste perturbador (Figura 1).
Figura 1 Força de maré
Nestas condições, a força de maré (em módulo) é expressa por
𝐹=
𝐺𝑀
𝑙2
−
𝐺𝑀
𝑟2
[1]
As componentes horizontal e vertical da força de maré são
𝐹ℎ = 𝐺𝑀
sin 𝑧 ′
𝑙2
−
cos 𝑧
𝑟2
[2]
𝐹𝑣 = 𝐺𝑀
cos 𝑧 ′
𝑙2
−
cos 𝑧
𝑟2
[3]
Eliminando, através de transformações que omitimos, a distância linear (𝑙) e a distância zenital
topocêntrica (𝑧′) do astro perturbador, vem
𝐹ℎ =
3𝐺𝑀𝑎 sin 2𝑧
2𝑟 3
𝐹𝑣 =
𝐺𝑀𝑎
𝑟3
=
3𝐺𝑀
2𝑎 2
𝑎3
sin 2𝑧
𝑟3
3 cos2 𝑧 − 1 =
𝐺𝑀
𝑎2
𝑎3
𝑟3
3 cos2 𝑧 − 1
mas 𝑎/𝑟 = 𝑝 é a paralaxe horizontal do astro perturbador. Logo
𝐹ℎ =
3𝐺𝑀𝑝 3 sin 2𝑧
2𝑎 2
[4]
𝐹𝑣 =
𝐺𝑀𝑝 3
𝑎2
[5]
3 cos2 𝑧 − 1
6.1 CASOS PARTICULARES
Os gravímetros nos proporcionam o módulo de 𝑔, isto é, 𝑔. Interessa-nos, portanto, a
componente vertical da força de maré, dada por [5].
A componente vertical será nula se (expressão [5])
3 cos2 𝑧 = 1
ou seja, quando
𝑧 = 54∘ 44′
e
𝑧 = 126∘ 16′
Para 𝑧 < 54∘ 44′, a componente vertical da atração exercida pelo astro perturbador em 𝑃 é
maior que a componente da atração exercida em 𝑂. O vetor diferença (componente vertical da
força de maré) é orientado para o zênite, opondo-se a 𝑔 e, portanto diminuindo o valor de 𝑔.
Logo exige uma correção positiva.
Para 𝑧 > 125∘ 16′ o astro se encontra abaixo do horizonte e a componente vertical da atração
em 𝑃 é menor que a componente vertical em 𝑂 (ambas com o mesmo sentido de 𝑔)
resultando o vetor diferença ainda orientado para o zênite de 𝑃, diminuindo o valor de 𝑔 e
exigindo uma correção positiva.
A correção é máxima quando o astro culmina superior ou inferiormente.
Para valores da distância zenital compreendidas entre 54∘ 44′ e 125∘ 16′ a correção é negativa,
o valor mínimo ocorrendo quando o astro se encontra no horizonte (𝑧 = 90∘).
3 cos 2 𝑧 − 1
0
+2,00
∘
40
+0,76
54∘ 44′
0,00
60∘
−0,25
90∘
−1,00
120∘
−0,25
125∘ 16′
0,00
∘
140
+0,76
180∘
+2,00
𝑧
∘
Tabela 1
A expressão [5] pressupõe uma Terra perfeitamente rígida o que, na realidade, não se verifica.
A Geofísica dispõe de métodos e equipamentos que permitem constatar que os efeitos reais
da força de maré são superiores aos proporcionados teoricamente por [5], em virtude da
elasticidade que devemos atribuir ao nosso planeta.
Para considerar esta componente, usualmente é incluído o fator 1,2 na fórmula [5], fazendo
ainda a aproximação
𝐺𝑀𝑇
𝑎2
=𝑔
Ou simplesmente
𝐺
𝑎2
= 𝑔 (massa terrestre unitária)
Onde 𝑔 representa o valor médio. Com isso resulta
𝐶𝑔 = 1,2𝑔𝑝3 𝑀𝑇 3 cos2 𝑧 − 1
[1.1]
Onde 𝑀𝑇 é a relação entre a massa do astro perturbador e a massa da Terra.
Com os valores numéricos da Tabela 2
𝑀𝑇
𝑝𝑚𝑎𝑥
𝑝𝑚𝑎𝑥
Lua
Sol
1: 80 = 0,0125
333 432
61,6′
8,9′′
1,7918 × 10−2 rad 4,3148 × 10−5 rad
Tabela 2 Proporção de massas e paralaxe máxima
e considerando a máxima aproximação do astro resulta
𝐶𝑔𝐿𝑢𝑎 = 0,085 (3 cos 2 𝑧 − 1)
[1.2]
𝐶𝑔 𝑆𝑜𝑙 = 0,032 (3 cos2 𝑧 − 1)
[1.3]
Nas condições anteriores, se o astro atinge o zênite ou o nadir
max 𝐶𝑔𝐿𝑢𝑎 = 0,170 mGal
max 𝐶𝑔 𝑆𝑜𝑙 = 0,064 mGal
Resultando para o máximo efeito combinado possível
max 𝐶𝑔 = 0,234 mGal
6.2 CORREÇÃO DA ATRAÇÃO LUNI-SOLAR NAS MEDIDAS GRAVIMÉTRICAS
Digamos que uma estação gravimétrica tenha sido medida às 𝐻𝐿 horas legais. Convertendo 𝐻𝐿
em hora civil 𝐻𝐶 e sideral 𝑆, calcula-se o ângulo horário do astro perturbador
𝐻 = 𝑆−𝛼
[2.1]
Sendo 𝛼 a ascensão reta do mesmo.
Considerando que algumas efemérides (Almanaque Náutico da DHN, p.ex.) proporcionam o
ângulo horário da Lua e do Sol referidos ao meridiano de Greenwich (𝐻𝐺 ) para as horas cheias
do tempo universal e para todos os dias do ano, obtém-se mais facilmente
𝐻 = 𝐻𝐺 − 𝜆
[2.2]
Sendo 𝜆 a longitude da estação.
Podemos, então, calcular a distância zenital do astro para o instante da observação
gravimétrica.
cos 𝑧 = sin 𝜑 sin 𝛿 + cos 𝜑 cos 𝛿 cos 𝐻
[2.3]
A expressão [1.1] aplicada aos dois astros (Lua e Sol) proporciona a correção 𝐶𝑔 .
Existem tabelas que facilitam os cálculos:
- As de Damrel, publicadas pelos fabricantes do gravímetro Worden, por exemplo, exigem uma
efeméride como a mencionada;
-As publicadas pela European Association of Exploration Geophysicists, dispensam as
efemérides.
Há também gráficos que propiciam a correção relativa ao efeito da componente vertical da
maré nas medidas gravimétricas em determinadas regiões como, por exemplo, os que vêm
sendo publicados pelo Curso de Pós-graduação em Ciências Geodésicas da UFPR.