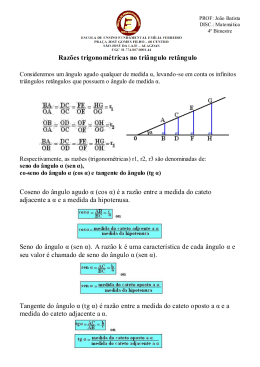
ATIVIDADE INICIAL 1
Título da Atividade: Comparando triângulos
a) Quantos triângulos você enxerga na figura? Escreva os seus nomes (por
exemplo: ∆ ABC) ∆ ABC, ∆ BEF, ∆ BDG
b) Todos eles possuem uma característica em comum. Qual é esta característica?
Todos são triângulos retângulos, possuem um ângulo reto. O aluno também
pode dizer que possuem lados paralelos, que são três triângulos semelhantes
e que possuem os três ângulos homólogos congruentes.
c) Meça os lados indicados abaixo com o auxílio de uma régua e preencha a
tabela. (você pode utilizar uma calculadora)
Triângulo 1
= Lado
b = Lado
c = Lado
Triângulo 2
= Lado
b = Lado
c = Lado
Triângulo 3
= Lado
b = Lado
c = Lado
Medidas em cm
3 cm
5,2 cm
6 cm
0,57
0,86
0,5
0,58
0,86
0,5
0,58
0,86
0,5
Medidas em cm
4 cm
6,9 cm
8 cm
Medidas em cm
5 cm
8,6 cm
10 cm
d) Observando os resultados encontrados, o que podemos concluir?
Os resultados das razões praticamente se mantiveram constantes. Isso se dá devido à
semelhança dos triângulos que gera a constante de proporcionalidade. Os valores só
não foram totalmente iguais devido à presença dos lados denominados “b” que
possuem, na realidade, medidas irracionais (impossíveis de se medir com exatidão
através de uma régua)
ATIVIDADE INICIAL 2
Título da Atividade: Um caminho para o curral
Caça ao tesouro
Antônio está participando de uma gincana em sua escola. Ele está disputando
uma prova de caça ao tesouro e precisa da sua ajuda. Ele precisa escolher por
qual caminho ele deve atravessar o milharal para encontrar o tesouro. Ele só
cumpre a tarefa se escolher o caminho que leva diretamente ao tesouro!
Se ele pudesse contornar o milharal, ele teria que andar 10 metros até a
esquina e depois mais 8,4 metros até o tesouro.

O primeiro caminho forma um ângulo
de 30° com o lado do muro (que mede
10 metros) que cerca o milharal.

O segundo caminho forma um ângulo
de 40° com o lado do muro (que
mede 10 metros) que cerca o
milharal.
1. Para cada caminho, use a tangente para calcular o comprimento do
cateto oposto ao ângulo que ele faz com o lado do muro que mede 10
metros.
Nos dois caminhos, o cateto adjacente coincide com o lado do muro que
mede 10 metros. Para determinar a medida do cateto oposto, vamos
multiplicar a medida do cateto adjacente pela tangente do ângulo:
catetooposto
Primeiro caminho
Segundo caminho
ângulo
30°
40°
catetoadjacente
tangente
0,58
0,84
tangentedoângulo
Cateto oposto
catetooposto
10 0,58
catetooposto
10 0,84
5,8metros
8,4metros
2. Use o exercício anterior para ajudar Antônio a escolher o caminho que
leva ao tesouro.
Para chegar diretamente ao tesouro, Antônio deve escolher o caminho
que termine a 8,4 metros da esquina. Os valores obtidos no exercício
anterior indicam que Antônio deve tomar o segundo caminho.
ATIVIDADE xxx
Título da Atividade: Engenharia da trigonometria (lei dos consenos)
Os alunos deverão utilizar a fórmula da lei dos cossenos para solucionar
facilmente o problema.
50
40
2 ∙ 50 ∙ 40 ∙ cos 60 1
2500 1600 4000 ∙ 2
4100 2000
2100
√2100 ≅ 45,8
ATIVIDADE xxx
Título da Atividade: Os ângulos e as torres
Problema
Para calcular a altura da torre em cada ano, vamos
proceder como no vídeo: vamos indicar por
o ângulo
de inclinação da torre, vamos identificar o comprimento
da torre com a hipotenusa do triângulo retângulo e a
altura com o cateto adjacente ao ângulo de inclinação da
torre. Sabemos que o comprimento da torre é de 58
metros. Portanto,
altura
comprimento
cos
Portanto,
altura
comprimento cos
Com auxílio dos dados do problema, calculamos:
Ano
1292
Ângulo de inclinação
1,5°
1817
4
1990
°
5,5°
cos
Altura da torre de Pisa
0,999657 58
0,997564 58
0,999657
57,9812 metros
0,997564
57,85871 metros
0,995396
0,995396
57,73298 metros
58
ATIVIDADE xxx
Título da Atividade: Batendo pênalti
Batendo pênalti
O cronômetro já marca 42 minutos do segundo tempo e o juiz marca pênalti
contra o Flamengo!
Você conhece as regras para a cobrança de pênalti?
A bola deve ser colocada a 11 metros do ponto médio da linha do gol.
O gol tem 7,32 metros de largura e 2,44 metros de altura.
A cobrança usual do pênalti é feita por meio de um tiro direto, e uma das
consequências é que a trajetória da bola, em função da distância e da
velocidade, pode ser considerada, em grande parte das experiências, uma
linha reta. Assim, faremos a visualização das vistas lateral e superior desses
chutes, pontilhando as trajetórias das bolas em direção ao gol.
Problemas:
1. Se olharmos a cobrança do pênalti lateralmente, podemos visualizar um
triângulo retângulo. Um de seus catetos corresponde a uma das traves
(altura do gol) e outro à distância dos 11 metros da marca do pênalti até
o gol (representada pela linha vermelha).
Use as razões trigonométricas no triângulo retângulo e a Tabela 1 para
obter um valor aproximado do ângulo máximo de saída da bola para que
o jogador marque gol. (Pense em um chute em que bola passe por baixo
e rente à trave superior. Essencialmente, você deve determinar o ângulo
entre a linha pontilhada que passa rente à trave e a linha vermelha).
A partir do esquema da vista lateral, podemos representar um
chute em que bola passe por baixo e rente à trave superior através de
um triângulo retângulo. Um de seus catetos corresponde a uma das
traves (altura do gol) e outro à distância dos 11 metros da marca do
pênalti até o gol (representada pela linha vermelha).
Vamos denotar por
o ângulo do chute: o ângulo formado entre a linha
pontilhada e a linha vermelha.
tg
catetooposto
catetoadjacente
2,44m
11m
0,22
Um consulta à Tabela 1 permite concluirmos que o ângulo de chute não
pode superar 13° .
2. Se olharmos de cima a cobrança do pênalti, podemos visualizar um
triângulo isósceles cuja base coincide com a largura do gol e cuja altura
coincide com a distância do gol à marca do pênalti. A medida da base é
7,32 metros e sua altura mede 11 metros.
Use as razões trigonométricas no triângulo retângulo e a Tabela 1 para
obter um valor aproximado do ângulo máximo de saída da bola para que
o jogador marque gol. (Pense em um chute rasteiro em que bola passe
em um dos cantos inferiores do gol. Essencialmente, você deve
determinar o ângulo entre a linha pontilhada e a linha laranja).
Para determinarmos o ângulo máximo de
saída da bola em um chute rasteiro, vamos
imaginar um chute para o canto inferior direito do
gol. Ele também pode ser representado por um
triângulo
retângulo.
Um
de
seus
catetos
corresponde à distância dos 11 metros da marca
do pênalti até o gol (representada pela linha
laranja) e o outro corresponde à metade da largura
do gol.
Vamos denotar por
o ângulo do chute: o ângulo formado entre a linha
pontilhada e a linha laranja.
tg
catetooposto
catetoadjacente
3,66m
11m
0,33
Um consulta à Tabela 1 permite concluirmos que o ângulo de chute não
pode superar 19° (à direita ou à esquerda).
Tabela 1
ATIVIDADE xxx
Título da Atividade: Cálculo de distâncias inacessíveis
1. Dois topógrafos estão na mesma margem de um rio, separados 36
metros um do outro. Um deles observa uma pedra que está na outra
margem, bem em frente ao seu companheiro. Com a ajuda de
um teodolito, o observador verifica que a linha perpendicular que une a
pedra ao colega forma um ângulo de 36º com a linha de mira do
teodolito à pedra. Qual é a largura do rio? (Dados: tg 36º = 0,727, sen
36º = 0,588 e cos 36º = 0,809).
Basta uma aplicação direta do cálculo da tangente de 36º.
0,727
tg36°
catetooposto
catetoadjacente
36m
36
≅ 49,52metros
0,727
2. Determine a altura da nuvem detectada pelo radar de acordo com a
figura acima. (Dados: sen 4º = 0,077, cos 4º= 0,998 e tg 4º=0,070).
Basta uma aplicação direta do cálculo da tangente de 4º.
0,07
tg4°
altura
catetooposto
catetoadjacente
80km
altura
80
≅ 5,6quilômetros
0,07
ATIVIDADE xxx
Título da Atividade: Calculando distâncias
Construindo uma ponte
Você foi orientado por seu chefe a efetuar as medições indicadas na figura. Ele
afirmou que conhecendo a medida de dois lados do triângulo e de dois
ângulos, com alguns cálculos, você seria capaz de determinar o comprimento
da ponte. As medidas dos lados foram feitas em metros.
1. Utilize a os dados da figura e os da tabela abaixo para determinar o
comprimento da ponte.
ângulo
33
115
Pela Lei dos Senos
sen
0,544639
0,906308
cos
0,838671
-0,422618
comprimentodaponte
sen115°
210m
sen33°
comprimentodaponte
210
0,906308
0,544639
comprimentodaponte
210
0,906308
0,544639
tg 0,649408
-2,144507
≅ 249,51metros
Encanamento
2. A água utilizada na casa de um sítio é captada e bombeada do rio para
uma
caixa-d’água
a
50
m
de
distância.
Sabemos
que
ângulo formado pelas direções (caixa d’água-casa) e (caixa d’água-b
omba) é de 45º e que o ângulo formado pelas direções (bomba-caixa
d’água) e (caixa d’água-casa) é de 60º. Se pretendermos bombear
água
do
mesmo
ponto
de
captação
diretamente
até
a
casa, quantos metros de encanamento são necessários? (Dados: tg
45º = 1, sen 45º = 0,707107 e cos 45º = 0,707107; tg 60º = 1,732051,
sen 60º = 0,866025 e cos 60º = 0,5).
Pela Lei dos Senos
encanamento
sen60°
encanamento
0,866025
encanamento
50
50m
sen45°
50
0,707107
0,866025
≅ 61,24metros
0,707107