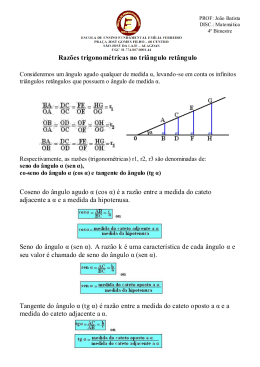
“Três” “ângulo” “medida”
“A medida dos três ângulos”
A relação entre os
lados e os ângulos dos
triângulos
Astronomia
Cartografia
Medicina
Fenómenos
oscilatórios
[PQR] é um Triângulo Rectângulo
porque um dos seus ângulos é recto.
Quanto aos lados, um Triângulo
rectângulo é constituído por:
. Uma hipotenusa
P
( O lado oposto ao ângulo recto, neste caso [PR] )
Cateto
. Dois Catetos
(Os lados que formam o ângulo recto, neste caso
[RQ], e [PQ]
R
Cateto
Q
[PQR] é um Triângulo Rectângulo
porque um dos seus ângulos é recto.
P
Sabemos que um triângulo deste tipo
Verifica o Teorema de Pitágoras, ou
seja :
2
2
PR = RQ +
PQ
2
Cateto
R
Cateto
Q
“O quadrado da hipotenusa é igual à
soma dos quadrados dos catetos “
Exemplo 1:
Determinemos o valo de x aplicando o
Teorema de Pitágoras:
x
2
2
3 = 1 + x2
2
1
9 = 1 + x
3
2
x =8
x =
x =
8
8 , porque se trata de um comprimento
Teorema de Pitágoras
P
β
Relaciona apenas o comprimento
entre os lados do triângulo
Trigonometria
α
R
Q
Permite relacionar o comprimento
dos lados com a amplitude dos
ângulos do triângulo
Em relação ao ângulo α:
P
β
. [RQ] é o cateto adjacente
Em relação ao ângulo β:
α
R
. [PQ] é o cateto oposto
Cateto oposto a β
Q
. [RQ] é o cateto oposto
. [PQ] é o cateto adjacente
Consideremos a, b e c as medidas
dos lados do triângulo[PQR].
Chamamos seno do ângulo α, e
representamos por sen α, à razão:
Comprimento do cateto oposto a α
β
sen α =
c
Comprimento da hipotenusa
a
α
Denominamos co-seno do ângulo α,
e representamos por cos α , à razão:
b
sen α =
a
c
b
cos α =
c
cos α =
Comprimento do cateto adjacente a α
Comprimento da hipotenusa
Consideremos a, b e c as medidas
dos lados do triângulo[PQR].
Chamamos tangente do ângulo α, e
representamos por tan α, à razão:
Comprimento do cateto oposto a α
β
tan α =
c
Comprimento do cateto adjacente
a
α
Às razões seno, co-seno e tangente
b
Chamamos razões trigonométricas
tan α =
a
b
Exemplo 2:
5
sen α =
β
4
α
3
4
5
3
cos α =
5
4
tan α =
3
Cada uma destas razões isoladamente
identifica o ângulo agudo α.
5
α = 53,13º
β
4
Devemos utilizar a razão que melhor
se adapta aos nossos dados quando
pretendemos conhecer a amplitude do
ângulo
Neste caso,
sen α = 4/5
usando uma calculadora :
sen-1 ( 4/5) = 53,13º( 2 c.d.)
Exemplo 3:
Pretendemos determinar a altura h de um
edifício cujo topo define com o solo, um ângulo
de 60º a 30 metros da sua base:
tan 60º =
h
h
30
h = 30 × sen 60º
60º
30 m
(Recorrendo à calculadora )
h = 51,96 m ( 2 c.d.)
A altura do edifício é aproximadamente de 51, 96 metros
Repare-se que
b
a
sen 30º =
30º
a
b
d
=
c
d
= e
Ou seja:
c
30º
1
e
30º
O valor do seno de um ângulo
agudo
é
independente
das
dimensões do triângulo rectângulo
do qual faz parte. Por isso é
cómodo trabalhar com um triângulo
de hipotenusa igual a 1
ISTO É SÓ O COMEÇO!!
BOA TRIGONOMETRIA!....