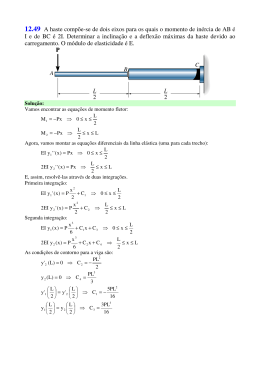
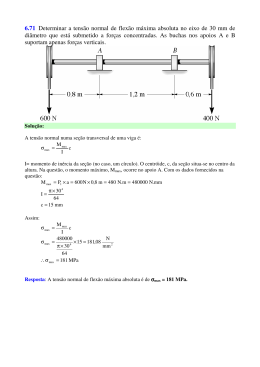
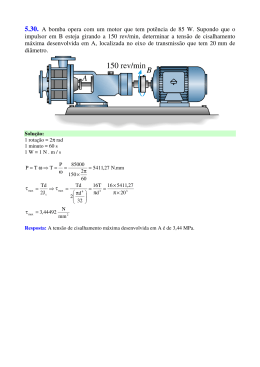
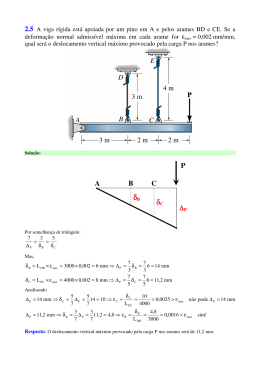
Algoritmo de Eliminação Gaussiana com Pivotamento Parcial
Entrada:
A[i,j] matriz mxm associada a um sistema de equações lineares
b[i]
vetor coluna de m posições associado a um sistema de equações lineares
Saída:
A[i,j] modificada pelo processo de eliminação;
b[i]
modificado pelo processo de eliminação.
Observações:
i)
ii)
iii)
Os valores da matriz triangular inferior não são anulados pois tal operação é
computacionalmente desnecessária na aplicação do algoritmo de
retrosubstituição;
argmax() é uma função que devolve o índice da linha que contém o maior
valor em módulo da coluna em processo de eliminação;
troca_linhas() troca a linha que contém o pivot com a linha que contém o
maior valor em módulo da coluna que está sendo eliminada.
para k = 1 até n:
/* Determinação da linha onde o pivot da coluna k é máximo:
i_max := argmax (i = k ... n, abs(A[i, k]))
se A[i_max, k] = 0 então "A matriz é singular"; Pare.
troca_linhas(k, i_max)
/* Eliminação dos elementos da coluna k abaixo da diagonal
para i = k + 1 até n:
/* Fator de multiplicação necessário à eliminação em cada linha da coluna que está em processo
/* de eliminação
m = A[i, k] / A[k, k]
para j = k + 1 até n:
A[i, j] := A[i, j] - A[k, j] * m