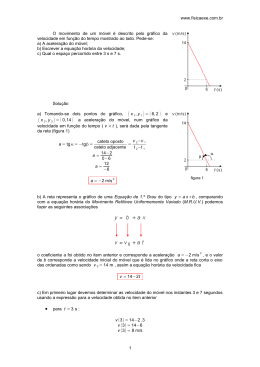
III) M.U.V. = Movimento Uniformemente Variado
am 
CINEMÁTICA
I) Velocidade Média
Vm 
S
t
Vm = Velocidade escalar
média (m/s)
S = Variação do espaço (m)
S  So
Vm 
t  to
km/h
18
36
54
72
90
108
÷ 3,6
t = Variação do tempo (s)
m/s
5
10
15
20
25
30
V  Vo
t  to
Função horária do espaço
a.t 2
S  S o  Vo .t 
2
Dica: Quando o móvel
passa pela origem, adote
S = 0 para encontrar este
instante (t).
Função horária da
velocidade
V  Vo  a.t
Dica: Quando o móvel
muda de sentido, adote
V = 0 para encontrar este
instante (t).
Equação de Torricelli
2
V 2  Vo  2.a.S
A velocidade varia
sempre na mesma
proporção segundo
uma progressão
aritmética com uma
aceleração constante
e diferente de zero.
am = Aceleração
escalar média (m/s2)
V = Velocidade final
(m/s)
Vo = Velocidade
inicial (m/s)
S = Posição final (m)
So = Posição inicial
(m)
t = tempo final (s)
to = tempo inicial (s)
Velocidade média
II) M.U. = Movimento Uniforme
Vm 
S  So
t  to
Função horária do
espaço
S  S o  V .t
É aquele cuja a
velocidade escalar é
constante e diferente
de zero.
Vm 
S = variação do
espaço (m)
t = variação do
tempo (s)
S  So
t  to
S = Posição final (m)
So = Posição inicial (m)
a  0 (aceleração nula )
Importante: Só pode
calcular Vm se no exercício
vier pedindo claramente
“Calcule a Velocidade
Média”. Caso contrário,
elas não deverão ser usadas.
Quando se tratar de M.U.V.
pode usar:
t = Tempo final (s)
to = Tempo inicial (s)
Vm 
V  Vo
2
www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692
Pág. 1
IV) Lançamento Vertical e Queda Livre
Em ambos os casos adote:
1) g = aceleração da gravidade.
Para a Terra usar g = – 10m/s2
Para a Lua usar g = – 1,6 m/s2.
2) No chão (solo) a altura é zero, ou seja:
So = 0  altura inicial ou de saída é o solo.
S = 0  altura final ou de chegada é o solo.
Convenção de sinais:
Objeto subindo  V +
Objeto descendo  V –
Lançamento Vertical:
Queda Livre:
Função horária do
espaço
g.t 2
S  S o  Vo .t 
2
DICA: para achar o
tempo total até a
chegada no solo, adote
S = 0.
Função horária do
espaço
g.t 2
S  S o  Vo .t 
2
DICAS: Se o objeto é
abandonado de uma
certa altura Vo = 0.
Para saber o tempo de
chegada ao solo S = 0.
Função horária da
velocidade
V  Vo  g.t
DICA: para achar o
tempo de subida (para
atingir a altura máxima)
adote V = 0.
Função horária da
velocidade
V  Vo  g.t
Equação de Torricelli
2
V 2  Vo  2.g.S
DICA: para achar a
altura máxima adote
V = 0 e ache o valor de
S. Caso ele não tenha
saído do solo:
HMAX = S + So
Equação de Torricelli
2
V 2  Vo  2.g.S
www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692
Pág. 2
V) Gráficos de Movimento e Classificação
M.U. (Exemplos)
M.U. (Exemplos)
Obs.: Os três gráficos representam o mesmo
movimento.
Obs.: Os três gráficos representam o mesmo
movimento.
V (+)
V (–)
Gráfico: S x t
Gráfico: V x t
Gráfico: S x t
Gráfico: V x t
S = So + V.t
(reta crescente)
V = constante
(reta constante)
S = So + V.t
(reta decrescente)
V = constante
(reta constante)
So = -20 m (posição
inicial)
t = 2s (instante em que o
móvel passa pela
origem, S = 0)
V = + 10 m/s
(movimento
progressivo, V +, e
velocidade constante)
S = área do gráfico
Gráfico: a x t
a = 0 (zero) pois a
velocidade é constante
S = área do gráfico
So = 55 m (posição
inicial)
t = 55s (instante em que
o móvel passa pela
origem, S = 0)
Gráfico: a x t
a = 0 (zero) pois a
velocidade é constante
V = - 1 m/s
(movimento retrógrado,
V -, e velocidade
constante)
www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692
Pág. 3
M.U.V. (Exemplos)
M.U.V. (Exemplos)
Obs.: Os três gráficos representam o mesmo
movimento.
Obs.: Os três gráficos representam o mesmo
movimento.
a (+)
a (–)
Gráfico: S x t
Gráfico: V x t
Gráfico: S x t
Gráfico: V x t
S = So + Vo.t + a.t2/2
V = Vo + a.t
S = So + Vo.t + a.t2/2
V = Vo + a.t
So = 7,5 m (posição
inicial)
S = área do gráfico
t = 1s e 3s (instantes em
que o móvel passa pela
origem, S = 0)
Gráfico: a x t
t = 2s (a velocidade é
zero)
a = + 5 m/s2 (aceleração
constante)
De 0 a 2 s o movimento é V = área do gráfico
retrógrado, pois a
velocidade é negativa, e
retardado pois a
velocidade está
diminuindo além de V e a
terem os sinais opostos, V
–ea+
Após 2s o movimento é
progressivo, pois a
velocidade é positiva, e
acelerado, pois a
velocidade está
aumentando além de V e
a terem os mesmos sinais,
V+ea+
So = -10 m (posição
inicial)
t = 2s e 5s (instantes em
que o móvel passa pela
origem, S = 0)
S = área do gráfico
Gráfico: a x t
t = 3,5s (a velocidade é
zero)
a = – 1 m/s2 (aceleração
constante)
De 0 a 3,5s o movimento
é progressivo, pois a
velocidade é positiva, e
retardado pois a
velocidade está
diminuindo além de V e a
terem os sinais opostos, V
+ea–
V = área do gráfico
Após 3,5s o movimento é
retrógrado, pois a
velocidade é negativa, e
acelerado, pois a
velocidade está
aumentando além de V e
a terem os mesmos sinais,
V–ea–
www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692
Pág. 4