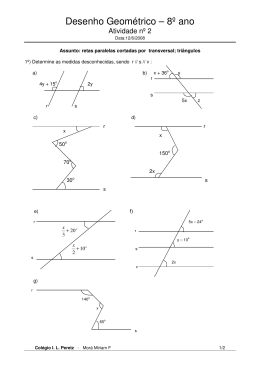
Valor do Trabalho:
2,0
ENSINO FUNDAMENTAL II
Nota:
Data: ____/____/2015
Professor
Professora:Cintya
Ribeiro
Disciplina: MATEMÁTICA
no:
Nome:
ANO
ANO:8º
___
3º
bimestre
TRABALHO
TRABALHODE
RECUPERAÇÃO DE MATEMÁTICA
ORIENTAÇÕES:
1- Leia todas as questões atentamente.
2- A interpretação das questões faz parte do seu trabalho.
3- Utilize caneta azul ou preta para as respostas que deverão ser em folha de papel
almaço. (OBS. Não é necessário copiar as questões, apenas indicá-las
indicá
colocando o
número e a letra da questão.)
01.
a)
b)
c)
d)
e)
olva os produtos notáveis abaixo:
Desenvolva
( x + 1 ) . ( x + 7) =
(x–8).(x–4)=
( 3x + 5y )3 =
( x + 3b )2 =
( 6a – 2c )2 =
02.
a)
b)
c)
d)
e)
Fatore as expressões algébricas
x2 – xy + 2x – 2y=
x2+xy–3x – 3y=
x2 –12x + 36 =
4k2 – 16m2 =
16b2+ 8by + y2 =
03.
Determine o valor numérico das expressões algébricas abaixo conforme os valores de x,
y e z indicados:
z=
para x = 1, y = 2 e z = 3
a) y2 –xy + xz+ yz
2
b) x + 2y – 2x + xy =
para x = 3 e y = 5
c) x2 – y2 =
para x = 8 e y = -3
d) x3 + 3x2y + 3xy2 + y3
para x = 7 e y = 1
e) 36 – 12x = x2
para x =
04.
A.
B.
C.
D.
E.
F.
05.
Determine o mmc e o mdc entre as expressões algébricas abaixo:
x3 – 1 e x – 1
x2 – 5x + 6 e x – 2
(x + 1) . (x + 2) e (x2 – 1)
2x + 10 e x2 – 25
x3 – 1 e 6x3 – 6
40x, 20x2 e 10x3
G.
H.
I.
J.
K.
6x2y, 3x2y3 e 10x3y2
x, x + 1, x + 2
4x2y, 9xy3
x2 – 9, x2 – 6x + 9
9x2 – 1, 3x – 1, 6x + 2
Em relação ao volume dos sólidos, efetue as operações indicadas.
A.
B.
C.
D.
V2
V1
V1
V1
+
+
+
+
V3
V2
V2
V3
= 61. V2 – V3 =
+ V3 =
– V3 =
=
06. Na figura abaixo as retas m e n são paralelas. Os ângulos de medidas x e 40º são:
a. (
) congruentes, pois são colaterais internos.
b. (
) congruentes, pois são correspondentes.
c. (
) congruentes, pois são alternos internos.
d. (
) suplementares, pois são colaterais internos.
e. (
) suplementares, pois são correspondentes.
07. Na figura abaixo as retas m e n são paralelas. A diferença
entre as medidas dos ângulos indicados por n e m é igual a:
a. (
) 5ºb. (
c. (
) 12ºd. (
e. (
) 18º
) 10º
) 15º
08. Se duas retas paralelas são cortadas por uma transversal, então a afirmativa falsa é:
a. (
) Os ângulos colaterais internos são congruentes.
b. (
) Os ângulos correspondentes são congruentes.
c. (
) Os ângulos alternos internos são congruentes.
d. (
) Os ângulos alternos externos são congruentes.
e. (
) Os ângulos opostos pelo vértice são congruentes.
09. Na figura abaixo as retas r e s são paralelas.
Qual a medida do ângulo a?
a. (
) 30ºb. (
) 40º
c. (
) 45ºd. (
) 50º
e. (
) 60º
10. Na figura abaixo há duas retas paralelas. Nestas condições, a
medida de θ é:
a. (
) 30°b. (
) 40°
c. (
) 45°d. (
) 50°
e. (
) 60°
11. Duas paralelas cortadas por uma transversal formam ângulos colaterais internos em que a
medida de um deles é a quarta parte da medida do outro. Quanto mede cada ângulo obtuso
formado pelas paralelas com a transversal?
a. (
) 95ºb. (
) 108ºc. (
) 120ºd. (
) 135ºe. (
) 144º
12. Duas retas paralelas cortadas por uma transversal, determinam dois ângulos colaterais
internos, em que a medida de um deles é o triplo da medida do outro. A diferença entre as
medidas dos ângulos obtuso e agudo é igual a:
a. (
) 45ºb. (
) 60ºc. (
) 75ºd. (
) 80ºe. (
) 90º
13. Uma reta transversal corta duas paralelas formando ângulos correspondentes cujas
medidas são expressas por (5x – 48º) e(3x + 12º). A medida de cada ângulo agudo formado é
igual a:
a. (
) 83º
b. (
) 78º
c. (
) 72º
d. (
) 65º
e. (
) 54º
14. A soma dos quatro ângulos agudos formados por duas retas paralelas cortadas por uma
o
reta transversal é igual a 80 . Nestas condições, podemos concluir que cada ângulo obtuso
mede:
a. (
) 150ºb. (
) 155ºc. (
) 160ºd. (
) 165ºe. (
) 170º
15. Na figura abaixo as duas retas são paralelas. Conclui-se que x+y é igual a:
a. (
) 180o
b. (
) 230o
c. (
) 250o
d. (
) 280o
e. (
) 300o