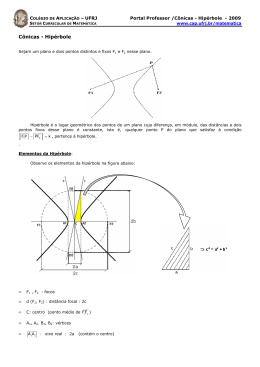
A Propriedade do Foco de uma Hipérbole
Conceito Principal
A hipérbole consiste de duas curvas abertas e disconexas chamadas de ramos, que são imagens
especulares uma da outra e se assemelham a arcos infinitos.
O ponto em que estes ramos estão mais juntos, e, portanto, mais próximos do centro são chamados de
vértices.
O segmento de reta entre os dois vértices é conhecido como o eixo principal ou transversal.
Além dos vértices na mesma linha que o eixo maior (que se encontra mais distante do centro), existem
dois pontos, E e F, que são os focos.
Uma hipérbole pode ser descrita como o locus de pontos para os quais os valores absolutos da
diferença entre as distâncias de qualquer ponto P a cada foco é uma constante.
Em especial, a diferença entre estas distâncias é sempre igual ao comprimento do eixo maior.
A equação geral para uma "abertura Leste-Oeste da hipérbole " é:
,
enquanto que a equação geral para uma "abertura Norte-Sul da hipérbole" é:
,onde
o centro, a é o comprimento do eixo semi-maior (a distância
de cada vértice para o centro), e também b é o comprimento do eixo semi-menor (a distância
perpendicular a partir de cada vértice de cada assíntota).
Derivação da equação geral da propriedade focal
Assíntotas
Clique para adicionar dois pontos para o gráfico a seguir para definir o seu focos, E e F.
Em seguida, escolha o botão de rádio "Pontos de Gráfico" e clique no gráfico para colocar os
pontos criando uma hipérbole.
Marque a caixa de seleção "Mostrar Hipérbole" para ver a curva real e sua equação, e marque a
caixa de seleção "Mostrar Assíntotas" para ver as assíntotas e suas equações.
Clique em "Limpar" para repor o gráfico.
Ajustar Focos
Colocar os Pontos
Distância do Foco E até último
ponto =
Distância do Foco F até o último
ponto =
Diferença entre as Distâncias =
Show Hyperbola
Equação da Hipérbole:
Show Asymptotes
Equações das Assíntotas:
Reiniciar