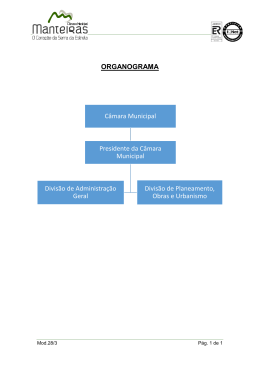
Imersão Olı́mpica
Introdução à Teoria dos Números
Eduardo Tengan (ICMC-USP)
20 a 23 de janeiro de 2009
Capı́tulo 1
Divisibilidade e Congruências
Neste capı́tulo, introduzimos dois conceitos fundamentais em Teoria dos Números que serão utilizados ao
longo de todo o livro: a relação de divisibilidade e a de congruência módulo um número inteiro.
1.1
Divisibilidade
Um dos conceitos primordiais em Teoria dos Números é o da divisibilidade.
Definição 1. Dados inteiros dois inteiros d e a, dizemos que
d divide a
ou
d é um divisor de a
ou
a é um múltiplo de d
e escrevemos
d|a
se existe um inteiro q tal que a = dq. Em outras palavras, se d 6= 0, dizer que d | a é o mesmo que dizer que
a fração ad é um inteiro.
Se d não divide a (equivalentemente, d não é um divisor de a ou a não é um múltiplo de d), escrevemos
d ∤ a.
Exemplo 2. Temos que
• 6 | 12 mas 12 ∤ 6;
• d | 4 se, e somente se, d ∈ {±1, ±2, ±4};
• Um número a é par se, e somente se, 2 | a;
• d | 0, d | d e d | −d para todo inteiro d;
• 0 | 0, já que existe um inteiro q tal que 0 = 0 · q (qualquer inteiro q serve), muito embora a fração
não esteja definida.
As duas propriedades mais importantes da divisibilidade são as seguintes:
Teorema 3.
1. (“d menor”) Se a 6= 0 então
d | a =⇒ |d| ≤ |a|
1
0
0
2. (“d divide”) Dados dois múltiplos a e b de d, qualquer combinação Z-linear de a e b (i.e., uma expressão
da forma ax + by com x, y ∈ Z) é um múltiplo de d. Em sı́mbolos:
(
d|a
=⇒ d | (ax + by)
d|b
Demonstração. Se d | a temos que existe um inteiro q tal que a = dq. Por outro lado, como a 6= 0, temos
também que q 6= 0, ou seja, |q| ≥ 1. Logo
a = dq =⇒ |a| = |d| · |q| ≥ |d| · 1 = |d|
o que prova que |a| ≥ |d|.
Para provar o “d divide”, observe que como a e b são múltiplos de d, existem inteiros q1 e q2 tais que
a = dq1 e b = dq2 . Assim, ax + by = d · (q1 x + q2 y) e como q1 x + q2 y é inteiro, temos que ax + by é também
um múltiplo de d.
Os exemplos a seguir ilustram como aplicar estas duas propriedades para resolver problemas de divisibilidade:
Exemplo 4. Encontre todos os inteiros positivos a e b tais que
1 1
1
+ =
a b
6
Solução. Isolando a variável a (por exemplo) temos
1 1
1
b−6
6b
1
= −
⇐⇒
=
⇐⇒ a =
a
6 b
a
6b
b−6
Como queremos a > 0, devemos ter b > 6. Assim, o problema é equivalente a encontrar todos os valores
inteiros b ≥ 7 para os quais b − 6 | 6b. Utilizaremos para isto o “d divide” (neste caso o “b − 6 divide”) para
“simplificar” o 6b, reduzindo-o a uma constante:
(
b − 6 | 6b
=⇒ b − 6 | 6b · 1 + (b − 6) · (−6) ⇐⇒ b − 6 | 36
b−6|b−6
Assim, como b ≥ 7, temos que b − 6 é um divisor positivo de 36, isto é, b − 6 ∈ {1, 2, 3, 4, 6, 9, 12, 18, 36}.
6b
Para cada um destes valores, obtemos uma solução com a = b−6
inteiro, de modo que as soluções (a, b) são
(42, 7) (24, 8) (18, 9) (15, 10) (12, 12) (10, 15) (9, 18) (8, 24) (7, 42)
Observe que as soluções obtidas são simétricas em a e b, isto é, se (a, b) é uma solução então (b, a) também
é uma solução. Isto não é mera coincidência: a equação original já era simétrica em relação a a e b, logo
suas soluções devem manter esta propriedade!
Exemplo 5. Encontre todos os inteiros positivos n tais que
2n2 + 1 | n3 + n2 + 1
Solução. A estratégia aqui é utilizar o “d divide” para reduzir o grau da expressão n3 + n2 + 1 e em seguida
utilizar o “d menor”. Basta escolhermos uma combinação linear conveniente para cancelar o termo de maior
grau n3 :
(
2n2 + 1 | n3 + n2 + 1
=⇒ 2n2 + 1 | 2 · (n3 + n2 + 1) + (−n) · (2n2 + 1)
2n2 + 1 | 2n2 + 1
⇐⇒
2n2 + 1 | 2n2 − n + 2
2
Como o grau de 2n2 − n + 2 ainda é maior ou igual ao grau de 2n2 + 1, podemos aplicar mais uma vez o “d
divide”:
(
2n2 + 1 | 2n2 − n + 2
=⇒ 2n2 + 1 | (2n2 − n + 2) − (2n2 + 1)
2n2 + 1 | 2n2 + 1
⇐⇒
2n2 + 1 | −n + 1
Como o grau de −n + 1 é estritamente menor do que o grau de 2n2 + 1, a última relação impõe restrições
severas sobre os possı́veis valores de n, já que para valores suficientemente grandes de n um polinômio de
maior grau possui valor absoluto maior. Assim, utilizando o “d menor”, temos dois casos a analisar:
• −n + 1 = 0 ⇐⇒ n = 1, que é uma possı́vel solução, como mostra uma verificação direta na relação
de divisibilidade original;
• −n + 1 6= 0 e portanto 2n2 + 1 | −n + 1 implica que
|2n2 + 1| ≤ | − n + 1| ⇐⇒ 2n2 + 1 ≤ n − 1 ⇐⇒ 2n2 − n + 2 ≤ 0
(note que | − n + 1| = n − 1 pois n > 0 e assim −n + 1 ≤ 0). Esta última desigualdade não possui
soluções reais (e muito menos inteiras) já que o discriminante de 2n2 − n + 2 é ∆ = −15 < 0.
Logo a única solução é n = 1.
Exemplo 6. Encontre todos os inteiros a, b ≥ 2 para os quais
ab − 1
(a − 1)(b − 1)
é um inteiro.
Solução. Começamos fazendo uma “substituição psicológica” (que embora não altere em nada o problema,
torna-o aparentemente mais fácil, psicologicamente falando, é claro) cuja finalidade é “simplificar” o denominador da expressão acima:
(
(
x=a−1
a=x+1
⇐⇒
y =b−1
b=y+1
Assim, o problema é equivalente a encontrar inteiros x, y ≥ 1 para os quais a expressão
(x + 1)(y + 1) − 1
xy + x + y
x+y
=
=1+
xy
xy
xy
é um inteiro. Em outras palavras, devemos encontrar todos os inteiros positivos x, y tais que xy | x + y.
Como para x e y suficientemente grandes xy é maior do que x + y, novamente nos encontramos na situação
em que o “d menor” fornece fortes restrições para os possı́veis valores destas variáveis.
Por simetria, podemos nos restringir às soluções em que 1 ≤ x ≤ y. Neste caso, temos que
xy | x + y =⇒ xy ≤ x + y ≤ 2y =⇒ x ≤ 2
Assim, temos dois casos:
• x = 1 e assim y | y + 1, logo y | (y + 1) − y ⇐⇒ y | 1 ⇐⇒ y = 1 pelo “y divide”.
• x = 2 e neste caso 2y | y + 2, logo 2y | 2(y + 2) − 2y ⇐⇒ 2y | 4 ⇐⇒ y | 2 e como y ≥ x = 2 a única
possibilidade é y = 2, que claramente é uma solução.
3
Portanto as soluções (x, y) são (1, 1) e (2, 2), isto é, (a, b) = (2, 2) ou (a, b) = (3, 3).
Uma outra maneira de se chegar a estas soluções é a seguinte: observe que o quociente
1
1
x+y
= + ≤1+1=2
xy
x y
já que x, y ≥ 1. Logo, sendo este quociente inteiro, devemos ter x+y
xy = 1 ou
podem ser resolvidas utilizando a técnica do “d divide”, como no exemplo 4.
1.2
x+y
xy
= 2, equações estas que
Máximo Divisor Comum e Algoritmo de Euclides
Vamos começar relembrando algumas definições que você provavelmente já conhece da escola.
Definição 7. Se a e b são inteiros, com a 6= 0 ou b 6= 0, denotamos por
def
(a, b) = max{d tais que d | a e d | b}
(ou mdc(a, b) por ênfase) o maior divisor comum de a e b. Denotamos também por
def
mmc(a, b) = min{m tais que a | m e b | m}
o menor múltiplo comum positivo de a e b.
Note que não definimos (0, 0) pois o conjunto dos divisores comuns de 0 e 0 é o Z, logo não há maior
divisor comum!
Exemplo 8. Vejamos alguns exemplos.
• Temos que (9, 12) = 3, pois 3 é o maior dentre os divisores comuns de 9 e 12:
{±1, ±3, ±9} ∩ {±1, ±2, ±3, ±4, ±6, ±12} =
{z
} |
{z
}
|
divisores de 9
divisores de 12
{±1, ±3}
| {z }
divisores comuns
Da mesma forma, temos que mmc(9, 12) = 36. Note que mdc(9, 12) · mmc(9, 12) = 9 · 12. O fato que
isto não é uma coincidência será provado mais adiante no próximo capı́tulo.
• temos (a, b) = (b, a) > 0 para a e b não simultaneamente iguais a 0, pois se d é um divisor comum de
a e b, ele é um divisor comum de b e a (duh!) e, além disso, −d também é um divisor comum, sendo
que ou −d > 0 ou d > 0;
• para qualquer a 6= 0 temos (a, 0) = |a|, pois os divisores comuns de a e 0 são simplesmente os divisores
de a, dentre os quais |a| é o maior.
Definição 9. Se (a, b) = 1, dizemos que a e b são primos entre si. Em outras palavras, a e b são primos
entre si se eles não admitem divisores positivos comuns além do 1.

Não confunda esta definição com a noção de número primo, aqui a e b não precisam ser números
primos!
Já que tocamos no assunto, vamos aproveitar para definir
Definição 10. Um inteiro positivo p é chamado de primo se ele possui exatamente dois divisores positivos,
a saber 1 e p. Um inteiro positvo n é chamado de composto se ele pode ser escrito como produto n = ab de
dois inteiros a e b com 1 < a, b < n.
4

Ao contrário da crença popular, 1 não é primo. Ele também não é composto. Então o que ele é?
Ele é uma unidade, ora bolas! Embora possa parecer arbitrário à primeira vista, esta convenção
se mostra bastante razoável na prática pois caso admitı́ssemos 1 como primo, vários teoremas sobre primos
teriam que ser enunciados como “. . . válido para todo primo exceto 1. . . ”
Exemplo 11. Alguns exemplos.
• Os primeiros 10 primos são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Uma tabela com os primeiros 240 primos (e
suas raı́zes primitivas) encontra-se no final do livro;
• 12 e 35 são primos entre si, embora nenhum destes números seja primo;
• se p é um número primo, como os únicos divisores positivos de p são 1 e p, temos que
(
1 se p ∤ a
(p, a) =
p se p | a
• dois números consecutivos são sempre primos entre si: pelo “d divide”, um divisor comum d > 0 de n
e n + 1 necessariamente divide 1 = (n + 1) − n, logo d = 1;
• temos que se d = (a, b) então ad e db são primos entre si, pois se houvesse um divisor comum e > 1
destes dois números então ed seria um divisor comum de a e b estritamente maior do que d.
Agora vamos aplicar o que acabamos de ver para resolver um problema histórico: a primeira questão da
prova da primeira Olimpı́da Internacional de Matemática!
Exemplo 12 (IMO). Mostre que a fração
21n + 4
14n + 3
é irredutı́vel para todo n natural.
Solução. A fração acima é redutı́vel se existe um d > 1 que divide simultaneamente o numerador e o
denominador. Assim, mostrar que a fração é irredutı́vel é o mesmo que mostrar que qualquer inteiro positivo
d que divide simultaneamente 21n + 4 e 14n + 3 deve ser igual a 1, em outras palavras, devemos mostrar que
21n + 4 e 14n + 3 são primos entre si para qualquer n natural. Basta utilizar o nosso velho canivete suı́ço, o
“d divide”:
(
d | 21n + 4
=⇒ d | (−2) · (21n + 4) + 3 · (14n + 3) ⇐⇒ d | 1
d | 14n + 3
Como d > 0, devemos ter d = 1, como querı́amos.
Exemplo 13. Mostre que 216 + 1 e 232 + 1 são primos entre si.
Solução. Seja d um divisor comum positivo deste dois números. A ideia natural é tentar utilizar o “d
divide”, mas a dificuldade é encontrar a combinação linear correta. Imagine 216 + 1 e 232 + 1 como sendo
“polinômios na variável 2” e tentemos reduzir o “grau de 2”, como no exemplo 5:
(
d | 216 + 1
=⇒ d | 216 · (216 + 1) − (232 + 1) ⇐⇒ d | 216 − 1
d | 232 + 1
Como d | 216 + 1 e d | 216 − 1 temos que d divide a diferença 2, logo temos em princı́pio duas possibilidades:
d = 1 ou d = 2. Porém d não pode ser igual a 2, pois 2 não divide o número ı́mpar 216 + 1. Logo d = 1,
como querı́amos.
5
Calcular o mdc a partir da definição é uma tarefa inconveniente para números grandes (nem tão grandes
assim, como você já deve ter percebido). Felizmente há um algoritmo bastante eficiente para seu cálculo,
baseado no algoritmo da divisão que todos nós estudamos no primário! Destes saudosos tempos, sabemos
que dados dois inteiros positivos a e b, o algoritmo da divisão
b
q
a
r
produz dois inteiros q (quociente) e r (resto) tais que
a=b·q+r
e
0≤r<b
Para quaisquer dois inteiros a e b (possivelmente negativos) com b 6= 0, podemos estender a noção de
quociente q e resto r da divisão de a por b utilizando relações análogas às acima:
Definição 14. Dados dois inteiros a e b com b 6= 0, o quociente q e o resto r são os únicos dois inteiros
determinados pelas relações
a= b·q+r
e
0 ≤ r < |b|
(∗)
Denotamos o resto da divisão de a por b através da notação a mod b.
Exemplo 15. Temos a seguinte tabela para a = ±13 e b = ±3:
a
13
−13
13
−13
b
3
3
−3
−3
quociente q
4
−5
−4
5
resto r = a mod b
1
2
1
2
Para que a definição acima realmente faça sentido, devemos mostrar
Lema 16. Para quaisquer a e b com b 6= 0, os inteiros q e r na definição (∗) acima existem e estão
unicamente determinados.
Demonstração. Para mostrar a existência, considere o conjunto
. . . , −3|b|, −2|b|, −|b|, 0, |b|, 2|b|, 3|b|, . . .
dos múltiplos de |b| (que é igual ao conjunto dos múltiplos de b). O inteiro a encontra-se entre dois múltiplos
consecutivos de |b|, digamos k · |b| ≤ a < (k + 1) · |b|. Defina
(
k se b > 0
def
def
q =
e
r = a − k · |b| = a − b · q
−k se b < 0
Assim, temos a = b · q + r e como k · |b| ≤ a < (k + 1) · |b| =⇒ 0 ≤ a − k · |b| < |b| temos também 0 ≤ r < |b|,
como desejado.
Para demonstrar a unicidade, suponha que exista um outro par de inteiros q ′ e r′ satisfazendo a = b·q ′ +r′
e 0 ≤ r′ < |b|. Assim,
b · q + r = a = b · q ′ + r′ ⇐⇒ b · (q − q ′ ) = r′ − r
e portanto r′ − r é um múltiplo de b. Porém, como 0 ≤ r, r′ < |b|, temos que |r′ − r| < |b|. Mas o único
múltiplo de b com valor absoluto estritamente menor do que |b| é 0, logo r′ − r = 0, ou seja, r′ = r, e como
(∗) determina q unicamente uma vez conhecidos a, b, r, temos que q = q ′ , completando a demonstração.
Agora sim estamos prontos para descrever o algoritmo para o cálculo do mdc, o chamado algoritmo de
Euclides ou algoritmo das divisões sucessivas:
6
Teorema 17 (Algoritmo de Euclides). Sejam a e b inteiros com b 6= 0. Então
(a, b) = (b, a mod b)
Demonstração. Sejam q e r = a mod b o quociente e o resto da divisão de a por b. A fim de provar a
igualdade dos mdc’s acima, basta mostrar que os pares a, b e b, r possuem o mesmo conjunto de divisores,
pois em particular o maior deles será igual. Assim devemos mostrar que
(
(
d|a
d|b
⇐⇒
d|b
d|r
Basta utilizar o “d divide” duas vezes:
• (=⇒) Se d divide a e b então d também divide r = a − bq.
• (⇐=) Se d divide b e r então d também divide a = bq + r.
Exemplo 18. Aplicando reiteradamente o teorema acima, temos um procedimento eficiente para calcular o
mdc de dois inteiros grandes. Por exemplo, temos
(27889, 18937) =
=
1.3
(18937, 8952) = (8952, 1033) = (1033, 688) = (688, 345)
(345, 343) = (343, 2) = (2, 1) = (1, 0) = 1
O anel Z/mZ dos inteiros módulo m
No estudo da divisibilidade por um inteiro fixado m, é conveniente “classificar” todos os inteiros segundo os
seus restos na divisão euclidiana por m, uma espécie de “taxonomia” de Z. Para isto introduzimos a seguinte
Definição 19. Seja m um inteiro fixado. Para um inteiro a qualquer, definimos a classe de congruência de
a módulo m, denotada por a, como sendo o conjunto de todos os inteiros b que deixam o mesmo resto que
a na divisão euclidiana por m:
a
def
=
{b ∈ Z | b mod m = a mod m}
=
=
{mq + a | q ∈ Z}
{b ∈ Z | b − a é múltiplo de m}
Mostremos que as várias definições de a acima são, de fato, todas equivalentes entre si. Escreva a = mq0 +r
com r = a mod m. Note que os inteiros b que deixam resto r são exatamente os da forma b = mq ′ + r com
q ′ ∈ Z. Assim, b = mq ′ +(a−mq0 ) = m(q ′ −q0 )+a e quando q ′ percorre todos os inteiros, q = q ′ −q0 também
percorre todos os inteiros (lembre-se de que q0 é uma constante determinada por a, a saber o quociente de a
por m). Isto mostra a igualdade dos dois conjuntos da primeira e segunda linhas, enquanto que a igualdade
entre os conjuntos da segunda e terceira linhas é imediata.
Exemplo 20.
• se m = 2, temos
0
=
1
=
{. . . , −4, −2, 0, 2, 4, . . .}
{. . . , −3, −1, 1, 3, 5, . . .}
Assim, temos uma partição dos inteiros Z em duas classes, 0 (popularmente conhecidos como pares)
e 1 (vulgo ı́mpares). Assim, no que tange à divisibilidade por m = 2, há somente dois “tipos” ou
“classes” de inteiros;
7
• No exemplo anterior, temos 0 = 4 = (−2) e 1 = 3 = (−101), de modo que poderı́amos indistintamente
escrever a partição de Z acima como Z = 0 ∪ 1 ou Z = 4 ∪ (−101), por exemplo;
• para m = 3, há três “tipos” ou classes de inteiros módulo 3: os que deixam resto 0, os que deixam
resto 1 e os que deixam resto 2 na divisão euclidiana por 3.
0 =
1 =
2 =
{. . . , −3, 0, 3, 6, . . .}
{. . . , −2, 1, 4, 7, . . .}
{. . . , −1, 2, 5, 8, . . .}
• Em geral, há precisamente m classes de inteiros módulo m, agrupados nos conjuntos 0, 1, 2, . . . , m − 1
segundo os m possı́veis restos 0, 1, 2, . . . , m − 1 na divisão euclidiana por m;
• note que, para qualquer m e a, o conjunto a é uma progressão aritmética de razão m (infinita para
ambos os lados) que contém a;
Um fato notável, e que é a razão pela qual introduzimos a definição acima, é a compatibilidade das
operações aritméticas de soma, diferença e produto com a partição de Z em classes módulo m:
Z = 0 ∪ 1 ∪2 ∪ ···∪ m − 1
Para entender o que isto significa, vejamos um exemplo para m = 5. Neste caso as classes módulo 5 são
0
1
2
3
4
= {. . . , −10, −5, 0, 5, 10, . . .}
= {. . . , −9, −4, 1, 6, 11, . . .}
= {. . . , −8, −3, 2, 7, 12, . . .}
= {. . . , −7, −2, 3, 8, 13, . . .}
= {. . . , −6, −1, 4, 9, 14, . . .}
Veja que se somarmos um elemento de 2 com outro de 4 sempre obtemos um elemento de 2 + 4 = 6 = 1.
Por exemplo, tome 7 ∈ 2 e −1 ∈ 4, temos que 7 + (−1) = 6 ∈ 1. Ou 12 ∈ 2 e 4 ∈ 4, temos 12 + 4 = 16 ∈ 1.
Ou ainda −3 ∈ 2 e −1 ∈ 4, temos (−3) + (−1) = −4 ∈ 1. Em outras palavras, a partição acima é compatı́vel
com a soma.
Mais ainda, ela também é compatı́vel com o produto: por exemplo, multiplicando um elemento de 2 com
outro de 4 sempre obtemos um elemento de 2 · 4 = 8 = 3. Vamos fazer um experimento: tome −3 ∈ 2 e
9 ∈ 4, temos que (−3) · 9 = −27 ∈ 3 (uau, não é que funciona mesmo!).
Chega de experimentos; é hora de provarmos
Lema 21 (Compatibilidade com operações aritméticas). Fixe um inteiro m. Para quaisquer dois elementos
i∈a
e
j∈b
pertencentes às classes de a e b módulo m, temos que
i+j ∈a+b
Em outras palavras, temos
(
i=a
j=b
i−j ∈a−b
i·j ∈a·b


i + j = a + b
=⇒ i − j = a − b


i·j = a·b
8
Demonstração. Começamos observando que pela definição
(
(
m|i−a
i∈a
⇐⇒
j∈b
m|j−b
(∗)
Logo, pelo “m divide”,
m | (i − a) + (j − b) ⇐⇒ m | (i + j) − (a + b) ⇐⇒ i + j ∈ a + b
Analogamente mostra-se que i − j ∈ a − b. Finalmente, novamente pelo “m divide” temos que (∗) implica
m | j · (i − a) + a · (j − b) ⇐⇒ m | i · j − a · b ⇐⇒ i · j ∈ a · b
O lema acima permite definir a operações com as classes da seguinte forma. Por exemplo, a soma de
duas classes a e b é feita tomando-se qualquer elemento i de a, qualquer elemento j de b e definindo a soma
a + b como sendo a classe que contém i + j. O lema nos garante que esta definição não depende de quais
“representantes” de classe i e j foram escolhidos. Podemos, por exemplo, tomar i = a e j = b, e neste caso
as definições podem ser descritas sucintamente através das equações
def
def
a + b = a + b,
a − b = a − b,
def
a·b = a·b
Em particular, observe que para n natural temos
def
n ·a = a+ a + ···+ a = n ·a
|
{z
}
n vezes
e
def
(a)n = |a · a ·{z. . . · a} = (an )
n vezes
Definimos também
def
−a = (−a)
de modo que (−a) + a = a + (−a) = 0.
Hora de fazer contas! Mas com isso você já contava. . .
Exemplo 22. Temos as seguintes tabelas de adição e multiplicação para as classes módulo m = 6:
+
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
1
2
3
4
5
0
2
3
4
5
0
1
3
4
5
0
1
2
4
5
0
1
2
3
5
0
1
2
3
4
·
0
1
2
3
4
5
e
0
1
2
3
4
5
0
0
0
0
0
0
0
1
2
3
4
5
0
2
4
0
2
4
0
3
0
3
0
3
0
4
2
0
4
2
0
5
4
3
2
1
Observe que estas operações nada mais são do que as operações usuais nos inteiros, somente que elas são
realizadas no ciclo de perı́odo m = 6:
2
1
3
0
4
5
9
Por exemplo, para somar 4 com 3, fazemos a operação em inteiros 4 + 3 = 7 e depois percorremos o ciclo a
partir do 0 em “7 unidades”, obtendo o resultado 1. Naturalmente, isto nada mais é do que uma interpretação
pictória da igualdade 7 = 1, que corresponde a tomar o resto de 7 na divisão por 6.
Exemplo 23. Calcule, em função do número natural n, o resto de 2n na divisão por 31.
Solução. Em outras palavras, devemos encontrar, em função de n, a classe de congruência de 2n módulo 31.
n
n−1
, podemos calcular estas potências “recursivamente”, aproveitando o valor anterior:
Como 2n = 2 = 2 · 2
0
2
1
2
2
2
3
2
4
2
=
=
=
=
=
5
1
2·1
2·2
2·4
2·8
=
=
=
=
2
6
2
7
2
8
2
9
2
2
4
8
16
= 2 · 16
= 2·1
= 2·2
= 2·4
= 2·8
0
= 32 =
= 2
= 4
= 8
= 16
1
...
5
E aı́, percebeu um padrão? A partir da repetição 2 = 2 , estabeleceu-se um ciclo de perı́odo 5. Assim, para
todos os n divisı́veis por 5 temos 2n = 1, para todos os n da forma n = 5k + 1 (ou seja, aqueles que deixam
resto 1 na divisão por 5) temos 2n = 2, etc. Portanto a resposta final é


1 se n é da forma n = 5k





2 se n é da forma n = 5k + 1
2n mod 31 = 4 se n é da forma n = 5k + 2



8 se n é da forma n = 5k + 3



16 se n é da forma n = 5k + 4
Exemplo 24. Calcule o resto da divisão de 122001 por 97.
Demonstração. Nossa missão aqui é determinar a qual das classes de congruência 0, 1, 2, · · · , 96 módulo 97
o número 121000 pertence. A estratégia é ir fazendo as contas “aos pouquinhos”, sempre “reduzindo” o
resultado.
Temos que uma potência de 12 “próxima” de 97 é 122 = 144. Assim,
2
12 = 144 = 47
Elevando ao quadrado, temos
4
2
12 = 47 = 2209 = 75
Muito bom! Já sabemos que 124 deixa resto 75 na divisão por 97 sem precisar calcular 124 explicitamente!
Esta ideia parece promissora. Vamos tentar mais uma vez:
8
12
=
2
75
=
↑
(−22)2
=
484 =
96
truque do “complementar”
Aqui utilizamos um artifı́cio para simplificar as contas: em vez de utilizar o “representante” 75 ∈ 75,
é mais fácil calcular o quadrado do igualmente válido representante −22 ∈ 75 (a quem apelidamos de
8
“complementar” de 75 módulo 97 já que 22 + 75 = 97). Mas agora, pelo mesmo truque, temos 12 = 96 = −1
e nada mais fácil do que calcular potências de −1! (bem, calcular potências de 1 é um pouco mais fácil mas
enfim, como diz o velho ditado, −1 dado não se olha nos dentes. . . )
8
2000
Agora rapidamente terminamos o problema: elevando 12 = −1 a 250, obtemos 12
= 1. Finalmente
2001
= 12, isto é, 122001 mod 97 = 12.
multiplicando por 12, obtemos a resposta final 12
10
O próximo exemplo mostra como a utilização de classes de congruência pode reduzir um problema a
analisar apenas um número finito de casos.
Exemplo 25. Mostre que n5 − n é um múltiplo de 5 para qualquer inteiro n.
Solução. Mostrar que n5 − n é múltiplo de 5 é mostrar que n5 − n está na classe de congruência do 0, isto
é, devemos mostrar que, para qualquer n, n5 − n = 0. Temos
n5 − n = (n5 ) − n = (n)5 − n
Mas para n só há um número finito de possibilidades, a saber 0, 1, 2, 3, 4. Assim, o problema, que antes
dispunha sobre um número infinito de possı́veis valores para n, agora se reduz a um número finito de
verificações! Temos (utilizando o “truque do complementar” 3 = −2 e 4 = −1 para simplificar as contas)
n=0
n=1
=⇒ (n)5 − n = (0)5 − 0 = 0 − 0 = 0
=⇒ (n)5 − n = (1)5 − 1 = 1 − 1 = 0
n = 2 =⇒ (n)5 − n = (2)5 − 2 = 32 − 2 = 2 − 2 = 0
n = −2 =⇒ (n)5 − n = (−2)5 − (−2) = − (2)5 − 2 = 0
n = −1 =⇒ (n)5 − n = (−1)5 − (−1) = − (1)5 − 1 = 0
Logo n5 − n = (n)5 − n é sempre igual a 0, independentemente do valor de n, como desejado.
Terminamos esta seção com uma pequena
Definição 26. Fixado m, o conjunto
{0, 1, 2, . . . , m − 1}
de todas as classes de congruência módulo m, juntamente com as operações de soma e produto acima definidos, é chamado de anel de inteiros módulo m, e é denotado por Z/mZ ou simplesmente Z/m.

Em Matemática, anel é o nome dado a qualquer conjunto A com duas operações binárias + (soma) e
· (produto) satisfazendo axiomas que abstraem as propriedades usuais das mesmas operações sobre
os inteiros (por exemplo). Estes axiomas são
• (associatividade da soma) (a + b) + c = a + (b + c) para todo a, b, c ∈ A;
• (elemento neutro da soma) existe um elemento 0 ∈ A tal que a + 0 = 0 + a = a para todo a ∈ A;
• (inverso da soma) para todo a ∈ A existe um b ∈ A tal que a + b = b + a = 0;
• (comutatividade da soma) a + b = b + a para todo a, b ∈ A;
• (associatividade do produto) (a · b) · c = a · (b · c) para todo a, b, c ∈ A;
• (elemento neutro do produto) existe um elemento 1 ∈ A tal que 1 · a = a · 1 = a para todo a ∈ A;
• (distributividade) a · (b + c) = a · b + a · c e (a + b) · c = a · c + b · c para todo a, b, c ∈ A.
Um outro exemplo de anel que você já pode ter visto é o anel de todas as matrizes n × n com entradas
reais, com a soma e o produto usual de matrizes. Aqui, os elementos neutros da soma e do produto são as
matrizes nula e identidade, respectivamente. Note que o produto neste anel não é comutativo.
11
1.4
A Relação de Congruência módulo m
A notação a para a classe de congruência de a módulo m possui o inconveniente de que o módulo m
não aparece explicitamente. Além disso, como vimos nos problemas acima, em muitas questões estamos
interessados em apenas decidir se a = b para duas classes a e b. Por isso introduzimos a seguinte
Definição 27. Dizemos que a é congruente a b módulo m e escrevemos
a ≡ b (mod m)
se, e somente se, a e b pertencem à mesma classe de congruência módulo m, isto é, se e somente se,
a ≡ b (mod m)
⇐⇒
⇐⇒
⇐⇒
⇐⇒
a=b
a mod m = b mod m
a = mq + b para algum q
m | (a − b)
Em particular, se r = a mod m é o resto da divisão de a por m, então a ≡ r (mod m).
Exemplo 28. Temos que
• 35 ≡ 11 (mod 12) pois 12 | 35 − 11 (em outras palavras, as classes 35 e 11 de congruência módulo
12 são iguais). Da mesma forma, 5 ≡ −19 (mod 12) pois 5 − (−19) = 24 é um múltiplo de 12 ou,
equivalentemente, 5 e −19 deixam o mesmo resto 5 quando divididos por 12;
• m | a ⇐⇒ a = 0 ⇐⇒ a ≡ 0 (mod m).
A notação de congruência foi introduzida pelo grande matemático alemão Johann Carl Friedrich Gauß
(1777–1855) em sua obra Disquisitiones Arithmeticae (caso seu Latim esteja enferrujado, a tradução para o
Português é Indagações Aritméticas). A definição de congruências aparece logo no primeiro parágrafo desta
importante obra:
“Si numerus a numerorum b, c differentiam metitur, b et c secundum a congrui dicuntur, sin
minus, ingongrui; ipsum a modulum appellamus. Uterque numerorum b, c priori in casu alterius
residuum, in posteriori vero nonresiduum vocatur.” 1
A relação de congruência tem propriedades muito semelhantes às da relação de igualdade: quando escrevemos a ≡ b (mod m), como a = b, em termos de questões de divisibilidade por m os inteiros a e b são por
assim dizer “equivalentes”. Matemáticos gostam de expressar este fato dizendo que a relação de congruência
é uma relação de equivalência.
Definição 29. Seja X um conjunto e ∼ uma relação binária em X. Dizemos que ∼ é uma relação de
equivalência se ela satisfaz os seguintes 3 axiomas:
1. (Reflexividade) a ∼ a para todo a ∈ X.
2. (Simetria) se a ∼ b então b ∼ a.
3. (Transitividade) se a ∼ b e b ∼ c então a ∼ c.
1 Tradução livre: “Se o número a divide a diferença de dois números b e c, b e c são ditos congruentes com relação à a, senão
incongruentes; a é chamado módulo. Ambos os números b e c são chamados de resı́duos no primeiro caso e de não resı́duos no
segundo.”
12
Por exemplo, a relação de igualdade em Z é de equivalência. Outro exemplo: se X é o conjunto de objetos
de uma sala, então a relação
x ∼ y ⇐⇒ o objeto x têm a mesma cor do objeto y
é uma relação de equivalência (aqui estamos supondo que todos os objetos são monocromáticos, então para
nós não existe a mesa verde com pés azuis!). Ainda um terceiro exemplo: se X é o conjunto de cartas de
um baralho, defina x ∼ y se, e somente se, as duas cartas têm o mesmo naipe.
Os exemplos acima são casos particulares do seguinte fato: uma partição de X em conjuntos (dois a dois
disjuntos) Xi define uma relação de equivalência ∼ em X via x ∼ y ⇐⇒ x e y pertencem ao mesmo conjunto
Xi . No primeiro exemplo, a relação de igualdade corresponde à partição de Z em conjuntos unitários:
Z = · · · ∪ {−2} ∪ {−1} ∪ {0} ∪ {1} ∪ {2} ∪ · · ·
No segundo exemplo, temos a partição dos objetos segundo suas cores. E no terceiro exemplo, a partição
do baralho em 4 conjuntos segundo seus naipes. Como a relação de congruência é definida por a ≡ b
(mod m) ⇐⇒ a e b pertencem à mesma classe de congruência módulo m, temos que ≡ é a relação de
equivalência em Z correspondente à partição
Z = 0 ∪ 1 ∪2 ∪ ···∪ m − 1
O fato da relação de congruência ser de equivalência é interessante, mas até aı́ nada de impressionante,
afinal há uma multidão de relações de equivalência pelo mundo afora, qualquer partição de Z daria origem
a uma. O que é notável, e que foi a grande sacada do Gauß, é o fato de que essa relação de equivalência é
compatı́vel com as operações aritméticas usuais. Resumimos esta discussão no seguinte
Teorema 30 (Congruências: propriedades operacionais).
1. (Relação de equivalência) Para um m fixado, a relação de congruência módulo m é de equivalência,
ou seja, satisfaz
(i) (Reflexividade) a ≡ a (mod m) para todo a.
(ii) (Simetria) se a ≡ b (mod m) então b ≡ a (mod m).
(iii) (Transitividade) se a ≡ b (mod m) e b ≡ c (mod m) então a ≡ c (mod m).
2. (Compatibilidade com soma, diferença e produto) Suponha que
a≡b
(mod m)
e
c≡d
(mod m)
Então
a+c
a−c
a·c
≡
≡
≡
b + d (mod m)
b − d (mod m)
b · d (mod m)
(1.1)
(1.2)
(1.3)
Em particular, temos
na
an
≡
≡
nb (mod m)
para todo n inteiro
(1.4)
bn
para todo n natural
(1.5)
(mod m)
3. (Cancelamento) Se (n, m) = 1 então
na ≡ nb (mod m) =⇒ a ≡ b
ou, equivalentemente,
n · a = n · b =⇒ a = b
13
(mod m)

Mas atenção, o cancelamento só vale quando (n, m) = 1!
Demonstração. Já demonstramos 1 e provaremos 3 no próximo capı́tulo (listamos esta propriedade aqui
por praticidade apenas). Finalmente, 2 é apenas a tradução do lemma 21 na relação de congruências: por
exemplo, para mostrar 1.1 note que, por hipótese, temos a = b e c = d então
a+c=a+c=b+d=b+d
e assim a + c ≡ b + d (mod m).
As propriedades operacionais nos dizem que a relação de congruência módulo m funciona “quase” como
se fosse a relação de igualdade, pois podemos somar, subtrair e multiplicar congruências, e mesmo “dividir”
em certas situações.
Exemplo 31. Mostre que se n é inteiro positivo ı́mpar então 2n + 1 é um múltiplo de 3.
Solução. Temos 2 ≡ −1 (mod 3). Como n é ı́mpar, elevando a n ambos os lados (propriedade 1.5) obtemos
2n ≡ (−1)n
(mod 3) ⇐⇒ 2n ≡ −1 (mod 3)
Somando com a congruência 1 ≡ 1 (mod 3) (simetria e propriedade 1.1), obtemos
2n + 1 ≡ 0 (mod 3) ⇐⇒ 3 | (2n + 1)
que era o que querı́amos provar. Veja que, na prática, o que fizemos foi nada mais nada menos do operar
com as congruências como em uma equação, elevando os dois lados a um mesmo expoente e “passando para
o outro lado” o −1, como em uma igualdade.
O exemplo acima ilustra o fato de que, ao calcularmos an mod m, é interessante procurar um expoente
d tal que ad ≡ ±1 (mod m). No capı́tulo 3 veremos uma fórmula para tal expoente, mas por hora fica a
mensagem:
≡♥±1
Exemplo 32. Calcule o resto da divisão de 22002 por 101.
Solução. Aqui, procedemos como em 24. Para calcular 22002 mod 101, começamos com uma potência de
2 “próxima” de 101, por exemplo 27 = 128. Elevando ao quadrado várias vezes e utilizando o “truque do
complementar”, obtemos
27 ≡ 27 (mod 101) =⇒ 214 ≡ 729 (mod 101) ⇐⇒ 214 ≡ 22 (mod 101)
=⇒ 228 ≡ 484 (mod 101) ⇐⇒ 228 ≡ −21 (mod 101)
=⇒ 256 ≡ 441 (mod 101) ⇐⇒ 256 ≡ −64 (mod 101)
Mas 64 = 26 , o que nos dá a oportunidade de aplicar nossa nova ferramenta, o cancelamento:
256 ≡ −26
(mod 101) =⇒ 250 ≡ −1 (mod 101)
E providencialmente encontramos 250 ≡ −1 (mod 101)! Agora é fácil terminar: dividindo 2002 por 50,
obtemos 2002 = 50 · 40 + 2 e assim
40 2
· 2 =⇒ 22002 ≡ (−1)40 · 22 (mod 101) ⇐⇒ 22002 ≡ 4 (mod 101),
22002 = 250
ou seja, 22002 ≡ 4 (mod 101). Logo o resto da divisão de 22002 por 101 é 4.
14
Exemplo 33. Calcule (3200 − 1, 335 − 1).
Solução. A ideia natural para calcular o mdc acima é utilizar o algoritmo de Euclides, que é o que vamos
fazer! Primeiramente temos que
(3200 − 1, 335 − 1) = (335 − 1, 3200 − 1 mod 335 − 1)
e assim devemos calcular 3200 − 1 mod 335 − 1. Pela filosofia ≡ ♥ ± 1 devemos encontar uma potência de
3 que é congruente a ±1 módulo 335 − 1, mas neste caso temos um candidato natural:
335 ≡ 1 (mod 335 − 1)
Dividindo 200 por 35 obtemos 200 = 35 · 5 + 25, logo
3200 = (335 )5 · 325
=⇒ 3200 ≡ 15 · 325 (mod 335 − 1)
=⇒ 3200 − 1 ≡ 325 − 1 (mod 335 − 1)
Como 0 ≤ 325 − 1 < 335 − 1, temos que 325 − 1 é o resto da divisão de 3200 − 1 por 335 − 1. Agora devemos
calcular
(335 − 1, 325 − 1) = (325 − 1, 335 − 1 mod 325 − 1)
Com o mesmo procedimento acima, obtemos após algumas contas (verifique!) que 335 − 1 mod 325 − 1 =
310 − 1. Assim, aplicando reiteradamente este processo temos
(335 − 1, 325 − 1) = (325 − 1, 310 − 1) = (310 − 1, 35 − 1) = 35 − 1
pois 310 − 1 = (35 − 1)(35 + 1) é múltiplo de 35 − 1. Logo (3200 − 1, 335 − 1) = 35 − 1.
Vejamos um exemplo em que congruências nos ajudam a provar a inexistência de soluções.
Exemplo 34. Mostre que se n ≡ 3 (mod 4) então n não pode ser escrito como soma de dois quadrados
perfeitos.
Solução. Suponha que n = x2 + y 2 . O ponto crucial aqui é notar que não há muitos “quadrados perfeitos
módulo 4”. Analisando todas as possibilidades, temos
x=0
=⇒ x2 = 0
x = ±1 =⇒ x2 = 1
x = 2 =⇒ x2 = 0
Assim, um quadrado perfeito só deixa resto 0 ou 1 módulo 4. Portanto
x2 + y 2 mod 4 ∈ {0, 1, 2}
Mas como n mod 4 = 3 não está no conjunto acima, não podemos ter n = x2 + y 2 .
Terminamos com uma simples
Definição 35. Um conjunto de m números inteiros
a1 , a2 , . . . , am
é chamado de sistema completo de resı́duos (ou restos) se ai 6≡ aj (mod m) para i 6= j, ou seja, se os
números ai representam todos os elementos de Z/mZ exatamente uma vez:
Z/mZ = {a1 , a2 , . . . , an }
15
1.5
Algumas aplicações
Vamos agora mostrar algumas aplicações dos conceitos vistos nas seções anteriores em problemas que aparecem na “natureza”.
1.5.1
Bases Numéricas (vulgo Problemas com Dı́gitos)
Um dos temas mais populares em olimpı́adas de Matemática são os bons e velhos “problemas com dı́gitos”.
O enunciado destes problemas muitas vezes mascaram fatos bem conhecidos da teoria dos Números, então é
importante familiarizar-se com eles.
Dado um número natural n, podemos “expandı́-lo” em base 10 como
n = ad · 10d + ad−1 · 10d−1 + · · · + a1 · 10 + a0
(∗)
com dı́gitos ai ∈ {0, 1, 2, . . . , 9}. Por exemplo,
19785 = 1 · 104 + 9 · 103 + 7 · 102 + 8 · 101 + 5 · 100
Muitos problemas com dı́gitos se resumem a escrever a expansão (∗). Por exemplo, os velhos critérios de
divisibilidade por 9 e 10 nada mais são do que uma aplicação imediata do nosso princı́pio ≡ ♥ ± 1 .
Exemplo 36 (critérios de divisibilidade por 9 e 11). Seja
n = ad · 10d + ad−1 · 10d−1 + · · · + a1 · 10 + a0
0 ≤ ai ≤ 9
a expansão do número natural n na base 10. Então
1. n tem o mesmo resto na divisão por 9 que a soma de seus dı́gitos a0 + a1 + · · · + ad . Em particular,
9 | n ⇐⇒ 9 | (a0 + a1 + · · · + ad );
2. n tem o mesmo resto na divisão por 11 que a soma alternada de seus dı́gitos a0 − a1 + a2 − · · · ± ad
(começando sempre pelo dı́gito da unidades). Em particular, 11 | n ⇐⇒ 11 | (a0 − a1 + a2 − · · · ± ad ).
Solução. Como 10 ≡ 1 (mod 9) e 10 ≡ −1 (mod 11) temos
n
n
≡
≡
ad · 1d + ad−1 · 1d−1 + · · · + a1 · 1 + a0 (mod 9)
ad · (−1)d + ad−1 · (−1)d−1 + · · · + a1 · (−1) + a0
(mod 11)
e o resultado segue.
Um problema bastante comum é o de determinar os “últimos” dı́gitos de uma potência grande. Neste
caso, o fato principal a ser utilizado é o seguinte: suponha que você queira encontrar os dois últimos dı́gitos
a0 de a1 de n em (∗). Como
n = (ad−2 · 10d−2 + ad−3 · 10d−3 + · · · + a3 · 10 + a2 ) · 102 + (10a1 + a0 )
e 0 ≤ 10a1 + a0 ≤ 10 · 9 + 9 < 100, temos que 10a1 + a0 é o resto da divisão de n por 102 = 100, logo o
problema se resume a calcular n mod 100. Caso você queira os três últimos dı́gitos, basta calcular n mod 103
e assim por diante.
Exemplo 37. Determine os dois últimos dı́gitos de 32009 .
Solução. Vamos calcular 32009 mod 100. Fazendo as contas módulo 100, temos
4
Portanto, de 3
10
8
10
3 = −19 =⇒ 3 = (−19)2 = 61 =⇒ 3
= 49 obtemos
3
20
2
= 3 · 61 = 49
2
= 49 = 1 =⇒ 32000 = 1
8
9
2009
Já calculamos 3 = 61, logo multiplicando por 3 obtemos 3 = 83. Logo 3
últimos dı́gitos de 32009 são 83.
16
9
= 1 · 3 = 83. Assim, os dois
Em alguns problemas, devemos também estimar a quantidade de dı́gitos de n. Isto é simples: como um
número n tem d dı́gitos se, e somente se, ele é maior ou igual a 10d−1 (menor número com d dı́gitos) e
estritamente menor do que 10d (menor número com d + 1 dı́gitos), e como o logarı́tmo na base 10 é uma
função crescente, concluı́mos que
10d−1 ≤ n < 10d =⇒ d − 1 ≤ log10 n < d =⇒ d = ⌊log10 n⌋ + 1
onde, para um número real x, ⌊x⌋ denota a parte
√ inteira t de x, isto é, o único inteiro t tal que x − 1 < t ≤ x.
Por exemplo, ⌊2,1⌋ = 2, ⌊π⌋ = 3, ⌊3⌋ = 3 e ⌊− 2⌋ = −2 (não é −1!). Resumindo
Lema 38 (Número de dı́gitos). Seja n um natural. Então o número de dı́gitos de n é igual a ⌊log10 n⌋ + 1.
Vejamos como aplicar esta ideia juntamente com as anteriores no seguinte
Exemplo 39. (IMO) Seja A a soma dos dı́gitos de 44444444 e B a soma dos dı́gitos de A. Ache a soma
dos dı́gitos de B.
Solução. Este problema pode impressionar à primeira vista, mas de fato ele é mais simples do que aparenta.
O ponto chave aqui é perceber que a operação “soma dos dı́gitos” fazer encolher tremendamente o seu
argumento!
Por exemplo, embora 44444444 seja gigantesco, como 44444444 < (104 )4444 = 1017776 , temos que 44444444
tem no máximo 17776 algarismos e portanto a soma A de seus dı́gitos não ultrapassa 17776 · 9 = 159984,
um número minúsculo quando comparado a 44444444 ! (sem o fatorial, é claro).
Como A ≤ 159984, temos que a soma B de seus dı́gitos não ultrapassa 9 + 9 + 9 + 9 + 9 = 45. De
fato, este é o pior dos casos para A < 105 ; no caso em que 105 ≤ A ≤ 159999, terı́amos no máximo
B ≤ 1 + 5 + 9 + 9 + 9 + 9 = 42 e 42 < 45.
Assim, B ≤ 45 e a soma C dos dı́gitos de B portanto não ultrapassa 3 + 9 = 12. Mas como encontrar
C exatamente? Aı́ entram as congruências: utilizando o critério de divisibilidade por 9, sabemos que a
operação “soma dos dı́gitos” não altera a classe de congruência módulo 9. Como
44444444 ≡ (4 + 4 + 4 + 4)4444
(mod 9) ⇐⇒ 44444444 ≡ (−2)4444
(mod 9)
e (−2)4444 ≡ 7 (mod 9) (verifique, utilize o fato que (−2)3 ≡ 1 (mod 9)) concluı́mos que o resto da divisão
de 44444444 por 9, bem como os restos das divisões de A, B e C por 9, são todos iguais a 7. Mas 0 < C ≤ 12,
logo a única possibilidade é C = 7, que é a soma procurada.
1.5.2
Usando congruências para resolver equações diofantinas
As congruências são extremamente úteis na resolução de equações em inteiros. Tais equações são chamadas
de diofantinas, em homenagem ao matemático grego Diofanto de Alexandria (∆ιóϕαντ oς ò Áλǫξανδρǫν́ς),
que viveu no século III D.C. e escreveu uma série de livros entitulados Arithmetica sobre resoluções de
equações algébricas.
Exemplo 40. (OBM) Determine todos os inteiros positivos m e n tais que
m2 + 161 = 3n
Solução. Começamos com um caso particular: suponha que n = 2k seja par. Mas por que estudar este
caso primeiro? Porque agora vale a fatoração
m2 + 161 = 3n ⇐⇒ 161 = 32k − m2 ⇐⇒ 161 = (3k − m)(3k + m)
Pois é, fatore e fature! Há um número finito de maneiras de escrever 161 como o produto de dois inteiros
3k − m e 3k + m. Utilizando o fato que 161 = 7 · 23 e que 3k − m < 3k + m temos somente dois casos:
(
(
3k − m = 1
3k − m = 7
e
k
3 + m = 161
3k + m = 23
17
(na verdade, aqui estamos nos adiantando um pouco porque utilizamos implicitamente o Teorema Fundamental da Aritmética sobre a fatoração única em primos, que será provado no próximo capı́tulo. . . )
No primeiro caso, resolvendo o sistema nas “variáveis” m e 3k obtemos m = 80 e 3k = 81 ⇐⇒ k = 4,
ou seja, (m, n) = (80, 8). No segundo caso, temos m = 15 e 3k = 8, que não possui soluções inteiras.
Será que a solução acima é a única? Para provar isto, vamos utilizar congruência para mostrar que n é
obrigatoriamente par. A primeira dúvida que poderia surgir é “que módulo vamos usar?” Aqui a ideia é
trabalhar módulo um número que “simplifique” a equação acima. Por exemplo, podemos tentar “apagar” o
161, e para isto escolhemos trabalhar módulo um de seus divisores, por exemplo 7:
m2 + 161 = 3n =⇒ m2 + 161 ≡ 3n
(mod 7) ⇐⇒ m2 ≡ 3n
(mod 7)
Em outras palavras, agora temos que comparar os possı́veis restos de m2 e 3n na divisão por 7. Como no
exemplo 23, as potências de 3 são periódicas módulo 7 com perı́odo 6:
1
3
2
6
4
5
0
6
12
1
7
13
3
9
15
5
11
= 3 =3 =3
= ···
= 3 = 3 = 3 = ···
2
8
14
= 3 = 3 = 3 = ···
= 3 = 3 = 3 = ···
4
10
16
= 3 = 3 = 3 = ···
= 3 =3
=3
17
= ···
Agora veja que há poucas possibilidades para os “quadrados perfeitos” m2 módulo 7; utilizando o truque do
complementar e analisando o número finito de casos, temos
m=0
=⇒ m2 = 0
m = ±1 =⇒ m2 = 1
n
m = ±2 =⇒ m2 = 4
m = ±3 =⇒ m2 = 2
Assim, para que m2 = 3 , devemos ter n = 6k (quando m2 = 1), n = 6k + 4 (quando m2 = 4) ou n = 6k + 2
(quando m2 = 2). Em todos os casos, n é par, logo a solução que encontramos acima é a única da problema.
Exemplo 41. Encontre todos os números naturais x e y tais que 2x = 3y − 1.
Solução. Aqui, qual o módulo? Você lembra do ≡ ♥ ± 1 ? Pois ele ataca novamente! Podemos, por
exemplo, trabalhar módulo 4, que é próximo de 3 e é uma potência de 2:
2x = 3y − 1 =⇒ 2x ≡ 3y − 1 (mod 4) ⇐⇒ 2x ≡ (−1)y − 1 (mod 4)
Agora precisamos analisar 2x mod 4. A grande maioria das potências de 2 é divisı́vel por 4, mas considerar
todas precisamos dividir em casos:
• se x = 0, temos 20 = 3y − 1 ⇐⇒ 3y = 2, o que não é possı́vel;
• se x = 1, temos 21 = 3y − 1 ⇐⇒ 3y = 3 ⇐⇒ y = 1, logo x = 1 e y = 1 é uma solução;
• se x ≥ 2 (caso geral), temos 2x ≡ 0 (mod 4). Logo devemos ter (−1)y − 1 ≡ 0 (mod 4), o que ocorre
se, e somente se, y é par. Assim, y = 2a, onde a é natural e voltando na equação original temos uma
fatoração:
2x = 32a − 1 ⇐⇒ 2x = (3a − 1)(3a + 1)
Como 3a − 1 e 3a + 1 são divisores de uma potência de 2, então 3a − 1 e 3a + 1 são ambas potências
de 2 pelo Teorema Fundamental da Aritmética (cuja demonstração veremos mais tarde, não perca o
18
próximo capı́tulo!). Mas a diferença entre elas é (3a + 1) − (3a − 1) = 2, e as únicas potências de 2 tão
“próximas” assim são 2 e 4. De fato, olhando para as potências de 2,
20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, . . .
observamos que se i > j e i ≥ 3 temos 2i − 2j ≥ 2i − 2i−1 = 2i−1 ≥ 22 = 4, logo devemos j ≤ i ≤ 2 e
agora analisando o número finito de possı́veis pares (i, j) temos que (i, j) = (1, 2) é a única possibilidade
viável.
Consequentemente, 3a − 1 = 2 ⇐⇒ a = 1 e logo y = 2 e x = 3.
Enfim, as únicas soluções são (x, y) = (3, 2) e (x, y) = (1, 1).
1.6
1.6.1
Exercı́cios
Básicos
1. Encontre todos os inteiros positivos tais que
(a) n + 1 | n3 − 1
1
1
(c) n1 + m
= 143
(b) 2n − 1 | n3 + 1
(d) 2n3 + 5 | n4 + n + 1
2. Mostre que
(a) 31 | 2015 − 1
(c) 641 | 232 + 1
(e) 7 | 22225555 + 55552222
(b) 61 | 2015 − 1
(d) 13 | 270 + 370
3. Determine o resto das divisões de
(a) 41234 por 3
(c) 2000 · 22000 − 1 por 3
(b) 20100 por 17
(d) 520 por 26
4. Encontre os dois últimos dı́gitos de
(a) 7100
(c) 5600 + 19200
18
5. Mostre que 8355 + 6
− 1 é divisı́vel por 112.
(b) 22000
(d) 72000 × 2300
√
6. Mostre que se n é um número natural composto, então n é divisı́vel por um primo p com p ≤ ⌊ n⌋.
7. Qual o número de dı́gitos de 20082008 quando escrito na notação decimal? (log10 2008 ≈ 3.302763 . . .)
1.6.2
Lição de Casa
8. Mostre que para todo natural n
(a) 7 | 23n+2 + 3
(c) 25 | 722n+2 − 472n + 282n−1
(b) 7 | 37n+2 + 16n+1 + 23n
(d) 24 | n(n2 − 1)(3n + 2)
9. Mostre que
(a) 215 − 1 e 210 + 1 são primos entre si.
(b) 232 + 1 e 24 + 1 são primos entre si.
10. Seja an = n2 + 100. Determine o maior valor possı́vel de (an , an+1 ).
11. Encontrar os 4 últimos dı́gitos de 32008 na notação decimal.
Dica: para reduzir as contas, aplique o binômio de Newton em (10 − 1)1004 .
19
12. Mostre que se m e n são dois inteiros positivos tais que mn + 1 é divisı́vel por 24 então m + n também
é divisı́vel por 24.
13. Encontre todos os números naturais de dois dı́gitos divisı́veis pela soma de seus dı́gitos.
14. Em cada casa do tabuleiro de xadrez, há o número de grãos de trigo indicado, como mostra a figura. O
cavalo de Bruno & Bernardo começa a se movimentar no tabuleiro, de acordo com as regras usuais, a partir
de uma casa qualquer. Quando ele atinge uma casa, come todos os grãos nela existentes (mas ele não come
os grãos da casa inicial). Quando ele deixa uma casa, nós recolocamos a mesma quantidade de grãos que
nela existiam. Depois de um certo tempo, o cavalo de Bruno & Bernardo retorna à casa inicial e come os
grãos nela existentes. Prove que o número de grãos que o cavalo de Bruno & Bernardo comeu durante sua
viagem é divisı́vel por 3
263 262 261 · · ·
216 217 218 · · ·
1.6.3
215 214 213 212 211 210 29
28
20
27
21
22
23
24
25
26
Questões de Provas
15. (IMO) Encontre todos os inteiros a, b, c com 1 < a < b < c tais que (a − 1)(b − 1)(c − 1) é divisor de
abc − 1.
16. Encontre os dois últimos dı́gitos de 22n (22n+1 − 1) para n ≥ 1 ı́mpar.
2009
17. Quais os dois últimos dı́gitos de 33
18.
?
(a) Mostre que 81 | 99
. . . 9} .
| {z
nove noves
(b) Determine o menor número da forma 99 . . . 9 que é divisı́vel por 17.
19. Mostre que 41 divide 11 . . . 1 (onde há 5k dı́gitos 1, k inteiro positivo).
20. Mostre que 91 divide 11 . . . 1 (onde há 6k dı́gitos 1, k inteiro positivo).
21. Mostre que, para todos k, m, n naturais, 55k+1 + 45m+2 + 35n é divisı́vel por 11.
22. Encontre todos os pares de inteiros positivos (x, y) tais que 2x = 1 + 3y .
23. Encontre todos os inteiros positivos x e y tais que 3x − 2y = 7.
20
Capı́tulo 2
Equações Diofantinas Lineares e
Teorema Fundamental da Aritmética
Uma equação diofantina linear (em duas variáveis) é uma equação da forma
ax + by = c
nas variáveis x e y. “Diofantina”, como você já sabe, se refere à qualquer equação em números inteiros,
enquanto que “linear” obviamente é uma referência ao fato de que a equação acima ser a de uma reta no
plano cartesiano.
Assim, resolver uma equação diofantina linear é o mesmo que encontrar todos os pontos inteiros (isto é,
com ambas as coordenadas inteiras) de uma reta. Por exemplo, tomando a reta
6x + 21y = 2
embora haja uma infinidade de pontos reais (e até mesmo racionais) não há nenhum ponto inteiro! De fato,
se x, y ∈ Z, o lado esquerdo é múltiplo de 3, enquanto que o direito não.
Neste capı́tulo, vamos aprender a reconhecer quando uma equação diofantina linear possui ou não solução
e, em caso afirmativo, como fazer para encontrar todas. Equações diofantinas lineares têm muitas aplicações
importantes: elas permitem provar, por exemplo, os teoremas do cancelamento para congruências e o Teorema
Fundamental da Aritmética sobre a decomposição única em primos.
2.1
Teorema de Bézout
O exemplo acima mostra uma obstrução óbvia para a existência de soluções inteiras de ax + by = c: se
houver um divisor comum d de a e b que não divide c então não há soluções inteiras. O teorema de Bézout
diz que, na ausência de tal obstrução, a equação admite solução.
Teorema 42 (Bézout). A equação
ax + by = c
admite solução se, e somente se, (a, b) | c.
Demonstração. Começamos com a implicação trivial: suponha que a equação admita solução, isto é, existem
x, y inteiros tais que ax + by = c. Como (a, b) divide o lado esquerdo da equação concluı́mos que (a, b) | c
também.
Reciprocamente, suponha que (a, b) | c. Basta mostrar que a equação
ax + by = (a, b)
21
tem solução, pois multiplicando uma solução desta equação por c/(a, b) obtemos uma solução da equação
original. Em outras palavras, devemos mostrar que (a, b) escreve-se como uma combinação linear de a e b.
Dentre todas as combinações lineares positivas ax+ by de a e b (existe pelo menos uma, verifique!), seja m
a menor, digamos m = ax0 + by0 . Observe que (a, b) | m pois (a, b) divide a e b e m é uma combinação linear
de a e b. Vamos mostrar agora que m divide qualquer combinação linear de a e b. Uma vez provado isto,
temos que, em particular, m é um divisor comum de a e b, logo m ≤ (a, b), que juntamente com (a, b) | m,
implica m = (a, b).
Seja t = ax + by uma combinação linear qualquer de a e b. Seja q e r o quociente e o resto da divisão de
t por m, de modo que t = qm + r com 0 ≤ r < m. Temos
r = t − qm = (ax + by) − q(ax0 + by0 ) = a(x − qx0 ) + b(y − qy0 )
Ou seja, o resto r também é uma combinação linear de a e b! Como r < m, pela minimalidade do m a única
possibilidade é r = 0, isto é, m | t, como desejado.
A prova do teorema acima não permite encontrar explicitamente uma solução de ax + by = c caso ela
exista. Porém isto pode ser facilmente feito utilizando-se o algoritmo de Euclides! Veja o
Exemplo 43 (Resolvendo Equações Diofantinas Lineares via Euclides). Encontre uma solução inteira de
1001x + 109y = 2.
Solução. Calculamos o mdc (1001, 109) via o algoritmo de Euclides:
1001
=
109 · 9 + 20
109
=
20 · 5 + 9
20
=
9 ·2+ 2
9
=
2 ·4+ 1
Assim, (1001, 109) = (109, 20) = (20, 9) = (9, 2) = (2, 1) = 1 e pelo teorema de Bézout a equação diofantina
linear acima possui solução.
Para encontrar uma, devemos expressar 2 como combinação linear de 1001 e 109. Note que a última
divisão permite expressar 1 como combinação linear de 9 e 2:
9 ·1− 2 ·4 = 1
Mas da penúltima divisão, temos que 2 = 20 − 9 · 2, logo substituindo esta expressão na combinação
linear acima temos
9 − ( 20 − 9 · 2) · 4 = 1 ⇐⇒ 9 · 9 − 20 · 4 = 1
e agora expressamos 1 como combinação linear de 20 e 9! Repetindo este procedimento, eventualmente
expressaremos 1 como combinação linear de 1001 e 109; multiplicando tudo por 2, obteremos então nossa
desejada solução!
Vamos fazer isto de modo mais sistemático: isolamos os restos no algoritmo de Euclides e fazemos as
substituições, partindo da última equação, e tomando o cuidado de lembrar quais são os “coeficientes” nas
equações durante as simplificações:
20
=
1001 − 109 · 9
9
=
109 − 20 · 5
2
=
20 − 9 · 2
1
=
9 − 2 ·4
22
e assim
1
=
9 − ( 20 − 9 · 2) · 4 = 9 · 9 − 20 · 4
1
= ( 109 − 20 · 5) · 9 − 20 · 4 = 109 · 9 − 20 · 49
1
=
109 · 9 − ( 1001 − 109 · 9) · 49 = 1001 · (−49) + 109 · 450
Portanto (x, y) = (−49, 450) é uma solução de 1001x + 109y = 1, logo multiplicando tudo por 2 temos que
(x, y) = (−98, 900) é uma solução de 1001x + 109y = 2.
O procedimento acima permite dar uma outra demonstração (da parte não trivial) do teorema de Bézout
via o princı́pio da indução finita (PIF). Vamos esboçá-la aqui quando a ≥ b > 0 e (a, b) = 1, deixando para
você completar os detalhes no caso geral. A indução é sobre min{a, b}.
Dividindo a por b, temos a = bq + r com 0 ≤ r < b. Temos que
ax + by = 1 ⇐⇒ (bq + r)x + by = 1 ⇐⇒ b(qx + y) + rx = 1
Como (a, b) = (b, r) = 1 e min{b, r} = r < b = min{a, b}, por hipótese de indução podemos encontrar
inteiros x0 e y0 para os quais bx0 + ry0 = 1. Logo, da equivalência acima, temos que x = y0 e y = x0 − qy0
é uma solução de ax + by = 1.
O teorema de Bézout não serve só para resolver equações diofantinas lineares; ele têm importantes
aplicações teóricas, como por exemplo o
Teorema 44 (Alternativa de primo). Se d | ab e (d, a) = 1 então d | b. Em particular, se p é um número
primo e
p | a 1 a 2 . . . an
então p | ai para algum i.
Demonstração. Pelo teorema de Bézout, existem x, y inteiros tais que ax + dy = 1. Multiplicando por b
temos
abx + bdy = b
Note d divide tanto abx (pois por hipótese d | ab) como bdy, logo d | b também, provando a primeira parte
do lema.
A segunda parte segue da primeira: se p não divide a1 , então p | a2 a3 . . . an . Agora, suponha que p não
divida a2 também. Terı́amos que p | a3 a4 . . . an . E assim por diante, de modo que enventualmente p terá
que dividir algum ai .
Podemos agora finalmente provar o
Corolário 45 (Cancelamento). Se (n, m) = 1 então
na ≡ nb
(mod m) =⇒ a ≡ b
(mod m)
ou, equivalentemente,
n · a = n · b =⇒ a = b
Demonstração. Note que
na ≡ nb (mod m) ⇐⇒ m | n(a − b)
Como (n, m) = 1, pela alternativa de primo temos que
m | a − b ⇐⇒ a ≡ b (mod m)
como desejado.
23
Podemos retornar agora às equações diofantinas lineares. Já sabemos identificar quando uma equação
destas possui solução e até mesmo encontrar uma. Como fazer para encontrar todas? Veja o
Exemplo 46. Encontre todas as soluções de 1001x + 109y = 2.
Solução. Vamos reescrever o lado direito utilizando a solução particular encontrada no exemplo anterior:
1001x + 109y = 2 = 1001 · (−98) + 109 · 900 ⇐⇒ 1001(x + 98) = −109(y − 900)
Como 1001 e 109 são primos entre si, pela alternativa de primo temos que 1001 divide y − 900, isto é,
y −900 = 1001t para algum t. Assim, substituindo na equação acima, temos 1001(x+98) = −109·1001t ⇐⇒
x + 98 = −109t, e as soluções são portanto
x = −98 − 109t
e
y = 900 + 1001t
com t ∈ Z.
Em outras palavras, os pontos inteiros da reta de equação 1001x + 109y = 2 são os pontos da forma
(x, y) = (−98, 900) + (−109, 1001)t para t ∈ Z, que estão igualmente espaçados na reta, sendo obtidos a
partir da translação do ponto inteiro (−98, 900) por múltiplos inteiros do vetor (−109, 1001).
2.2
Inverso Multiplicativo
Vimos como o cancelamento permite “dividir módulo m” sob certas circunstâncias. Nesta seção, queremos
tornar mais preciso este conceito de divisão módulo m:
Definição 47. Dado um elemento ā de Z/mZ, definimos o seu inverso multiplicativo, denotado por ā−1 ,
como sendo o elemento (caso exista) de Z/mZ tal que ā · ā−1 = 1̄.
−1
Por exemplo, como 7 · 13 ≡ 1 (mod 15) temos que 7
= 13 em Z/15Z.
Teorema 48. O elemento ā ∈ Z/mZ possui inverso multiplicativo se, e somente se, a é primo com m.
Demonstração. Note que o inverso multiplicativo x̄ de ā existe se, e somente se, a equação
ax ≡ 1 (mod m) ⇐⇒ ax − my = 1 para algum y
possui solução. E pelo teorema de Bézout, a equação diofantina linear acima é solúvel se, e somente se,
(a, m) = 1.
Assim, encontrar o inverso multiplicativo de ā ∈ Z/mZ é o mesmo que resolver a equação ax − my = 1,
−1
o que pode ser feito utilizando-se o algoritmo de Euclides. Assim, por exemplo, temos que 109 = 450 em
Z/1001.
De posse do inverso multiplicativo, temos agora todas as ferramentas para realmente tratar congruências
quase como uma relação de igualdade. Como exemplo, vamos resolver a seguinte equação:
Exemplo 49. Determine todos os inteiros x tais que
13x + 8 ≡ 6x + 11 (mod 15)
Solução. Isolando a variável x (i.e. subtraindo 6x + 8 de ambos os lados da congruência) obtemos
13x + 8 ≡ 6x + 11 (mod 15)
⇐⇒
⇐⇒
24
13x − 6x ≡ 11 − 8 (mod 15)
7x ≡ 3 (mod 15)
Agora gostarı́amos de “dividir por 7 módulo 15”. Mas isto é fácil! Basta multiplicar pelo inverso de 7 em
Z/15Z, ou seja, 13:
7x ≡ 3 (mod 15)
⇐⇒
⇐⇒
13 · 7x ≡ 13 · 3 (mod 15)
x≡9
(mod 15)
E voilá! Temos a resposta: todos os inteiros x tais que x ≡ 9 (mod 15), ou seja, todos os inteiros da forma
x = 9 + 15k para k ∈ Z.
Vamos ilustrar os conceitos acima provando o
Teorema 50 (Teorema de Wilson). Um natural p > 1 é primo se, e somente se, (p − 1)! ≡ −1 (mod p).
Demonstração. Suponha que p seja primo. Note que neste caso todos os elementos de Z/pZ, com exceção
de 0, são inversı́ves. Devemos provar que o produto (p − 1)! de todos estes inversı́veis é igual a −1 em Z/pZ.
Vamos ilustar a idea geral da prova com um caso particular primeiro. Por exemplo, para p = 11 podemos
formar “parzinhos”, cujos produtos são iguais a 1, isto é, parzinhos da forma {a, a−1 }:
{2, 6}
{3, 4}
{5, 9}
{7, 8}
Somente 1 e 10 = −1, que são seus próprios inversos, ficam “isolados”. Assim, temos
10! = 1 · 10 = −1
que era o querı́amos demonstrar.
No caso geral, observe que somente ±1 são seus próprios inversos pois pela alternativa de primo temos
x2 ≡ 1
(mod p)
⇐⇒
⇐⇒
p | x2 − 1 ⇐⇒ p | (x − 1)(x + 1)
p | x − 1 ou p | x + 1 ⇐⇒ x ≡ ±1 (mod p)
Assim, podemos agrupar os demais elementos em pares da forma {a, a−1 }, de modo que
(p − 1)! = 1 · (−1) = −1
Reciprocamente, suponha agora que p > 1 seja um número que satisfaça (p − 1)! ≡ −1 (mod p). Então
todo 1 ≤ a ≤ p − 1 é primo como p, já que a é inversı́vel módulo p: um inverso é dado por −(p − 1)!/a (que
é um inteiro!). Porém isto implica que p é primo: se p = ab para 1 < a, b < p então (a, p) = a 6= 1, o que
contradiz o fato anterior.
Corolário 51. Se p é um primo tal que p ≡ 1 (mod 4) então a equação quadrática
x2 ≡ −1 (mod p)
admite solução.
Demonstração. Basta combinar o teorema de Wilson acima com o truque do complementar. Agrupando a
com −a = p − a para a = 1, 2, . . . , p−1
2 , obtemos
p − 1 2
(p − 1)! ≡ (−1)(p−1)/2 1 · 2 · . . . ·
2
(mod p)
Mas como p ≡ 1 (mod 4), temos que (p − 1)/2 é par. Logo, pelo teorema de Wilson, a equação acima é
equivalente a
p − 1 2
(mod p)
−1 ≡ 1 · 2 · . . . ·
2
e assim podemos tomar x = ±1 · 2 · . . . ·
p−1
2 .
25
Terminamos esta seção com uma importante
Definição 52. O conjunto dos elementos inversı́veis de Z/mZ
def
(Z/mZ)× = {a ∈ Z/mZ | (a, m) = 1}
é chamado de grupo dos elementos inversı́veis de Z/mZ.
−1
Note que o produto de dois elementos inversı́veis a e b é inversı́vel (o seu inverso é a−1 · b
(Z/mZ)× é fechado com relação ao produto.
), assim
Exemplo 53. Temos a seguinte tabela de multiplicação de (Z/15Z)× :
·
1
2
4
7
1 1 2 4 7
2 2 4 8 14
4 4 8 1 13
7 7 14 13 4
8 8 1 2 11
11 11 7 14 2
13 13 11 7 1
14 14 13 11 8

8
11 13 14
8 11 13 14
1 7 11 13
2 14 7 11
11 2 1 8
4 13 14 7
13 1 8 4
14 8 4 2
7 4 2 1
Em Matemática, grupo é o nome emprestado a um conjunto G juntamente com uma operação binária
· (produto) que satisfaz os seguintes três axiomas:
1. (Associatividade) Para quaisquer a, b, c ∈ G, (a · b) · c = a · (b · c)
2. (Existência de elemento neutro) Existe um elemento e ∈ G tal que, para todo a ∈ G, a · e = e · a = a
3. (Existência de inverso) Para qualquer elemento a ∈ G existe um elemento a−1 ∈ G tal que a · a−1 =
a−1 · a = e
Se, além dos três axiomas acima, o grupo G satisfaz
4. (Comutatividade) Para quaisquer a, b ∈ G, a · b = b · a
então G é chamado de grupo abeliano (em homenagem ao matemático norueguês Niels Henrik Abel (1802–
1829)).
2.3
Teorema Fundamental da Aritmética
Vamos agora provar o Teorema Fundamental da Aritmética sobre a fatoração única em primos. Embora
velho conhecido de todos nós desde os tempos do ensino fundamental, os livros escolares não costumam
incluir uma demonstração deste “fato intuitivamente óbvio”. Entretanto este teorema é longe de ser trivial:
basta apenas mencionar que, embora o resultado fosse conhecido dos matemáticos desde os tempos dos
antigos gregos, a primeira demonstração correta foi obtida somente 2000 anos mais tarde por Gauß!
Para mostrar que este teorema é algo especial do conjunto de todos os inteiros Z, façamos um pequeno
experimento mental. Trocando Z pelo conjunto dos pares 2Z, definamos um “primo” em 2Z da mesma
forma que em Z: um inteiro par é “primo” se ele não pode ser escrito como produto de dois pares. Assim,
2, 6, 10, 14, . . . são “primos” enquanto que 4 = 2 · 2, 8 = 2 · 4, 12 = 2 · 6, 16 = 4 · 4, etc. são “compostos” em
2Z. Mas agora
60 = 6 · 10 = 2 · 30
são duas decomposições distintas de 60 em “primos”!
Muito bem, sem maiores delongas, eis o célebre
26
Teorema 54 (Teorema Fundamental da Aritmética). Seja n > 1. Então n pode ser escrito como produto
de potências de primos:
n = pe11 · · · pekk
onde pi denotam primos distintos. Além disso, esta fatoração (dita canônica) é única a menos de uma
permutação dos primos pi .
Demonstração. A demonstração é pelo PIF, sendo que o teorema é claro para n = 2 (base de indução):
sendo 2 primo, ele é a sua própria fatoração canônica, que é única pois em qualquer fatoração de 2 os fatores
primos devem ser menores ou iguais a 2, logo só há uma possibilidade.
Suponha agora que n > 2. Vamos primeiramente mostrar a existência da fatoração. Se n é primo, não
há o que fazer, logo supomos que n é composto, digamos n = ab com 1 < a, b < n. Temos, pela hipótese de
indução, que a e b podem ambos serem escritos como produtos de potências de primos, logo o mesmo vale
para n = ab.
Agora suponha que tenhamos duas fatorações (potencialmente distintas)
n = pe11 · · · pekk = q1f1 · · · qlfl
(∗)
onde pi e qi são primos. Pela alternativa de primo, temos que p1 divide algum dos qi , e renumerando podemos
supor que p1 | q1 . Mas q1 é primo! Assim, a única possibilidade é p1 = q1 , e cancelando um fator p1 = q1
em (∗) obtemos
pe11 −1 · · · pekk = pf11 −1 q2f2 · · · qlfl
Por hipótese de indução, estas duas fatorações são a mesma a menos da permutação de seus fatores. Assim,
podemos supor k = l, pi = qi para todo i, e1 − 1 = f1 − 1 e ei = fi para i ≥ 2. Mas isto implica que as
fatorações (∗) também são iguais, completando a demonstração.
Podemos agora obter alguns “axiomas” vistos na escola:
Corolário 55. Seja
n = pe11 · · · pekk
a fatoração canônica do natural n em primos distintos pi . Temos que os divisores naturais de n são exatamente os números da forma
d = pf11 · · · pfkk
com 0 ≤ fi ≤ ei para todo i. Assim, o número de divisores positivos de n é igual a
(e1 + 1)(e2 + 1) · · · (ek + 1)
Demonstração. Temos que todo d = pf11 · · · pfkk com 0 ≤ fi ≤ ei é um divisor de n pois n/d é inteiro.
Reciprocamente, se n = dt, então escrevendo as fatorações canônicas de d, t e n e comparando os dois lados,
obtemos que os primos que dividem d e t são os mesmos que dividem n e, para um primo fixado pi , os
expoentes fi e gi em d e t devem satisfazer fi + gi = ei , logo 0 ≤ fi , gi ≤ ei . Para mostrar a fórmula do
número de divisores, basta notar que cada fi pode ser escolhido independentemente entre ei + 1 possı́veis
valores 0, 1, . . . , ei .
Corolário 56. Sejam
m = pe11 · · · pekk
n = pf11 · · · pfkk
as fatorações canônicas dos naturais m e n em primos distintos pi com ei , fi ≥ 0 (de modo que podemos
assumir a mesma quantidade de primos nas fatorações acima). Temos
Y min{e ,f }
Y max{e ,f }
i i
i i
mdc(m, n) =
e
mmc(m, n) =
pi
pi
1≤i≤k
1≤i≤k
e portanto
mdc(m, n) · mmc(m, n) = m · n
27
Demonstração. As fórmulas para o mdc e mmc decorrem da descrição dos divisores do corolário anterior,
enquanto que a última fórmula é consequência do fato de que, para todo i, max{ei , fi } + min{ei , fi } =
ei + fi .
A propósito, a última fórmula do corolário anterior fornece um método eficiente para o cálculo do mmc
de dois números: calcule primeiro o mdc via algoritmo de Euclides e depois faça mmc(m, n) = mn/(m, n).
Para números grandes, fatorar em primos é uma operação muito mais custosa do que a que acabamos de
descrever!
Vejamos algumas aplicações dos resultados acima.
√
Exemplo 57. Seja n um inteiro positivo que não é um quadrado perfeito. Então n é um número irracional.
Solução. Seja n = pe11 · · · pekk a fatoração canônica de n em potências de primos pi distintos. Se todos os
ei ’s fossem pares, n seria um
e1 .
√
√ quadrado perfeito, logo existe um ei que é ı́mpar, digamos
A demonstração de que n é irracional é por redução ao absurdo. Suponha que n = ab com a, b inteiros
positivos. Então
a2 = nb2
(∗)
Pelo teorema fundamental da aritmética, a potência de p1 em ambos os lados de (∗) deve ser igual. Se pα
1 é a
2
potência de p1 na fatoração canônica de a, então p2α
será
a
potência
de
p
na
fatoração
canônica
de
a
,
isto
1
1
é, uma potência com expoente par. Analogamente, o expoente da potência de p1 na fatoração canônica de
b2 também é par, digamos 2β, e como a potência de p1 na fatoração de n é pe11 temos que a potência de p1
na fatoração do lado direito de (∗) é 2β + e1 , um número ı́mpar. Logo as potências de p1 do lado esquerdo
e direito de (∗) não podem ser iguais, uma contradição.
Exemplo 58. Se (m, n) = 1 e mn é uma k-ésima potência perfeita, então m e n são ambos k-ésimas
potências perfeitas.
Solução. Temos mn = xk para algum x. Se pt é a potência do primo p na fatoração canônica de x, temos
que pkt é a potência de p na fatoração canônica de mn. Porém, como (m, n) = 1, temos que p ou divide m
ou divide n, mas não ambos; digamos que p | m. Desta forma pkt é a potência de p na fatoração canônica
de m. Como o raciocı́nio anterior é válido para qualquer primo, temos que m e n são ambos produtos de
potências de primos cujos expoentes são múltiplos de k, logo são ambos k-ésimas potências perfeitas.
Observe que se (m, n) 6= 1 a conclusão não é válida! Por exemplo, temos que nem m = 31 e nem
n = 33 são quadrados perfeitos, mas mn = 34 é um quadrado perfeito! Na situação acima, quando
(m, n) = 1, isto não ocorre pois não é possı́vel “quebrar” a potência pkt entre m e n.

O fato anterior é um fato extremamente útil na resolução de equações diofantinas. Veja o
Exemplo 59. Determine todas as soluções de
x2 + y 2 = z 2
com x, y, z inteiros positivos dois a dois primos entre si.
Solução. Note que temos uma fatoração (fatore e fature!)
x2 = z 2 − y 2 = (z − y)(z + y)
Será que (z − y, z + y) = 1? Em caso afirmativo, poderı́amos utilizar o exemplo acima para concluir que
z − y e z + y são ambos quadrados perfeitos. Seja d = (z − y, z + y). Pelo “d divide”, temos que d divide a
soma 2z e a diferença 2y destes dois fatores. Porém, como (z, y) = 1 por hipótese, temos que d | 2. Assim
temos que analisar a paridade destes termos.
28
Como x, y, z são primos entre si, nem todos eles podem ser pares. Logo há exatamente dois ı́mpares e um
par. Por outro lado, analisando módulo 4 como no exemplo 34, temos que não podemos ter x e y ı́mpares
e z par, pois neste caso x2 + y 2 ≡ 2 (mod 4) enquanto que z 2 ≡ 0 (mod 4). Logo z é ı́mpar e por simetria
podemos assumir que x é ı́mpar e y é par. Logo z − y e z + y são ı́mpares e assim d = 1.
Logo pelo exemplo anterior, temos que existem naturais m e n ı́mpares com m < n tais que x = mn,
z − y = m2 e z + y = n2 . Resolvendo o sistema, obtemos
x = mn
y=
n 2 − m2
2
z=
n 2 + m2
2
(†)
Só falta determinar condições para que x, y, z sejam dois a dois primos entre si. Note que qualquer fator
primo comum a dois dentre os inteiros x, y, z deve dividir o terceiro, logo este números serão dois a dois
primos entre si se, e somente se, (y, z) = 1 (por exemplo). Temos (c.f. demonstração do algoritmo de
Euclides)
n 2 − m2 n 2 + m2 n 2 − m2
n 2 + m2 n 2 + m2 =
,
+
,
2
2
2
2
2
2
2
n
+
m
(∗)
=
n2 ,
= n2 , n2 + m2 = (n2 , m2 )
2
(y, z) =
onde (∗) utiliza o fato de que n2 é ı́mpar, de modo que multiplicar a segunda entrada por 2 não altera o mdc.
Assim, (y, z) = 1 ⇐⇒ (m2 , n2 ) = 1 ⇐⇒ (m, n) = 1 (utilize a expressão do mdc em termos da fatoração
de m e n).
Efim, a resposta final é dada por (†) para m > n naturais ı́mpares primos entre si.
Concluı́mos esta seção com uma
Definição 60. Seja p um primo. Dizemos que pα divide exatamente m (em sı́mbolos pα k m) se α é o
expoente de p na fatoração canônica de m (ou, equivalentemetne, se pα é a maior potência de p que divide
m).
Eis uma aplicação clássica:
Teorema 61 (Fatores do Fatorial). Seja p um primo. Sendo
jnk j n k j n k
+ 2 + 3 + ···
α=
p
p
p
temos que pα k n!
Observe que a soma acima é finita pois os temos pni são eventualmente iguais a zero. E relembrando:
para um número real x, ⌊x⌋ denota a parte inteira t de x, isto é, o único inteiro t tal que x − 1 < t ≤ x.
Demonstração. No produto n! = 1 · 2 · . . . · n, apenas os múltiplos de p contribuem com um fator p. Há np
tais múltiplos entre 1 e n. Destes, os que são múltiplos de p2 contribuem com um fator p extra e há pn2
tais fatores. Dentre estes últimos, os que são múltiplos de p3 contribuem com mais um fator p e assim por
diante, resultando na fórmula acima.
Exemplo 62. Determine com quantos zeros termina 100!
Solução. O problema é equivalente a determinar a maior potência de 10 que divide 100! Como há muito
mais fatores 2 do que 5 em 100!, temos que determinar apenas a maior potência de 5 que divide 100! e agora
é só aplicar a fórmula anterior: temos ⌊100/5⌋ + ⌊100/52⌋ = 24, logo a maior potência de 5 que divide 100!
é 524 . Portanto 100! termina em 24 zeros.
29
2.4
Teorema Chinês dos Restos
Vamos agora considerar o problema de resolver sistemas de congruências lineares. Vejamos um
Exemplo 63. Determine o menor inteiro positivo x que deixa restos 1 e 13 nas divisões euclidianas por
109 e 1001, respectivamente.
Solução. Devemos encontrar a menor solução positiva do sistema
(
x ≡ 1 (mod 109)
x ≡ 13 (mod 1001)
Da primeira congruência temos que x = 1 + 109k para algum k ∈ Z. Substituindo na segunda, obtemos
portanto
1 + 109k ≡ 13 (mod 1001) ⇐⇒ 109k ≡ 12 (mod 1001)
(∗)
Agora, multiplicando pelo inverso multiplicativo de 109 módulo 1001, que é igual a 450, temos
(∗) ⇐⇒ 450 · 109k ≡ 450 · 12 (mod 1001) ⇐⇒ k ≡ 395 (mod 1001)
Portanto k = 395 + 1001t e assim
x = 1 + 109 · (395 + 1001t)
⇐⇒
x = 43056 + 109 · 1001t
⇐⇒
x ≡ 43056 (mod 109 · 1001)
e o menor inteiro positivo satisfazendo estas condições é 43056.
Em muitas aplicações, não é necessário obter as soluções explicitamente, apenas saber se elas existem.
Para isto, temos o importante
Teorema 64 (Teorema Chinês dos Restos). Sejam m1 , m2 , . . . , mr inteiros positivos que são primos entre
si, dois a dois, e sejam a1 , a2 , . . . , ar inteiros quaisquer. Então o sistema de conguências
x
x
x
≡ a1
≡ a2
..
.
≡ ar
(mod m1 )
(mod m2 )
(mod mr )
admite uma solução x, única módulo m = m1 m2 . . . mr .
Apresentamos duas demonstrações para este teorema, que ilustram técnicas distintas.
Primeira prova. Considere a função “diagonal”
Z/mZ → Z/m1 Z × · · · × Z/mr Z
a 7→ (a, . . . , a)
Primeiramente, precisamos mostrar que esta função está bem definida, isto é, que escolhendo outro representante de classe b ∈ a em Z/mZ temos b = a em cada Z/mi Z (cuidado, as “barras” denotam redução
módulo diferentes números!) Mas isto decorre facilmente do fato de mi | m, pois b = a + km para algum
k ∈ Z de modo que b ≡ a (mod mi ) para todo i.
O teorema é equivalente a mostrar que esta função é sobrejetora (isto é, que existe um x ∈ Z/mZ que
“atinge” qualquer tupla (a1 , . . . , ar ) ∈ Z/m1 Z × · · · × Z/mr Z. Como o número de elementos em ambos os
30
lados é igual a m = m1 m2 . . . mr , basta mostrar que esta função é injetora. Se dois elementos a, b ∈ Z/mZ
têm mesma imagem, i.e.,
(a, . . . , a) = (b, . . . , b) ⇐⇒ a ≡ b (mod mi ) para todo i
temos que mi | a − b para todo i. Mas como os mi são dois a dois primos entre si, temos (olhando para a
fatoração em primos) que m | a − b, ou seja, a = b em Z/mZ, que era o que querı́amos mostrar.
m
m
, mj = 1 (note que m
é um
Segunda prova. Observe que como (mi , mj ) = 1 para i 6= j, temos que m
j
j
m
m
inteiro!) enquanto que mj ≡ 0 (mod mi ) para i 6= j. Seja bj um inverso multiplicativo de mj módulo mj
m
e mj são primos entre si). Tome
(que existe pois m
j
x=
Módulo mi , temos
x0 ≡
m
b i ai
mi
m
m
b 1 a1 + · · · +
b r ar
m1
mr
(mod mi ) ⇐⇒ x0 ≡ ai
(mod mi )
Então x0 é uma solução do nosso sistema. Agora se x0 e x1 são duas soluções temos x0 ≡ x1 (mod mi ) para
cada i. Como (mi , mj ) = 1 para i 6= j temos como na primeira solução que x0 ≡ x1 (mod m), mostrando a
unicidade.
Exemplo 65. Mostre que existem 1000 inteiros consecutivos compostos.
Solução. Uma maneira de garantir que os inteiros consecutivos x + 1, x + 2, . . . , x + 1000 sejam compostos é
torná-los múltiplos de primos fixos, com o cuidado de escolher x grande o suficiente para que nenhum destes
números coincida com um destes primos.
Assim, escolha 1000 primos distintos p1 , . . . , p1000 e considere o sistema
x
x
≡ −1 (mod p1 )
≡ −2 (mod p2 )
..
.
x
≡ −1000 (mod p1000 )
Pelo Teorema Chinês dos Restos, o sistema acima possui infinitas soluções, logo basta tomar uma solução x
suficientemente grande.
2.5
2.5.1
Exercı́cios
Básicos
24. Resolva as seguintes equações diofantinas lineares:
(a) 172x + 13y = 1
(c) 123x + 130y = 13
(e) 391x + 1377y = 34
(b) 233x + 144y = 1
(d) 280x + 49y = 2
(f ) 22x + 121y = −11
25. Mostre que se x e y são tais que N = (x + 6y)(2x + 5y)(3x + 4y) é divisı́vel por 7 então N é múltiplo
de 343.
26. Encontre o inverso multiplicativo (ou mostre que ele não existe):
(a) 7 mod 13
(b) 12 mod 143
(c) 22 mod 121
(d) 19 mod 200
31
27. Com quantos zeros termina 2008! quando escrito na notação decimal?
28. Prove o seguinte critério de divisibilidade por 7: dado um inteiro n, seja d o último dı́gito de n e m o
número obtido a partir de n apagando-se o último dı́gito d; então n é divisı́vel por 7 se, e somente se, m − 2d
é divisı́vel por 7. Por exemplo, para n = 8638, temos 863 − 2 · 8 = 847 e 84 − 2 · 7 = 70, que é divisı́vel por
7, logo 8638 é divisı́vel por 7 também.
29. Sejam m0 , m1 , . . . , mr inteiros positivos que são dois a dois primos entre si. Mostre que existem r + 1
inteiros consecutivos s, s + 1, . . . , s + r tal que mi | s + i para i = 0, 1, . . . , r.
30. Existem 2009 inteiros consecutivos tal que cada é divisı́vel por uma centésima potência de um primo?
2.5.2
Lição de Casa
31. (Estônia) Determine todos os restos possı́veis da divisão do quadrado de um número primo com 120 por
120.
32. Seja n um número natural e seja
n = pe11 · · · pekk
a fatoração canônica de n em potências de primos pi distintos. Mostre que a soma dos divisores positivos
de n é igual a
pek +1 − 1
pe11 +1 − 1 pe22 +1 − 1
·
· ...· k
p1 − 1
p2 − 1
pk − 1
2.5.3
Questões de Prova
33. Um ponto inteiro (x, y) ∈ Z2 é visı́vel se (x, y) = 1. Existe um ponto (a, b) ∈ Z2 cuja distância a todo
ponto visı́vel é pelo menos 1000?
34. (IMO) Encontre um par de inteiros positivos a e b tais que
(i) ab(a + b) não é divisı́vel por 7;
(ii) (a + b)7 − a7 − b7 é divisı́vel por 77 .
35. Seja p(x) um polinômio não constante com coeficientes inteiros e seja k um inteiro qualquer. Prove que
existe um inteiro m tal que p(m) tem pelo menos k fatores primos distintos.
32
Capı́tulo 3
Teorema de Euler-Fermat
Conforme vimos, para calcular uma potência ad mod m, é interessante obter algum expoente n tal que
an ≡ ±1 (mod m) (nossa velha filosofia ≡ ♥ ± 1 lembra-se?). O teorema de Euler-Fermat mostra como
encontrar este “expoente mágico” n > 0 de modo que an ≡ 1 (mod m).
Primeiramente, vejamos os casos em que podemos esperar a existência de tal “expoente mágico”. Se
d = (a, m) 6= 1, tal expoente não pode existir, pois caso contrário terı́amos
an ≡ 1 (mod m) ⇐⇒ an = mx + 1 para algum x
Porém, d divide a e m, logo d divide 1 = an − mx, uma contradição.
No caso em que a e m são primos entre si, aı́ sim podemos esperar encontrar tal “expoente mágico”. De
fato, em Z/mZ considere as potências de a
1, a, a2 , a3 , a4 , . . .
Como Z/mZ é um conjunto finito, esta lista contém (muitos) elementos repetidos. Se i > j são tais que
ai = aj , como a e m são primos entre si, temos que a é inversı́vel em Z/mZ (ou seja, a ∈ (Z/mZ)× ) e desta
forma
ai = aj ⇐⇒ ai−j = 1 ⇐⇒ ai−j ≡ 1 (mod m)
o que mostra a existência do “expoente mágico” n = i − j > 0.
Melhor do que saber que ele existe, é saber calculá-lo. É para isto que temos o teorema de Euler-Fermat.
3.1
Função φ de Euler
Definição 66. Seja n um inteiro positivo. A função φ de Euler é definida como
φ(m)
def
=
=
quantidade de inteiros 1 ≤ d ≤ m tais que d e m são primos entre si
número de elementos do grupo (Z/mZ)×
A função φ de Euler foi introduzida, advinhem, pelo grande matemático suı́ço Leonhard Paul Euler
(1707–1783), em conexão com o teorema de Euler-Fermat que discutiremos a seguir. Esta função também
é conhecida em Inglês por “Euler ‘totient’ function”, nome dado por James Joseph Sylvester (1814–1897),
matemático britâncio que adorava inventar novas palavras complicadas.
Exemplo 67. Eis alguns exemplos:
• φ(1) = 1;
33
• φ(12) = 4 pois (Z/12Z)× = {1, 3, 5, 7} tem 4 elementos;
• temos que
p é um número primo ⇐⇒ φ(p) = p − 1
De fato, se p é primo, então dentre os números 1, 2, . . . , p, todos são primos com p com exceção do
próprio p. Por outro lado, se p = ab é composto com 1 < a, b < p, então na lista 1, 2, . . . , p, os números
a, b e p não são primos com p, logo φ(p) < p − 1 neste caso. Finalmente, se p não é primo e nem
composto (então o que ele é?), temos que p = 1 (ah, é verdade, 1 não é nem primo nem composto!)
logo φ(p) = 1 6= p − 1 = 0.
Calcular φ diretamente através da definição pode não ser muito prático, então vamos provar
Lema 68 (Calculando φ). Seja
αk
α2
1
m = pα
1 · p2 · . . . · pk
a fatoração canônica de m em potências de primos distintos pi . Então
φ(m)
=
=
αk −1
α1 −1
1
2 −1
k
(pα
) · (pα2 − pα
) · . . . · (pα
)
1 − p1
2
k − pk
2
1
1
1
· 1−
· ...· 1−
m· 1−
p1
p2
pk
Demonstração. Seja
Q
def
=
=
probabilidade de que um número 1 ≤ d ≤ m seja primo com m
φ(m)
m
Vamos calcular esta probabilidade de outra maneira. Temos que d é primo com m se, e somente se, d não é
múltiplo de nenhum fator primo pi que divide m. A probabilidade de que d seja múltiplo de pi é p1i já que há
pi possı́veis restos igualmente prováveis para d mod pi . Assim, a probabilidade de que d não seja múltiplo
de pi é 1 − p1i . Portanto a probabilidade Q de que d não seja múltiplo de nenhum pi é
1
1
1
Q= 1−
· 1−
· ...· 1 −
p1
p2
pk
Comparando as duas fórmulas para Q, obtemos o resultado.
Exemplo 69. Pela fórmula temos
1
1
φ(12) = 12 1 −
1−
=4
2
3
que, incrivelmente, coincide com o valor que encotramos anteriormente!
Utilizando a fórmula acima, é fácil provar o corolário a seguir, que deixamos como exercı́cio para você:
Corolário 70. A função φ é multiplicativa, isto é, para (m, n) = 1 temos
φ(m · n) = φ(m) · φ(n)

Esta relação só vale quando m e n são primos entre si!
3.2
Teorema de Euler-Fermat
Agora estamos prontos para o teorema propriamente dito! Começamos enunciando o teorema e suas variantes.
Em seguida, esboçamos a sua prova num caso particular, mas que já encerra todos os ingredientes principais
da demonstração no caso geral, que é atacado logo em seguida.
34
3.2.1
Enunciado do teorema e suas variantes
Teorema 71 (Euler-Fermat). Se (a, m) = 1, então
aφ(m) ≡ 1
Equivalentemente, se a ∈ (Z/mZ)× então
(mod m)
aφ(m) = 1
Trocando em miúdos: se a base a é prima com o módulo m, então existe um expoente, a saber φ(m), tal
que aφ(m) ≡ 1 (mod m). Note que uma vez encontrado um tal “expoente mágico”, há infinitos deles: para
qualquer k ≥ 0 temos automaticamente
ak·φ(m) ≡ 1 (mod m)
Exemplo 72. (Para os céticos) Tome a = 3 e m = 14. Temos φ(14) = 6. Fazendo as contas “na raça”:
33 ≡ −1 (mod 14) =⇒ 36 ≡ 1 (mod 14)
Incrı́vel! Não é que funciona mesmo. . .
O teorema, no formato acima, foi demonstrado por Euler em 1736. Um caso particular já havia sido
(de)monstrado pelo grande matemático francês Pierre de Fermat (1601–1665) quase um século antes, a saber
o caso em que m = p é um primo. Neste caso, temos φ(p) = p − 1, logo
ap−1 ≡ 1
(mod p)
para todo a primo com p (isto é só um jeito complicado de dizer que a não é um múltiplo de p). Agora
vamos multiplicar ambos os membros da congruência por a. Temos
ap ≡ a
(mod p)
(∗)
Pensemos mais um pouco. Temos que (∗) só poderia “falhar” se a não fosse primo com p, isto é, só se
p | a, o que na linguagem das congruências é o mesmo que a ≡ 0 (mod p). Ora, substituindo este valor em
(∗), obtemos uma relação verdadeira ainda. Assim (∗) vale para todo inteiro a. Obtemos como corolário o
resultado original de Fermat:
Teorema 73 (Pequeno Teorema de Fermat). Seja p um primo. Então para todo inteiro a temos
ap ≡ a
(mod p)
O teorema acima admite uma prova combinatória bem simples e interessante. Suponha que desejamos
formar colares com p contas e temos contas de a cores distintas. De quantas maneiras podemos montar estes
colares, sendo que dois colares são considerados o “mesmo” se um pode ser obtido a partir do outro por meio
de uma rotação?
Se não houvesse rotações envolvidas, a resposta seria apenas o número de sequências (a1 , a2 , . . . , ap )
onde ai representam uma dentre a cores, ou seja, o número de colares seria ap . Com as rotações, cada colar
“distinto” pode corresponder a mais de uma sequência (a1 , a2 , . . . , ap ) diferente. Temos dois casos a analisar:
• Todas as contas têm a mesma cor. Neste caso há a colares.
• O colar não é monocromático. Neste caso, cada colar dá origem, por rotação, a exatamente p sequências
(a1 , a2 , . . . , ap )
(a2 , a3 , . . . , ap , a1 )
(a3 , a4 , . . . , ap , a1 , a2 )
..
.
(ap , a1 , a2 , . . . , ap−1 )
35
De fato, vamos mostrar que se duas das sequências acima são iguais então o colar é monocromático.
Suponha por exemplo que (a1 , a2 , . . . , ap ) = (ai+1 , ai+2 , . . . , ai+p ) para algum 0 < i < p (onde os
ı́ndices são tomados “módulo p”), isto é, a sequência (a1 , a2 , . . . , ap ) é igual ao seu i-ésimo “shift”.
Então terı́amos
shift
shift
shift
shift
shift
a1 = ai+1 = a2i+1 = a3i+1 = a4i+1 = · · ·
(onde novamente os ı́ndices são tomados “módulo p”). Note que basta mostrar que os números 1, i +
1, 2i + 1, 3i + 1, . . . , (p − 1)i + 1 percorrem todos os inteiros módulo p (ou seja, que eles formam um
sistema completo de resı́duos módulo p pela definição 35). Se houvesse uma repetição ri + 1 ≡ si + 1
(mod p), como i é inversı́vel módulo p (0 < i < p), terı́amos r ≡ s (mod p). Mas como 0 ≤ r, s < p,
isto implica r = s, ou seja, a repetição ocorreu porque começamos como o mesmo elemento! Logo os
p números 1, i + 1, 2i + 1, 3i + 1, . . . , (p − 1)i + 1 realmente formam um sistema completo de restos,
terminando a prova.
O total de colares é portanto a soma dos monocromáticos e dos “policromáticos”, isto é,
a+
ap − a
p
p
Mas este total é um número inteiro (afinal de contas, estamos contando número de colares)! Logo a p−a é
um número inteiro, isto é, ap ≡ a (mod p), “and that’s Fermat for you!”
O teorema de Fermat tem uma consequência fantástica, o sonho de todo aluno que estuda aritmética na
escola!
Corolário 74 (O sonho de todo estudante). Se p é um primo então
(a + b)p ≡ ap + bp
(mod p)
para quaisquer inteiros a e b.
Demonstração. De fato, aplicando o pequeno teorema de Fermat três vezes temos

p

(a + b) ≡ a + b (mod p)
p
a ≡ a (mod p)

 p
b ≡ b (mod p)
Assim, módulo p, (a + b)p ≡ a + b ≡ ap + bp .
3.2.2
Um esboço da demonstração
Vamos ver um caso particular: façamos a = 3 e m = 14. Vamos mostrar que 3φ(14) ≡ 1 (mod 14). Bom,
precisamos conhecer φ(14). Para isso, listemos os números positivos menores que 14 e primos com 14:
1
3 5
9
11 13
Vamos agora multiplicar todos estes números por a = 3 e calcular cada um deles módulo 14:
1·3
3·3
5·3
9·3
11 · 3
13 · 3
≡ 3
≡ 9
≡ 1
≡ 13
≡ 5
≡ 11
36
(mod
(mod
(mod
(mod
(mod
(mod
14)
14)
14)
14)
14)
14)
Vejam! Todos os números positivos menores que 14 e primos com 14 apareceram novamente, só que em
outra ordem! Multiplicando todas estas φ(14) congruências, temos
(1 · 3 · 5 · 9 · 11 · 13) · 3φ(14) ≡ (3 · 9 · 1 · 13 · 15 · 11) (mod 14)
Como 1 · 3 · 5 · 9 · 11 · 13 é primo com 14 (estamos multiplicando números sem fatores em comum com 14,
logo o produto continua sem fatores em comum com 14), este produto é inversı́vel módulo 14 e portanto
cancelando obtemos
3φ(14) ≡ 1 (mod 14)
Lembra algo? Se você disse “Euler-Fermat”, acertou!
3.2.3
No caso geral. . .
O que fizemos? Primeiro, listamos os números positivos a1 , a2 , . . . , aφ(m) menores que m e primos com
m. Aı́ multiplicamos cada um deles por a e, calculando tudo módulo m, obtivemos os mesmo números
a1 , a2 , . . . , aφ(m) em outra ordem. Depois era só multiplicar tudo.
Será que este fenômeno é uma mera coincidência? Obra do acaso? Ou seria consequência do
Teorema 75 (“Gira-Gira”). Seja a primo com m. Multiplicação por a permuta os elementos de (Z/mZ)×
e de Z/mZ. Explicitamente: se
T = {a1 , a2 , . . . , aφ(m) }
é o conjunto dos números positivos menores ou iguais a m e primos com m (de modo que “T mod m =
(Z/mZ)× ”), então
T = {a · a1 mod m, a · a2 mod m, . . . , a · aφ(m) mod m}
Se
S = {b1 , b2 , . . . , bm }
é um sistema completo de resı́duos módulo m (de modo que “S mod m = Z/mZ”) então
{a · b1 , a · b2 , . . . , a · bm }
também é um sistema completo de resı́duos módulo m.
Demonstração. Vamos demonstrar que multiplicação por a permuta os elementos de (Z/mZ)× e deixamos
o outro caso para o leitor.
Sejam
a1 , a2 , . . . , aφ(m)
os φ(m) elementos de (Z/mZ)× . Temos que
a · a1 , a · a2 , . . . , a · aφ(m)
também são elementos de (Z/mZ)× pois a ∈ (Z/mZ)× por hipótese e (Z/mZ)× é fechado por multiplicação.
Para mostrar que esta lista contém todos os elementos de (Z/mZ)× (em alguma ordem), basta mostrar que
eles são todos distintos, já que há φ(m) deles.
Mas isto é fácil: se houvesse uma repetição a · ai = a · aj para dois elementos distintos ai e aj , cancelando
a obterı́amos ai = aj , um absurdo.
Vamos agora concluir a demonstração do teorema de Euler-Fermat. Com a notação acima, pelo “giragira”, temos que
a · a1
a · a2
≡
≡
..
.
a′1
a′2
a · aφ(m)
≡
a′φ(m)
37
(mod m)
(mod m)
(mod m)
onde os a′i são uma permutação dos ai . Assim, multiplicando estas equações, obtemos
Y
Y
ai (mod m)
ai ≡
aφ(m)
1≤i≤φ(m)
1≤i≤φ(m)
Q
Como cada ai é inversı́vel módulo m, o produto 1≤i≤φ(m) ai também é inversı́vel módulo m. Pelo cancelamento, temos que aφ(m) ≡ 1 (mod m), como desejado.
3.3
Utilizando o teorema de Euler-Fermat
Mostraremos aqui algumas aplicações do teorema de Euler-Fermat. A primeira é facilitar nossas contas.
Exemplo 76. Calcule o resto da divisão de 22001 por 101.
Solução. Temos que 2 e 101 são primos entre si. Utilizando o teorema de Euler-Fermat, temos φ(101) = 100
e portanto, como 2001 = 100 · 20 + 1,
22001 = 2100
20
· 2 ≡ 120 · 2
(mod 101) =⇒ 22001 ≡ 2
(mod 101)
Observe que podemos pensar isto da seguinte forma: como 2001 ≡ 1 (mod φ(101)), temos 22001 ≡ 21
(mod 101). Ou seja, as potências de 2 módulo 101 são “periódicas módulo φ(101)”.
Eis uma aplicação não exatamente do teorema de Euler-Fermat mas sim do “gira-gira”:
Exemplo 77. Mostre que
S = 16 + 26 + 36 + 46 + · · · + 1006
é divisı́vel por 101.
Solução. Multiplicando S por 26 temos
26 S = (2 · 1)6 + (2 · 2)6 + · · · + (2 · 100)6
Pelo gira-gira, temos que {2 · 1, 2 · 2, . . . , 2 · 100} = {1, 2, . . . , 100}, assim
26 S ≡ 16 + 26 + 36 + 46 + · · · + 1006
(mod 101)
⇐⇒
⇐⇒
⇐⇒
26 S ≡ S
(mod 101)
(26 − 1)S ≡ 0 (mod 101)
S ≡ 0 (mod 101)
já que 26 − 1 = 63 é primo com 101.
Outra aplicação usa simplesmente a existência do “expoente mágico” φ(m).
Exemplo 78. Mostre que existe uma potência de 3 cuja representação decimal contém pelo menos 1000
zeros sucessivos.
Demonstração. Como (3, 101001 ) = 1, podemos escrever
1001
3φ(10
1001
Assim, os últimos 1001 dı́gitos de 3φ(10
)
)
≡1
(mod 101001 )
são 0000 . . . 1 (1000 zeros), o que termina o problema.
Exemplo 79. Mostre que existem infinitos números da forma 200 . . . 01 que são múltiplos de 2001.
38
Solução. Seja n o número de zeros em 200 . . . 01. Temos 200 . . . 01 = 2 · 100 . . . 00 + 1 = 2 · 10n+1 + 1. Assim,
basta encontrarmos infinitos valores de n > 2 para os quais 2 · 10n+1 + 1 ≡ 0 (mod 2001). Mas
2 · 10n+1 + 1 ≡ 0 (mod 2001)
2 · 10n+1 + 1 ≡ 2001 (mod 2001)
⇐⇒
2 · 10n+1 ≡ 2000 (mod 2001)
⇐⇒
10n+1 ≡ 103
⇐⇒
(mod 2001)
Como n + 1 > 3, temos então que encontrar infinitos n’s tais que
10n−2 ≡ 1
(mod 2001)
(∗)
Observe que a expressão acima é parecida com a do teorema de Euler-Fermat. De fato, como (10, 2001) =
1, temos, pelo teorema de Euler-Fermat, que existe um expoente φ(2001) tal que
10φ(2001) ≡ 1
(mod 2001)
Mas a partir de um expoente, é fácil encontrar infinitos: elevando a congruência anterior a um número
positivo k, temos
10φ(2001)k ≡ 1 (mod 2001)
(∗∗)
Assim, tomando n − 2 = φ(2001)k ⇐⇒ n = φ(2001)k + 2, temos, a partir de (∗∗), o que queremos
em (∗). Assim, existem infinitos números da forma 200 . . . 01 (aqueles com n = φ(2001)k + 2 zeros) que são
múltiplos de 2001.
O próximo problema mostra como o teorema de Euler-Fermat é útil para reconhecer quando não há
soluções para certas equações módulo m.
Exemplo 80. Mostre que se m e n são inteiros tais que 103 divide m2 + n2 então 103 divide m e n.
Solução. Suponha por absurdo que n 6= 0. Então m 6= 0 também: caso contrário, como m2 + n2 ≡ 0
(mod 103), terı́amos que m ≡ 0 (mod 103) =⇒ n2 ≡ 0 (mod 103) ⇐⇒ 103 | n2 ⇐⇒ 103 | n ⇐⇒ n ≡ 0
(mod 103) onde a equivalência 103 | n2 ⇐⇒ 103 | n é válida pois 103 é primo.
Como n 6= 0 e 103 é primo, temos que n é inversı́vel em Z/103Z. Multiplicando a hipótese inicial
m2 + n2 = 0 por (n−1 )2 obtemos
m2 + n2 = 0 =⇒ (m · n−1 )2 + 1 = 0 ⇐⇒ (m · n−1 )2 = −1,
isto é, −1 é um “quadrado perfeito módulo 103”. Mas isto é impossı́vel: elevando ambos os lados a (103 −
1)/2 = 51, obtemos
(m · n−1 )2 = −1 =⇒ (m · n−1 )102 = −1
o que contradiz o teorema de Euler-Fermat (m · n−1 )102 = 1 (como m 6= 0, temos m · n−1 6= 0, logo podemos
aplicar o teorema; por outro lado 1 6≡ −1 (mod 103)).
O próximo exemplo ilustra a utilização do binômio de Newton juntamente com o teorema de EulerFermat.
Exemplo 81. Dizemos que um número natural n tem a propriedade P se, e somente se,
n | an − 1 =⇒ n2 | an − 1
para a ∈ Z.
(a) Mostre que todo número primo possui a propriedade P .
(b) Mostre que existem infinitos números compostos que possuem a propriedade P .
39
Solução. Podemos escrever a propriedade P como
an ≡ 1 (mod n) =⇒ an ≡ 1
(mod n2 )
(a) Suponha que n seja primo. Temos an ≡ a (mod n) pelo pequeno teorema de Fermat, logo
an ≡ 1 (mod n) =⇒ a ≡ 1 (mod n) ⇐⇒ a = kn + 1 para algum k inteiro
Devemos mostrar que (kn + 1)n ≡ 1 (mod n2 ) para n primo. Pela fórmula do binômio de Newton,
(kn + 1)n =
n X
n
n
n
n
(kn)i 1n−i =
(kn)n + · · · +
(kn)2 +
kn + 1
i
n
2
1
i=0
Tomando (kn + 1)n mod n2 , temos que todos as parcelas da forma ni (kn)i para i ≥ 2 são divisı́veis por
n2 . Logo
n
(kn + 1)n ≡
(kn) + 1 = n · kn + 1 ≡ 1 (mod n2 ),
1
que é o que querı́amos demonstrar.
(b) Vamos encontrar infinitos números compostos que possuem a propriedade P . Os números primos parecem
ser ótimos exemplos, então podemos tentar n = 2p onde p é primo ı́mpar.
Novamente pelo pequeno teorema de Fermat ap ≡ a (mod p) e desta forma a2p ≡ a2 (mod p). Portanto
an ≡ 1
(mod n)
⇐⇒
⇐⇒
a2p ≡ 1 (mod 2p) ⇐⇒ a2 ≡ 1 (mod p)
a2 = kp + 1 para algum k inteiro
Além disso, como n é par, de an ≡ 1 (mod n) temos também que a deve ser ı́mpar.
Vamos mostrar agora que n = 2p tem a propriedade P . Devemos mostrar que a2p = (kp + 1)p ≡ 1
(mod 4p2 ) para p > 2 primo. Isso é o mesmo que mostrar que: (i) (kp + 1)p ≡ 1 (mod 4); e (ii) (kp + 1)p ≡ 1
(mod p2 ).
2
Já demonstramos (ii) no item (a). Mostremos (i). Lembrando que (kp+1)p = a2p = (ap ) e que a é ı́mpar
p
p
2p
(e consequentemente a também), temos a = 2ℓ + 1 para algum ℓ inteiro e assim a = 4ℓ2 + 4ℓ + 1 ≡ 1
(mod 4), o que completa nossa demonstração.
3.4
3.4.1
Exercı́cios
Básicos
36. Mostre que 22225555 + 55552222 é divisı́vel por 7.
37. Calcule os dois últimos dı́gitos de 72001 .
38. Mostre que
S = 148 + 248 + 348 + · · · + 9648
é divisı́vel por 97.
39. Mostre que existem infinitos números da forma 19999 . . . 9991 que são múltiplos de 1991.
40. Mostre que se m e n são inteiros tais que 1999 divide m2 + n2 então 1999 divide m e n.
40
3.4.2
Lição de casa
41. Mostre que
(a) não existe x inteiro tal que 43 | x2 + 1
(b) não existe x inteiro tal que 103 | x3 − 2
(c) se 43 | x2 + y 2 então 43 | x e 43 | y
(d) se 103 | x3 − 2y 3 então 103 | x e 103 | y
42.
(a) Mostre que se p = 4k + 3 (k ∈ Z) é primo e m e n são inteiros tais que p divide m2 + n2 , então p
divide m e n.
(b) Mostre que se t = m2 + n2 pode ser escrito como soma de dois quadrados perfeitos, então todos os
fatores primos da forma 4k + 3, k inteiro, devem aparecer na fatoração de t com expoente par.
43. Mostre que para todo inteiro positivo n existe
(a) uma potência de 7 cuja representação decimal contém pelo menos n zeros sucessivos.
(b) uma potência de 2 cuja representação decimal contém pelo menos n zeros sucessivos.
Dica: no item (b), aplique o teorema de Euler-Fermat para a = 2 módulo 5k .
44. Seja p um primo.
(a) Mostre que para 0 < k < p o coeficiente binomial
p
k
é divisı́vel por p.
(b) Utilize o item anterior e o binômio de Newton para provar, por indução em a, que ap ≡ a (mod p)
(pequeno Teorema de Fermat) para todo natural a.
45. Mostre que existem infinitos números da forma 100000 . . . 0001 que são divisı́veisl por 49.
3.4.3
Questões de Provas
46. (IMO) Sejam a e b inteiros positivos tais que 15a+ 16b e 16a− 15b sejam quadrados perfeitos. Encontrar
o menor valor que pode assumir o menor destes quadrados.
Dica: considere (15a + 16b)2 + (16a − 15b)2 e analise módulo um número conveniente.
47. Um número inteiro positivo é denominado número duplo se sua representação decimal consiste de um
bloco de dı́gitos não iniciado por zero seguido imediatamente de um bloco idêntico. Por exemplo, 360360 é um
número duplo, mas 36036 não é. Mostre que existem infinitos números duplos que são quadrados perfeitos.
Dica: tente encontrar números duplos com 6, 8 ou 10 dı́gitos!
48. Prove que o conjunto {2k − 3 | k ∈ N} contém um subconjunto infinito cujos membros são primos dois
a dois.
41
Capı́tulo 4
Ordem e Raı́zes Primitivas
Neste capı́tulo, estudaremos propriedades relacionadas ao grupo (Z/mZ)× . O conceito fundamental é o de
ordem de um inteiro a módulo m, que é uma espécie de “perı́odo” para as potências de a módulo m. Em
seguida, estudaremos os inteiros a que possuem “perı́odo máximo” φ(m), as chamadas raı́zes primitivas.
4.1
Ordem e menor divide
Definição 82. Sejam a e m inteiros primos entre si. A ordem de a módulo m (ou de a ∈ (Z/mZ)× ),
denotada por ordm a, é o menor inteiro d > 0 tal que
ad ≡ 1 (mod m) ⇐⇒ ad = 1
A ordem d = ordm a é uma espécie de “perı́odo” para as potências de a módulo m, pois como ad = 1,
temos que ai+d = ai e assim as potências ai , i = 0, 1, 2, . . . se repetem de d em d. Este perı́odo é o “perı́odo
mı́nimo” pois tomamos d o menor possı́vel.
Exemplo 83. Para 2 ∈ Z/31Z, temos
0
2
1
2
2
2
3
2
4
2
= 1
= 2
= 4
= 8
= 16
5
2
6
2
7
2
8
2
9
2
=
=
=
=
=
1
2
4
8
16
...
de modo que ord31 2 = 5.
Assim como o perı́odo mı́nimo de uma função trigonométrica divide qualquer outro perı́odo desta função,
temos aqui também o
Teorema 84 (“Menor divide”). Se at ≡ 1 (mod m) então ordm a | t. Em particular, ordm a divide φ(m).
Demonstração. Seja d = ordm a e t = d · q + r a divisão euclidiana de t por d, onde 0 ≤ r < d. Assim, como
ad ≡ 1 (mod m), temos
q
at ≡ 1 (mod m) ⇐⇒ ad · ar ≡ 1 (mod m) ⇐⇒ ar ≡ 1 (mod m)
Se r > 0, temos um expoente menor que d tal que ar ≡ 1 (mod m), absurdo. Logo r = 0 e portanto d divide
t. Por outro lado, como aφ(m) ≡ 1 (mod m) por Euler-Fermat, devemos ter d | φ(m) pelo que acabamos de
demonstrar.
42
Podemos utilizar o “menor divide” para facilitar o cálculo da ordem, evitando ter que listar todas as
potências.
Exemplo 85. Determine ord100 3.
Solução. Para otimizar as contas, vamos “quebrar” o módulo 100 em potências de primos. Note que
3φ(25) ≡ 1 (mod 25) e 3φ(4) ≡ 1 (mod 4). Temos φ(25) = 20 e φ(4) = 2, portanto temos que 320 ≡ 1
(mod 25) e 320 ≡ 1 (mod 4). Como 4 e 25 são primos entre si e 320 − 1 é divisı́vel tanto por 4 como por 25,
temos que 320 ≡ 1 (mod 100), logo ord100 3 | 20 pelo “menor divide”.
Para mostrar que ord100 3 = 20, basta testar os divisores “maximais” de 20, que são 20/2 = 10 e 20/5 = 4
(qualquer divisor próprio de 20 divide um dos dois números). Fazendo as contas, temos que 310 ≡ 49
(mod 100) e 34 ≡ 81 (mod 100). Se ord100 3 fosse algum divisor próprio de 20, uma destas congruências
deveria ser igual a 1 módulo 100, o que não ocorre. Logo ord100 3 = 20.
O conceito de ordem aparece em diversos problemas em Teoria dos Números. Vejamos dois exemplos
tı́picos.
Exemplo 86. Sejam a e n dois inteiros positivos primos entre si. Mostre que n | φ(an − 1).
Solução. Note que n é o menor inteiro positivo tal que an ≡ 1 (mod an − 1). Assim, n é a ordem de a
módulo an − 1 e o resultado segue diretamente do “menor divide”.
Exemplo 87. Mostre que se n é um inteiro maior que 1, então n não divide 2n − 1.
Demonstração. Suponhamos por absurdo que exista um valor de n > 1 tal que n divide 2n − 1. Seja p o
menor primo que divide n. Temos que, como n divide 2n − 1, então p divide 2n − 1, isto é, 2n ≡ 1 (mod p).
Seja d = ordp 2.
Como φ(p) = p − 1, temos pelo “menor divide” que

d
(

≡ 1 (mod p)
2
d|p−1
2p−1 ≡ 1 (mod p) =⇒

d
|n
 n
2
≡ 1 (mod p)
Logo d é divisor comum de p − 1 e n e portanto divide (p − 1, n). Mas todos os divisores primos de p − 1 são
menores que p e portanto não aparecem na fatoração de n pela minimalidade de p. Logo (p − 1, n) = 1 e o
único valor possı́vel para d é 1.
Logo 21 ≡ 1 (mod p) ⇐⇒ p | 1, absurdo. Assim, não existe n > 1 tal que n divide 2n − 1.
4.2
Lema de Hensel
O lema de Hensel é um resultado que nos permite calcular a potência exata de um primo que divide um certo
número. O lema em si é apenas uma simples aplicação do binômio de Newton, mas ele é uma ferramenta
muito útil na resolução de equações diofantinas, especialmente as que envolvem variáveis no expoente.
Relembrando: para um primo p, escrevemos pα k m se pα é a maior potência de p que divide m (ver
definição 60).
Teorema 88 (Lema de Hensel). Seja p um primo ı́mpar, a um inteiro e n um inteiro positivo. Sejam α e
β inteiros não negativos, com α > 0.
(i) Se pβ k n e pα k a − 1 então pα+β k an − 1 (atenção, p deve dividir a − 1 pois α > 0! Mas note que p
não precisa dividir n)
(ii) Se n é ı́mpar, pβ k n e pα k a + 1 então pα+β k an + 1 (mesma resalva do item (i)).
43
Demonstração. Vamos demonstrar o item (i) e deixar o item (ii) como exercı́cio. Observe que n = pβ · k,
sendo que k não é múltiplo de p. Primeiro provaremos o resultado para k = 1, ou seja, n = pβ .
A demonstração é por indução sobre β. Para β = 0 o resultado é óbvio. Suponha que o resultado é
t
t
válido para β = t, ou seja, que ap − 1 = pα+t · m, com m não divisı́vel por p. Assim, ap = pα+t · m + 1.
Elevando os dois lados a p e utilizando binômio de Newton, obtemos
t+1
ap
= (pα+t · m + 1)p
p p
p p−1 α+t
p p−2
p
α+t
2
=
1 +
1
·p m+
1
· (p m) + · · · +
(pα+t m)p
0
1
2
p
t+1
⇐⇒ ap
− 1 = pα+t+1 (m + p · v),
em que v é um inteiro. Logo, como m não é divisı́vel por p, temos que m + p · v também não é múltiplo de
p, o que conclui a demonstração para o caso especial k = 1.
Se k > 1, basta observar que
β
ap
β
·k
− 1 = ap
β
k
β
β
− 1 = (ap − 1) · (ap
·(k−1)
β
+ ap
·(k−2)
β
+ · · · + ap + 1)
(∗)
Como ap ≡ 1 (mod p) (pois p | a − 1 por hipótese) temos que
β
ap
·(k−1)
β
+ ap
·(k−2)
β
+ · · · + ap + 1 ≡ 1 + 1 + · · · + 1 ≡ k
{z
}
|
(mod p)
k uns
e como k 6≡ 0 (mod p), temos que o segundo fator em (∗) não é divisı́vel por p. Logo apenas o primeiro fator
em (∗) contribui com fatores p e pelo caso especial já provado temos que pα+β k an − 1.
Exemplo 89. Encontre todos os inteiros não negativos x e y tais que
7y − 2 · 3x = 1
Demonstração. Temos 2 · 3x = 7y − 1. Note que a maior potência de 3 que divide 7 − 1 é 3. Seja 3m a maior
potência de 3 que divide y. Então, pelo lema de Hensel, a maior potência de 3 que divide 7y − 1 é 3m+1 .
Logo x = m + 1.
Agora vamos utilizar desigualdades. Como 3m divide y, 3m ≤ y, e assim
m
2 · 3m+1 = 2 · 3x = 7y − 1 ≥ 73 − 1.
o que impõe uma forte restrição sobre os possı́veis valores de m, pois para m suficientemente grande o lado
da direita é muito maior que o da esquerda, mas a desigualdade está no sentido oposto!
Sendo t = 3m , temos 6t ≥ 7t − 1 ⇐⇒ 7t ≤ 1 + 6t,
que é verdadeiro para t = 0 e t = 1 mas falso
para t > 1, pois nesse caso 7t = (6 + 1)t > 0t 1t + 1t 1t−1 · 6 = 1 + 6t. Assim, a única possibilidade é
t = 1 ⇐⇒ m = 0, logo x = m + 1 = 1 e assim y = 1.
4.3
Raı́zes Primitivas
Já sabemos que ordm a | φ(m). É possı́vel que ordm a = φ(m)? E se isso acontecer, será que isso é útil? Este
fato é tão útil que números com essa propriedade ganham um nome especial:
Definição 90. Dizemos que g é raiz primitiva de m quando ordm g = φ(m).
Um fato simples mas importante é que se g é uma raiz primitiva módulo m então as potências de g
“geram” todo o grupo (Z/mZ)× (daı́ a nossa escolha da letra g). Precisamente, temos
44
Lema 91. Se g é raiz primitiva de m então
(Z/mZ)× = {1, g, g 2 , . . . , gφ(m)−1 }
Ou seja, se (a, m) = 1 então existe i tal que a ≡ g i (mod m).
Demonstração. Como (Z/mZ)× tem φ(m) elementos, basta mostrar que dentre as φ(m) potências 1, g, g 2 , . . . , g φ(m)−1
de g não há duas repetidas módulo m. Mas se gi = gj para 0 ≤ i < j < φ(m) então gj−i = 1 com
0 < j − i < φ(m), contradizendo o fato de que g tem ordem φ(m).
Parece promissor, não? Pena que nem todos os números admitem raı́zes primitivas. O seguinte teorema
é o principal resultado deste capı́tulo:
Teorema 92 (Raı́zes Primitivas). Os números que admitem raı́zes primitivas são 2, 4, pn e 2pn , sendo p
primo ı́mpar.
A demonstração deste teorema é longa e será dada nas próximas seções. Vejamos antes alguns exemplos.
Exemplo 93. Seja p um primo. Mostre que
(
0
1 + 2 + · · · + (p − 1) mod p =
p−1
k
k
se (p − 1) ∤ k
se (p − 1) | k
k
Solução. Se (p − 1) | k, temos que cada termo da soma acima é congruente a 1 módulo p e o resultado
segue. Suponha agora que (p − 1) ∤ k e seja g uma raiz primitiva módulo p. Temos portanto
1k + 2k + · · · + (p − 1)k ≡ 1 + g k + g 2k + · · · + g (p−2)k
(mod p)
Gostarı́amos de “somar a PG módulo p” acima. Podemos utilizar o mesmo truque da soma da PG usual:
sendo S = 1 + g k + g 2k + · · · + g (p−2)k , multiplicando pela “razão g k ” e observando que g (p−1)k ≡ 1 (mod p)
temos
⇐⇒
⇐⇒
g k S ≡ g k + g 2k + · · · + g (p−1)k
k
k
2k
(mod p)
(p−2)k
g S ≡ 1 + g + g + ··· + g
(mod p)
k
k
g S ≡ S (mod p) ⇐⇒ (g − 1)S ≡ 0 (mod p)
Como g é uma raiz primitiva e (p − 1) ∤ k temos que g k − 1 6≡ 0 (mod p), assim pelo cancelamento obtemos
S ≡ 0 (mod p), o que encerra a prova.
Exemplo 94. Mostre que 2 é uma raiz primitiva módulo 3k para todo k ≥ 1.
Solução. Temos que mostrar que ord3k 2 = φ(3k ) = 2 · 3k−1 . A prova é por indução em k. O resultado
é verdadeiro para a base k = 1. Suponha agora que o resultado valha para k e seja d = ord3k+1 2. Pelo
“menor divide” temos que d | φ(3k+1 ) ⇐⇒ d | 2 · 3k . Por outro lado, como 2d ≡ 1 (mod 3k+1 ) =⇒ 2d ≡ 1
(mod 3k ) e ord3k 2 = 2 · 3k−1 por hipótese de indução, temos também que 2 · 3k−1 | d. Assim, só há duas
possibilidades para d: ou d = 2 · 3k−1 ou d = 2 · 3k . Devemos mostrar que a primeira não ocorre, ou seja,
k−1
que 22·3
6≡ 1 (mod 3k+1 ).
k−1
k−1
Mas isto é um trabalho para o lema de Hensel! Pelo lema, temos que 3k k 22·3
− 1, assim 22·3
6≡ 1
(mod 3k+1 ), o que encerra a prova.
45
O lema a seguir mostra como, a partir de uma raiz primitiva, encontrar todas as demais.
Lema 95. Seja g uma raiz primitiva módulo m. Mostre que as raı́zes primitivas de m são exatamente as
potências g i de g com (i, φ(m)) = 1. Em particular, m possui φ(φ(m)) raı́zes primitivas (se possuir alguma).
Solução. Como qualquer elemento de (Z/mZ)× é uma potência de g, temos que as raı́zes primitivas de
m também se escrevem como g i para algum i e a questão se resume a provar que ordm g i = φ(m) ⇐⇒
(i, φ(m)) = 1.
Seja d = (i, φ(m)) e t = ordm g i . Vamos provar que t = φ(m)/d, o que implica o lema. Primeiramente,
observe que como i/d ∈ Z temos
i/d
φ(m)/d
=1
= g φ(m)
gi
Assim, pelo “menor divide” temos que t divide φ(m)/d. Para mostrar que, reciprocamente, φ(m)/d divide
t, observe que como
t
g i = 1 ⇐⇒ g it = 1
|
e g é uma raiz primitiva, novamente pelo menor divide temos que φ(m) | it ⇐⇒ φ(m)
d
φ(m) i
φ(m)
( d , d ) = 1, pela alternativa de primo temos que d | t, completando a demonstração.
4.4
i
d
· t. Como
Demonstração do Teorema Principal
Vamos agora demonstrar o teorema acima. Começamos com uma pequena digressão sobre polinômios sobre
corpos finitos.
4.4.1
Polinômios com coeficientes em Z/pZ
Um corpo é um anel em que a multiplicação é comutativa e em que todo elemento não nulo possui inverso
multiplicativo. Por exemplo, Q, R e C são corpos, mas Z não. Uma questão natural é: quando Z/mZ é um
corpo?
Lema 96 (Corpo Finito). Z/pZ é um corpo se, e somente se, p é primo.
Demonstração. Se p é primo, então todo elemento com exceção de 0 é inversı́vel, logo Z/pZ é um corpo.
Reciprocamente, se Z/pZ é um corpo, os números 1, 2, . . . , p − 1 devem ser todos inversı́veis módulo p, isto
é, primos com p. Isto implica que p é primo (c.f. demonstração do teorema de Wilson).
Quando trabalhamos em um corpo K podemos fazer a divisão euclidiana de polinômios com coeficientes
em K utilizando o algoritmo da chave e o fato de que qualquer coeficiente não nulo ser inversı́vel. Por exemplo,
dividindo o polinômio x3 + 3x + 2 por 2x + 1 com coeficientes em Z/5Z obtemos quociente 3x2 + x + 1 e
resto 1:
2x + 1
x3 +0x2 +3x+2
−x3 −3x2
3x2 + x + 1
2x2 +3x+2
−2x2 −x
2x+2
−2x−1
1
Teorema 97. Seja f (x) um polinômio com coeficientes inteiros e de grau d e p um primo. Então a congruência f (x) ≡ 0 (mod p) tem no máximo d raı́zes módulo p, contando multiplicidades.
46
Demonstração. Indução em d. Para d = 0, não há raı́zes e para d = 1, o polinômio é da forma ax + b, a 6≡ 0
(mod p), cuja raiz é x = −b · a−1 mod p.
Seja f (x) de grau d e r uma raiz de f (caso f não tenha raı́zes, o teorema está demonstrado, pois d ≥ 0).
Então, pelo teorema do resto, f (x) ≡ (x − r)g(x) (mod p), sendo g de grau d − 1. Pela alternativa de primo,
temos que (x − r)g(x) ≡ 0 (mod p) ⇐⇒ x ≡ r (mod p) ou g(x) ≡ 0 (mod p). Pela hipótese de indução, g
tem no máximo d − 1 raı́zes, e o resultado segue.
Note que esse resultado não é válido para módulos compostos. Por exemplo, x2 − 1 ≡ 0 (mod 8)
tem 4 soluções, a saber, todos os ı́mpares módulo 8.

4.4.2
Enfim, a demonstração!
Vamos provar o teorema 92 em várias partes.
Lema 98. Se m tem dois fatores primos ı́mpares distintos p e q então m não admite raiz primitiva.
Demonstração. Se m admite dois fatores primos ı́mpares distintos p e q então podemos escrever m = a · b,
com (a, b) = 1, a, b > 1, p | a e q | b. Note que p − 1 | φ(a) e q − 1 | φ(b). Em particular, φ(a) e φ(b)
são ambos pares, ou seja, φ(a)/2 e φ(b)/2 são ambos inteiros. Assim, sendo x primo com m, xφ(a) ≡ 1
(mod a) =⇒ xφ(a)φ(b)/2 ≡ 1 (mod a). Analogamente, xφ(a)φ(b)/2 ≡ 1 (mod b). Como a e b são primos entre
si, concluı́mos que xφ(a)φ(b)/2 ≡ 1 (mod ab), de modo que ordm x ≤ φ(a)φ(b)/2 = φ(ab)/2 = φ(m)/2 < φ(m);
ou seja, m não admite raiz primitiva.
Lema 99. 2 e 4 admitem raiz primitiva, mas 2n , n ≥ 3, não.
Demonstração. Primeiro, 1 e 3 são raı́zes primitivas de 2 e 4, respectivamente. Seja x ı́mpar. Temos x2 ≡ 1
(mod 8) e, para n ≥ 3,
n−2
n−3
x2
− 1 = (x2 − 1)(x2 + 1)(x4 + 1) . . . (x2
+ 1)
i
n−2
tem pelo menos n fatores 2, já que 23 | x2 − 1 e 2 | x2 + 1, i = 1, 2, . . . , n − 3. Logo x2
≡ 1 (mod 2n ), ou
n−2
n
n
< φ(2 ) para todo x ı́mpar. Assim, 2 não admite raı́zes primitivas para n ≥ 3.
seja, ord2n x ≤ 2
Lema 100. Se 4 | m e m > 4 então m não admite raiz primitiva.
Demonstração. Seja m = 2k ℓ, ℓ ı́mpar e k ≥ 2. O caso ℓ = 1 já foi estudado no lema anterior. Nos demais
casos, basta repetir a demonstração do primeiro lema com 4 no lugar de p e q sendo um divisor de ℓ.
Lema 101. Todo primo ı́mpar p admite raiz primitiva.
Demonstração. Essa é a parte mais difı́cil do teorema e é aqui que utilizaremos o teorema sobre polinômios mod p. Considere o seguinte algoritmo para encontrar uma raiz primitiva de qualquer primo p:
Algoritmo
1. Tome a = 2.
2. Seja da = ordp a. Se da = p − 1, a é raiz primitiva de p; caso contrário, tome o menor número b que
não é congruente a algum ai mod p.
3. Seja db = ordp b. Se db = p − 1, b é raiz primitiva de p; se não, tome m e n tais que (m, n) = 1, m | da ,
n | db e mn = mmc(da , db ) (por que eles existem?).
4. Troque a por c = ada /m bdb /n e volte ao passo 2.
47
Vamos provar que esse algoritmo funciona e, o mais importante, termina. Supondo que termine, o
algoritmo funciona porque ele só para quando encontramos uma raiz primitiva.
Agora, provemos que o algoritmo termina, o que é mais interessante. Primeiro note que db não divide
da , pois se dividisse terı́amos bda ≡ 1 (mod p), o que não pode ocorrer pois a equação xda ≡ 1 (mod p)
admite no máximo da soluções, que são 1, a, a2 , . . . , ada −1 , e b não é congruente a nenhum ai . Isso implica
mmc(da , db ) > da . Além disso, seja k = ordp c. Então (ada /m bdb /n )k ≡ 1 (mod p). Elevando ambos os
membros por m, obtemos ada k bdb mk/n ≡ 1 (mod p) ⇐⇒ bdb mk/n ≡ 1 (mod p). Lembrando que db = ordp b,
pelo “menor divide” db | db mk/n ⇐⇒ n | mk. Sendo (m, n) = 1, temos n | k. Analogamente, m | k e,
portanto mn | k. Observando ainda que cmn ≡ 1 (mod p), temos ordp c = mn = mmc(da , db ) > da . Isto quer
dizer quem a cada iteração do algoritmo a ordem do próximo valor aumenta. Portanto, em algum momento
iguala o seu máximo, que é p − 1 (note que a escolha de b no algoritmo depende de ordp a 6= p − 1).
Lema 102. Se g é raiz primitiva de p mas não de p2 , então g + p é raiz primitiva de ambos.
Demonstração. Seja d = ordp2 g. Então
gd ≡ 1
(mod p2 ) =⇒ g d ≡ 1
(mod p) =⇒ p − 1 | d
Logo, como d 6= p(p − 1) e d | p(p − 1), d = p − 1, isto é, g p−1 ≡ 1 (mod p2 ).
2
Basta agora demonstrarmos que (g + p)p−1
6≡ 1 (mod 2p ). E esse é um trabalho para o binômio de
p−1 p−2
p−1
p−1
Newton! Temos (g + p)
≡ g
+ 1 g
p (mod p ) (você consegue ver por que não precisamos
escrever os demais termos do binômio de Newton?). Substituindo g p−1 ≡ 1 (mod p2 ) e desenvolvendo
obtemos (g + p)p−1 ≡ 1 + (p − 1)pg p−2 ≡ 1 − pg p−2 (mod p2 ), que não é 1, pois g p−2 6≡ 0 (mod p). Logo
g + p é raiz primitiva de p2 (e de p também!)
Lema 103. Se g é raiz primitiva de p e p2 então é raiz primitiva de pn , e portanto pn admite raiz primitiva.
Demonstração. Indução sobre n. A base de indução (n = 1 e n = 2) está na hipótese. Suponha que g seja
raiz primitiva de pn−1 . Seja d = ordpn g. Então
gd ≡ 1
(mod pn ) =⇒ g d ≡ 1
(mod pn−1 ) =⇒ ordpn−1 g | d =⇒ pn−2 (p − 1) | d
Como d | φ(pn ) ⇐⇒ d | pn−1 (p − 1), temos d = pn−2 (p − 1) ou d = pn−1 (p − 1). Para eliminar o primeiro
caso, vamos usar o lema de Hensel.
Note que como p | g p−1 − 1 e p2 não divide g p−1 − 1 (caso contrário, g não seria raiz primitiva de p2 ),
n−2
n−2
p k g p−1 − 1. Assim, pelo lema de Hensel, a maior potência de p que divide g p (p−1) − 1 = (g p−1 )p
−1
n−2
n−2
é p1+n−2 = pn−1 . Assim, pn não divide g p (p−1) − 1, o que é equivalente a g p (p−1) 6≡ 1 (mod pn ). Logo
ordpn g = pn−1 (p − 1) = φ(pn ) e, portanto, g é raiz primitiva de pn .
Lema 104. 2pn admite raiz primitiva.
Demonstração. Seja g uma raiz primitiva de pn . Note que φ(2pn ) = φ(pn ) (verifique!) e considere g ou
g + pn , o que for ı́mpar, e denote-o por h. Sendo d a ordem de h, temos hd ≡ 1 (mod 2pn ) =⇒ hd ≡ 1
(mod pn ) =⇒ φ(pn ) | d. Assim, d = φ(2pn ).
Ufa! Com isto, o teorema está provado!
4.5
4.5.1
Exercı́cios
Básicos
49. Encontre a ordem de
(a) 11 mod 190
(c) 5 mod 1024
(b) 7 mod 123
(d) 2 mod 343
48
50. Encontre todas as raı́zes primitivas de
(a) 11
(c) 10
(b) 23
(d) 50
51. Mostre que
(a) 2 é uma raiz primitiva de 11;
(b) 7 é uma raiz primitiva de 239;
(c) 2 é uma raiz primitiva de 5k para todo k.
52. Sejam x e y inteiros positivos. Prove que existem inteiros positivos m e n tais que m | x, n | y,
(m, n) = 1 e mn = mmc(x, y).
53. Prove o item (ii) do lema de Hensel.
4.5.2
Lição de Casa
54. (IMO) Os três últimos dı́gitos de 1978m são iguais aos três últimos dı́gitos de 1978n (1 ≤ m < n,
m, n ∈ N ). Determine m e n tais que m + n seja mı́nimo. (Cuidado! A resposta não é 1 + φ(1000)!!)
n
55. Mostre que se p é um primo tal que p | 22 + 1 então p ≡ 1 (mod 2n+1 ). Utilize este fato para encontrar
5
um fator primo de 22 + 1.
56. Sendo k ≥ 2 e n1 , n2 , . . . , nk ≥ 1 números naturais tais que n2 |2n1 − 1, n3 |2n2 − 1, . . . , nk |2nk−1 − 1 e
n1 |2nk − 1, mostre que n1 = n2 = · · · = nk = 1.
57. (OBM) Encontre todas as funções f : Z>0 → R tais que, para todos x, y inteiros não negativos,
f (x)f (y) = f (xy)
e
f (x + 1019) = f (x)
58. Seja f (x) um polinômio de coeficientes inteiros com grau d. Prove que a congruência f (x) ≡ 0 (mod p),
p primo, tem d soluções não congruentes entre si mod p se, e somente se, na divisão euclidiana de xp − x
por f (x), xp − x = f (x)q(x) + r(x), o resto r(x) tiver todos os seus coeficientes múltiplos de p.
59. Sendo k um inteiro positivo dado, encontre todos os inteiros positivos n tais que 7n + 1 é múltiplo de 5k .
60. Há outra maneira de provar que p admite raiz primitiva. Como? Siga os itens!
P
(a) Prove que d|n φ(d) = n. Dica: conte de duas maneiras a quantidade de pares (x, d) em que (x, n) = d.
(b) Prove que se d | p − 1 a congruência xd ≡ 1 (mod p) tem exatamente d soluções distintas mod p.
(c) Seja d um divisor de p − 1 e r(d) a quantidade de números mod p com ordem igual a d. Prove que
r(d) ≤ φ(d).
(d) Prove que, na verdade, r(d) = φ(d). Em particular, p admite φ(p − 1) raı́zes primitivas.
4.5.3
Questões de Prova
61. Encontre todos os números inteiros positivos n tais que x25 ≡ x (mod n) para todo inteiro x.
62. (IMO) Determine se existe um inteiro n com 2000 divisores primos distintos tal que n divide 2n + 1.
49
63. Encontre todos os inteiros m, n e p, onde p é um primo ı́mpar tais que
pm − np = 1
Dica: tente encontrar uma fatoração e calcule o mdc dos dois fatores da fatoração. Depois use o binômio de
Newton para concluir o problema.
64. (China) Encontre todos os inteiros não negativos x, y, z e w tais que
2x · 3y − 5z · 7w = 1
65. (IMO) Determine todos os inteiros n ≥ 1 tais que (2n + 1)/n2 seja inteiro.
66. (IMO) Determine todos os pares (n, p) de inteiros estritamente positivos tais que p é primo, n ≤ 2p e
(p − 1)n + 1 é divisı́vel por np−1 .
67. (Banco IMO) Encontre todas as ternas (a, m, n) de inteiros positivos tais que am + 1 divide (a + 1)n .
68. (Banco IMO) Seja a > 1 e m > n inteiros positivos. Prove que se am − 1 e an − 1 têm os mesmos
divisores primos então a + 1 é uma potência de 2.
69. (IMO Shortlist) Seja p > 3 um primo. Prove que existe a com 1 ≤ a < p − 1 tal que ap−1 − 1 e
(a + 1)p−1 − 1 não são divisı́veis por p2 .
50