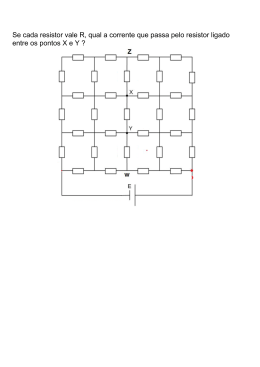
Universidade Federal do Pampa - UNIPAMPA
Exercı́cios Adicionais de Fı́sica III
Professor: Jorge Pedraza Arpasi,
Email: [email protected]
Para resolver estos exercı́cios, suponha que as unidades dos espaços R2 e R3 estejam em metros.
1. Considere o espaço R3 . Uma carga puntiforme de +2.3µC esta localizada na origem (0, 0, 0). Calcular o fluxo
através do tetraedro de vértices A = (−1, 1, −1), B = (1, 1, −1), C = (1, 1, 1), e D = (−1, 1, 1).
Resposta: 259887.0056497175 V.m
2. Uma linha infinita possui uma densidade de carga linear λ = 342 × 10−3 µC/m. Considere dois pontos p1 , p2
que distam a 1 metro e a 1.5 metros da linha. (a) Calcular a diferença de potencial entre p1 e p2 (b) Uma carga
⃗ gerado pela linha de
q = 3.6 × 10−10 C é deslocada do ponto p1 ao ponto p2 , calcular o trabalho do campo E
carga.
Resposta: 2493.27 Volts, 8.97 × 10−7 Joules .
3. Uma esfera condutora de 8 cm de raio possui uma carga de valor desconhecido. Sabendo-se que o campo
elétrico a distância de 17 cm do centro da esfera tem módulo igual a 2.0 × 102 N/C e aponta radialmente para
dentro, qual é a carga lı́quida na superfı́cie da esfera?
Resposta: 6.428090592 × 10−10 Coulombs .
4. Duas esferas concêntricas carregadas tem raios 10 cm e 15 cm. A esfera externa possui uma carga de +3×10−8 C
enquanto que a esfera interna tem +2 × 10−8 C. Determine o campo elétrico em (a) 12 cm e (b) 25 cm.
Resposta: 12488.58842743855 V/m, 7193.426934204602 V/m .
⃗ criado por uma carga pontual q0 = +3.0µC localizada
5. Considere o plano X −Y em metros, e o campo elétrico E
no ponto p0 = (1, 2). Considere os pontos p1 = (3, 3) e p2 = (4, −1). (a) Calcular a diferença de potencial
elétrico ∆V entre os pontos p1 e p2 . (b) Calcular a diferença de energia potencial elétrico ∆U entre os pontos
p1 e p2 para uma carga q1 = 3C.
Resposta: ∆V = 5704.461 Volts, ∆U = 17113.38 Joules .
6. No plano R2 considere uma carga pontual q localizada na origem (0, 0). Suponha que o potencial seja V (x, y) =
√ 22 2 . (a) Calcular o valor de q, (b)Pode existir esta carga na natureza? (c)Calcular o módulo e o sentido do
x +y
⃗ no ponto (1, 2). (d) Calcular a diferença de potencial entre os pontos p1 = (2, 3) e p2 = (−1, 5).
campo elétrico E
(e) Calcular a diferença de potencial entre os pontos (1, 0) e (−1, 0).
√ )
( √
⃗ 2) = 2 5, 4 5 Volts/metro ,
Resposta: q= 2.22469410456062 × 10−10 Coulombs, Sim, E(1,
25
25
√
√
1
2
∆V1 = − 13
26 + 13
13 Volts, ∆V2 = 0 Volts .
7. No plano R2 considere duas cargas pontuais q1 , q2 localizadas nos pontos p1 = (0, 0) e p2 = (4, 0). Suponha que
− √ 4562 2 . (a) Calcular os valores de q1 e q2 , (b)Calcular o módulo e o
o potencial seja V (x, y) = √ 123
2
2
x +y
(x−4) +y
⃗ no ponto (1, 2), (c) Calcular a diferença de potencial entre os pontos p1 = (2, 3) e
sentido do campo elétrico E
p2 = (−1, 5).
Resposta: q1 = 1.368187 × 10−8 Coulombs, q2 = 5.072303 × 10−8 Coulombs ,
⃗ 2)=(40.18722, 2.545733) Volts/metro, ∆V = −51.99173 Volts .
E(1,
(
⃗
E(x,
y) =
456(x − 4)
3
(y 2 + (x − 4)2 ) 2
−
123x
456y
123 y
3 ,
3 −
3
(y 2 + x2 ) 2 (y 2 + (x − 4)2 ) 2
(y 2 + x2 ) 2
)
8. Em R3 considere um campo elétrico definido pela função potencial: V (x, y, z) = √
2
4
−√
+
(x+1)2 +(y+1)2 +(z−3)2
x2 +y 2 +z 2
√
6
.
(x−3)2 +y 2 +(z−3)2
(a) Calcular os valores e as posições das cargas geradoras do campo, (b)Calcular o
⃗ no ponto (−2, 3, 1). (c) Calcular a diferença de potencial entre os pontos p1 = (2, −1, 3)
campo elétrico E
e p2 = (−1, 5, 5).
Resposta: q1 = 2.224694 × 10−10 Coulombs, q2 = −4.449388 × 10−10 Coulombs, q3 = 6.674082 × 10−10 Coulombs ,
⃗
E(−2,
3, 1) = (−0.1628646,
0.02512101,
0.07008298) Volts/metro ,
∆V = 2.901802 Volts .
⃗
9. Dado um campo elétrico definido por E(x,
y) =
(5, 5) e (−1, 2)
√
√
1
1
Resposta: ∆V = − 29
29 + 20
5 volts
(x−2,y+3)
,
(x2 −4x+y 2 +6y+13)3/2
calcular a diferença de potencial entre