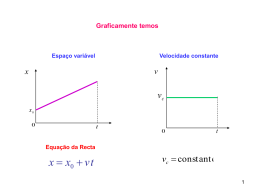
QUEDA LIVRE
 Corpos em queda livre
 Equações do movimento de queda livre
1
Corpos em queda livre
Galileo, o primeiro físico moderno, estudou a queda dos corpos
Refutou as hipóteses de Aristóteles
2
Através de experiências, Galileu mostrou que os corpos caem com a mesma
velocidade, independentemente de sua massa:
x ~ t2 e v ~ t ; conseqüências de uma aceleração constante!
Lembrar que

1
x  x0  v0t  at 2
2
e
v  v0  at
Exemplos de corpos em queda livre
3
Corpos em queda livre
Mas... devemos notar que em
geral, há outras forças atuando no
corpo considerado, o que pode
frustrar uma experiência se não
formos suficientemente cuidadosos
a
resistência
do ar!!
Força de atrito do ar!!!!
4
Queda livre de um elefante e de uma pena
No ar
No vácuo
5
Queda livre no vácuo
6
Corpos em queda livre
Vector aceleração da gravidade


g

g
O vector g aponta para baixo em
direção ao centro da Terra
Valor da aceleração da gravidade
perto da superfície da Terra
g  9.8 m/s 2
Para estudar um corpo em queda livre, consideramos que :
• a aceleração g é constante durante o intervalo do movimento e direcionada
para baixo
• o efeito da resistência do ar é desprezável
7
Corpos em queda livre
y

v0

g

g


g   gey

ey
As equações obtidas para partículas em movimento com aceleração constante
(MRUV) são aplicáveis ao corpo em queda livre. Assim
v  v0  at
1 2
x  x0  v0t  at
2


v  v0  gt
y  y0  v0t 
1 2
gt
2
8
Exemplo 1: Um corpo cai livremente a partir do repouso; calcule a sua
posição e velocidade em t = 1.0, 2.0 e 3.0 s.
Resolução
1 2
y   gt
2
e v   gt
Em t = 1.0 s:
y = - 4.9 m
e
v = -9.8m/s
Para outros valores do tempo, obtemos:
9
y
Exemplo 2. Uma pedra é arremessada verticalmente para cima no
ponto A do terraço de um edifício com uma velocidade inicial de 20.0
m/s. O prédio tem 50.0 m de altura. Determine: a) o tempo no qual a
pedra atinge a sua altura máxima, b) a altura máxima acima do
terraço e c) o tempo no qual a pedra retorna ao nível do arremessador.
a) o tempo no qual a pedra atinge a sua altura máxima
Quando a pedra atinge a altura máxima ela pára e
v  v0  gt
então v=0 no ponto máximo
Substituindo o valor de v na equação fica
0  v0  gt

v0  gt

v0 20.0 m/s
t 
 2.04 s
2
g 9.8 m/s
b) a altura máxima acima do terraço
1
y0  0
t  2.04 s
y  y0  v0t  gt 2
2
Substituindo na equação fica
1
y  (20 m/s)(2.04 s)  (9.8 m/s 2 )( 2.04 s) 2  20.4 m
2
c) o tempo no qual a pedra retorna ao nível do arremessador
1
 t 0
1 2
1
y  y0  v0t  gt 2
0  v0t  gt  (v0  gt)t 
2
y0  0
y0
2
2
t  4.08 s
10