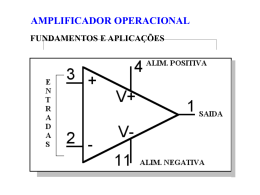
AMPLIFICADORES
OPERACIONAIS
FUNDAMENTOS
6h
AMP-OP IDEAL
O modelo de um amplificador operacional
(AMP-OP) ideal é mostrado a seguir.
 Um AMP-OP é na verdade um amplificador
diferencial com tensão de saída dada por:
vO=A(v2-v1)
 onde A é o ganho do AMP-OP, que
idealmente vale , v2 é a tensão no terminal
não-inversor e v1 é a tensão no terminal
inversor.

2
AMP-OP IDEAL
3
AMP-OP IDEAL
Como o ganho de malha aberta é infinito, e
dado que o AMP-OP não esteja saturado, as
tensões nos terminais de entrada são iguais,
ou seja:
v2=v1
 Além disso, a impedância dos terminais de
entrada é idealmente . Desse modo, a
corrente que entra nestes terminais é nula.

4
CONFIGURAÇÃO
INVERSORA
Considere o amplificador OP-AMP na
configuração inversora, mostrado a seguir.
 Dado que o terminal não-inversor está
aterrado, então teremos um terra virtual no
terminal inversor.
 Desprezando a corrente no terminal
inversor, podemos escrever que:
vI/R1=-vO/R2 e portanto,
Gv=vO/vI=-R2/R1

5
CONFIGURAÇÃO
INVERSORA
6
EFEITO DO GANHO FINITO
Neste caso, ao invés do terra virtual, termos
uma tensão de
v1=-vO/A
 E portanto,
(vI+vO/A)/R1=-(vO+vO/A)/R2
 E portanto,
Gv=vO/vI=-(R2/R1)/[1+1/A+R2/(R1A)]
desde que (1+R2/R1)/A<<1.

7
EXEMPLO DO EFEITO DO
GANHO FINITO
Considere a configuração inversora com
R1=1 k e R2=100 k.
 Calcule o ganho de malha fechada para os
casos em que:
– A=103
– A=104
– A=105
 e compare com o ganho supondo AMP-OP
ideal.

8
EXEMPLO DO EFEITO DO
GANHO FINITO

O ganho de malha fechada supondo um
AMP-OP ideal é igual a Gv=-R2/R1=-100.
–
–
–

Para A=103, Gv=-90,83, erro de 9%
Para A=104, Gv=-99,00, erro de 1%
Para A=105, Gv=-99,90, erro de 0,1%
AMP-OPs práticos têm ganhos de malha
aberta superiores a 105.
9
RESISTÊNCIA DE
ENTRADA E DE SAÍDA
Supondo configuração inversora e um
AMP-OP de ganho de malha aberta infinito,
isto significa que teremos na entrada
inversora um terra virtual e portanto a
resistência de entrada é:
Ri=R1
 Como temos na saída uma fonte de tensão,
então a resistência de saída vale:
Ro=0

10
EXEMPLO DE AMP-OP
Obtenha o ganho de malha fechada para o
AMP-OP na configuração mostrada a
seguir.
 A seguir, projete um amplificador inversor
com:
– Gv=100
– Ri=1 M
com a condição de que todos os resistores
do circuito devem ser menores que 1 M.

11
EXEMPLO DE AMP-OP
12
EXEMPLO DE AMP-OP

Escrevendo que:
i1=0
iI=vI/R1
i2=i1
i2+i3=i4
i2=-vx/R2
i3=-vx/R3
i4=(vx-vO)/R4
13
EXEMPLO DE AMP-OP
Que se reduzem a duas equações:
vI/R1=-vx/R2
-vx/R2-vx/R3=(vx-vO)/R4
 E portanto,
vO/vI=-(R2/R1)(1+R4/R2+R4/R3)
 Quem determina a resistência de entrada é
R1, assim:
R1= 1 M

14
EXEMPLO DE AMP-OP
A partir daí temos 3 incógnitas e 1 equação.
Assim sendo, o número de soluções é
infinito.
 Uma delas é:
– R2=1 M
– R4=1 M
– R3=10,2 k
que satisfazem o valor da máxima
resistência de 1 M.

15
CIRCUITO SOMADOR
Considere o circuito a seguir.
 Como
i1=v1/R1, i2=v2/R2, ... , in=vn/Rn
i=i1+i2+...+in
vo=-Rfi
 Portanto,
vo=-(Rf/R1)v1-(Rf/R2)v2-...-(Rf/Rn)vn

16
CIRCUITO SOMADOR
17
CIRCUITO SOMADOR E
SUBTRATOR
18
AMPLIFICADOR NÃOINVERSOR
Considere a configuração a seguir.
 Supondo AMP-OP ideal, a tensão de
entrada aparecerá na entrada inversora.
 Assim, a corrente em R1 é igual àquela em
R2, ou seja:
vI/R1=(vO-vI)/R2
 E portanto,
Av=vO/vI=1+R2/R1

19
AMPLIFICADOR NÃOINVERSOR
20
RESISTÊNCIA DE
ENTRADA E DE SAÍDA
Supondo AMP-OP ideal, a resistência de
entrada é:
Ri=
pois não existe corrente nos terminais de
entrada.
 Como a saída é tomada de uma fonte de
tensão, temos que:
Ro=0

21
EFEITO DO GANHO DO
AMP-OP FINITO

Pode-se mostrar que o ganho da
configuração não-inversora, considerando
um AMP-OP de ganho A, é dado por:
Av=(1+R2/R1)/[1+(1+R2/R1)/A]
22
CIRCUITO SEGUIDOR DE
TENSÃO

Fazendo na configuração não-inversora R1=
 e R2=0, temos que:
vO=vI
ou seja, temos um amplificador de ganho
unitário e alta impedância de entrada.
23
CIRCUITO SEGUIDOR DE
TENSÃO
24
AMPLIFICADOR DE
DIFERENÇAS
Pode-se mostrar que para o amplificador da
próxima figura:
vo=(R2/R1)(v2-v1)
 Como desvantagem deste circuito, temos
que as resistências de entradas não são
iguais:
Ri1=R1
Ri2=R1+R2
 E cujos valores não são necessariamente
altos.

25
AMPLIFICADOR DE
DIFERENÇAS
26
AMPLIFICADOR DE
INSTRUMENTAÇÃO




O próximo amplificador tem altíssima resistência
de entrada.
Podemos escrever que:
vo1=(1+R2/2R1)v1-(R2/2R1)v2
vo2=-(R2/2R1)v1+(1+R2/2R1)v2
vo1-vo2=(1+R2/R1)(v1-v2)
E também que:
vo=-(R4/R3)(vo1-vo2)
Portanto, o ganho de tensão é dado por:
vo=(R4/R3)(1+R2/R1)(v2-v1)
27
AMPLIFICADOR DE
INSTRUMENTAÇÃO
28
EFEITO DO GANHO FINITO E DA
BANDA DO AMP-OP
Considere a curva de ganho de tensão típico
de malha aberta em função da frequência,
mostrada a seguir.
 Em analogia aos circuitos RC passa-baixas,
podemos escrever que:
Av(jf)=A0/(1+jf/fb)
onde A0 é o ganho na faixa de passagem e fb
é a frequência de corte.

29
EFEITO DO GANHO FINITO E DA
BANDA DO AMP-OP
30
EFEITO DO GANHO FINITO E DA
FAIXA DE PASSAGEM DO AMP-OP
Para altas frequências, podemos escrever
que f/fb>>1, e portanto o módulo:
|Av(f)|=A0fb/f
 Chamaremos a frequência em que o ganho é
unitário de ft. Portanto,
ft=A0fb
 Tipicamente, A0=105, fb=10 Hz.
Portanto, ft=1 MHz.

31
RESPOSTA EM FREQUÊNCIA
DE AMPLIFICADORES
Um amplificador inversor tem ganho de
malha fechada:
Vo/Vi=-(R2/R1)/[1+(1+R2/R1)/Av]
onde
Av(jf)=A0/(1+jf/fb)
 Portanto, desde que A0>>1+R2/R1,
Vo/Vi (jf)=-(R2/R1)/(1+jf/f0)
onde f0 é a frequência de corte, dada por:
f0=ft/(1+R2/R1)

32
RESPOSTA EM FREQÜÊNCIA
DE AMPLIFICADORES
Um amplificador não-inversor tem ganho
de malha fechada:
Vo/Vi=(1+R2/R1)/[1+(1+R2/R1)/Av]
onde
Av(jf)=A0/(1+jf/fb)
 Portanto, desde que A0>>1+R2/R1,
Vo/Vi(jf)=(1+R2/R1)/(1+jf/f0)
onde f0 é a frequência de corte, dada por:
f0=ft/(1+R2/R1)

33
EXEMPLO DE
FREQUÊNCIA DE CORTE

Considere um AMP-OP com ft=1 MHz.
Calcule a frequência de corte para ganhos
de
–
–
–
–
1000
100
10
1
34
EXEMPLO DE
FREQÜÊNCIA DE CORTE
Ganho em Malha Fechada
fo
1000
1 kHz
100
10 kHz
10
100 kHz
1
1 MHz
 Pode-se observar que o produto ganhobanda é constante.

35
SATURAÇÃO DA TENSÃO
DE SAÍDA

Tipicamente, os níveis de saturação de um
amplificador operacional estão localizados
no intervalo:
Vcc-3L+  Vcc-1
-Vcc+1  L-  -Vcc+3
36
SATURAÇÃO DA
CORRENTE DE SAÍDA

AMP-OPs possuem saturação da corrente
de saída. Por exemplo, o AMP-OP 741
possui corrente máxima de ±20 mA. Se esta
corrente for ultrapassada, a tensão de saída
irá saturar.
37
TAXA MÁXIMA DE VARIAÇÃO DA
TENSÃO DE SAÍDA – “SLEW-RATE”
Para grandes sinais, existe um fenômeno
não linear que limita a taxa máxima de
variação do sinal de saída, conhecido como
“slew-rate”, e definido por:
SR=vO/t
 Supondo que se tenha na entrada um sinal
senoidal:
vI=Visen(2ft)

38
“SLEW-RATE”
39
“SLEW-RATE”



A sua derivada é dada por:
vI/t=2fVicos(2ft)
cujo valor máximo de 2fVi ocorre nos pontos de
cruzamento de zero.
Se o valor máximo da derivada ultrapassar o
“slew-rate” do AMP-OP, a saída será distorcida,
como mostrado na figura a seguir.
Usualmente, os catálogos indicam a frequência de
passagem a plena potência, dada por:
fM=SR/(2VO,max)
40
“SLEW-RATE”
41
TENSÃO DE “OFFSET”
Mesmo conectando os pinos de entrada
entre si e também ao terra, a saída irá
saturar para o lado positivo, ou negativo.
 Isto ocorre devido a um desequilíbrio
presente no estágio de entrada, que faz com
que exista uma diferença de tensão entre os
pinos de entrada.
 Valores típicos desta tensão de “offset”
estão entre 1 e 5 mV.

42
TENSÃO DE “OFFSET”
43
TENSÃO DE “OFFSET”
Para amplificadores com ganhos pequenos e
acoplamento DC na entrada, ou
amplificadores com ganhos grandes e
acoplamento AC, a tensão de “offset” não é
problema.
 Para amplificadores com ganhos grandes e
acoplamento DC, a tensão de “offset” pode
ser cancelada utilizando os terminais de
anulação de “offset”.

44
TENSÃO DE “OFFSET”
45
ACOPLAMENTO AC
Utilizando acoplamento AC, como pela
inserção de um capacitor em série, o
problema da tensão de “offset” pode ser
superado.
 No entanto, a malha composta por C e por
R1, forma um filtro passa-altas com
frequência de corte dada por:
fc=1/(2R1C)
e que impede um ganho da tensão de
“offset”.

46
ACOPLAMENTO AC
47
CORRENTES DE
POLARIZAÇÃO DE ENTRADA
Um AMP-OP real apresenta correntes de
polarização de entrada não-nulas, conforme
pode ser visto a seguir, onde o valor médio:
IB=(IB1+IB2)/2
 A diferença entre as correntes de
polarização é denominada de corrente de
“offset” de entrada.
IOS=|IB1-IB2|

48
CORRENTES DE
POLARIZAÇÃO DE ENTRADA
49
CORRENTES DE
POLARIZAÇÃO DE ENTRADA
Pode-se mostrar que a tensão de saída de
um amplificador inversor é dada por:
VO=IB1R2
que obviamente estabelece um valor
máximo para R2.
 A conexão de um resistor R3 na entrada
não-inversora, mostrado a seguir, ajuda a
diminuir o efeito da corrente de polarização
na tensão de saída.

50
CORRENTES DE
POLARIZAÇÃO DE ENTRADA
51
CORRENTES DE
POLARIZAÇÃO DE ENTRADA
A equação de corrente no pino inversor
pode ser escrita como:
IB2R3/R1+(VO+IB2R3)/R2=IB1
 Isolando VO, temos que:
VO=IB1R2-IB2(R3+R2R3/R1)
 Supondo IB1=IB2=IB, a tensão pode ser
reduzida a zero, desde que
R3=R1R2/(R1+R2)

52
CORRENTES DE
POLARIZAÇÃO DE ENTRADA
Supondo agora, que IB1IB2, ou seja
IB1=IB+IOS/2
IB2=IB-IOS/2
 Usando o valor de R3 ótimo, e substituindo
na equação da tensão de saída, temos que:
VO=IOSR2
onde IOS é apreciavelmente menor que IB.

53
AMPLIFICADORES COM
ACOPLAMENTO AC
Para o circuito inversor com acoplamento
AC, R3 deve ser igual a resistência DC vista
pelo terminal inversor, ou seja R2.
 Para o circuito não-inversor com
acoplamento AC, R3 também é igual a R2 e
ele é imprescindível, pois ele garante a
polarização do estágio de entrada conectado
à entrada não-inversora.

54
AMPLIFICADOR INVERSOR
COM ACOPLAMENTO AC
55
AMPLIFICADOR NÃO-INVERSOR
COM ACOPLAMENTO AC
56
CONFIGURAÇÃO INVERSORA
COM IMPEDÂNCIAS
57
EXEMPLO DE AMPLIFICADOR
COM FILTRO PASSA-BAIXAS
Obtenha a função de transferência do
circuito da próxima figura.
 Obtenha o ganho DC e a frequência de
corte.
 Projete o circuito para que o ganho DC seja
de 40 dB, a frequência de corte 1 kHz e a
resistência de entrada 1 k.

58
EXEMPLO DE AMPLIFICADOR
COM FILTRO PASSA-BAIXAS
59
EXEMPLO DE AMPLIFICADOR
COM FILTRO PASSA-BAIXAS



Podemos escrever que:
Vo(j)/Vi(j)=-Z2(j)/Z1(j)
onde Z2(j )=R2/(1+jR2C2) e Z1(j)=1/(jC1)
Portanto
Vo(j)/Vi(j)=-(R2/R1)/(1+jR2C2)
O ganho, a frequência de corte e a impedância de
entrada são dados por:
Av=-R2/R1
f0=1/(2R2C2)
Zi=R1
60
EXEMPLO DE AMPLIFICADOR
COM FILTRO PASSA-BAIXAS
A partir do valor de impedância de entrada,
temos que R1=1 k
 Além disso, sabemos que 40 dB de ganho
de tensão é o mesmo que |Gv|=100, portanto
R2=|Gv|R1
e assim R2=100 k.
 A partir da frequência de corte, temos que
C2=1/(2R2f0)
e portanto, C2=1,6 nF.

61
CIRCUITO INTEGRADOR
INVERSOR
Considere o integrador de Miller.
 Observe que
i1(t)=vI(t)/R
CvC(t)/t=i1(t)
vo(t)=-vC(t)
 Portanto,
vo(t)=-1/(RC)0t vI(t)dt-VC(0)
onde VC(0) é a tensão no capacitor em t=0.

62
CIRCUITO INTEGRADOR
INVERSOR
63
CIRCUITO INTEGRADOR
INVERSOR
Chamando Z1=R e Z2=XC, temos que:
Vo(j)/Vi(j)=-1/(jRC)
 Assim, a função de transferência de
magnitude:
|Vo()/Vi()|=1/(RC)
 E a de fase:
arg[Vo()]-arg[Vi()]=90°

64
EXEMPLO DE
INTEGRADOR MILLER
Obtenha na saída de um integrador Miller a
resposta a um pulso de 1 V de amplitude e
duração 1 ms. Suponha que R=10 k, C=10
nF e que o capacitor encontra-se
descarregado.
 A integral de um pulso retangular produz
uma rampa. Como RC=10-4 s e o valor da
integral é 10-3 Vs, concluímos que o valor
de pico da rampa é igual a 10 V.

65
EXEMPLO DE
INTEGRADOR MILLER
66
INTEGRADOR COM
TENSÃO DE “OFFSET”
Outro circuito que é bastante afetado pela
tensão de “offset” é o integrador Miller.
 Pode-se mostrar que a tensão de saída é
dada por:
vO(t)=VOS+1/(RC)0t VOSdt
que leva a saída para a saturação.
 A colocação de um resistor em paralelo com
o capacitor resolve o problema da saturação.

67
INTEGRADOR COM
TENSÃO DE “OFFSET”
68
CIRCUITO DIFERENCIADOR
INVERSOR
Considere o circuito a seguir.
 Observe que
vI(t)=vC(t)
i1(t)=iC(t)
C(vC(t)/t)=iC(t)
vo(t)=-iC(t)R
 Portanto,
vo(t)=-RC vI(t)/t

69
CIRCUITO DIFERENCIADOR
INVERSOR
70
CIRCUITO DIFERENCIADOR
INVERSOR
Chamando Z1=XC e Z2=R, temos que:
Vo(j)/Vi(j)=-jRC
 Assim, a função de transferência de
magnitude:
|Vo()/Vi()|=RC
 E a de fase:
arg[Vo()]-arg[Vi()]=-90°

71