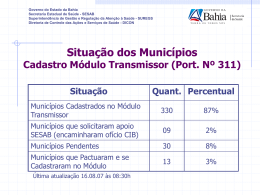
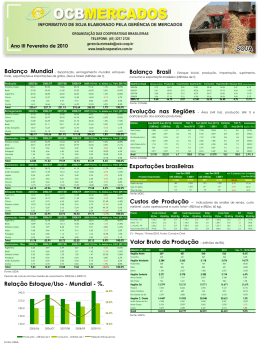
Capítulo 4 – Métodos de
Suavização Exponencial
Gueibi Peres Souza
Robert Wayne Samohyl
Rodrigo Miranda
Introdução
• Métodos de suavização exponencial:
– Utilizam apenas dados da própria série para
fazer previsões, como decomposição clássica.
– As previsões são feitas de forma rápida
– Melhores resultados para previsões de curto
prazo
Introdução
• O que será visto:
– Suavização exponencial simples
– Método de Holt
– Método de Holt – Winters
– Classificação Geral dos métodos
exponenciais
– Métodos com tendência amortecida
Pesos atribuídos as observações passadas
para diversos métodos de previsão
Métodos Univariados
Previsão Ingênua
Média Simples
Previsão por
Suavização
Exponencial
100% do Peso a
observação anterior
Todas as observações
passadas recebem
o mesmo peso
Os pesos atribuídos as
observações passadas
decaem exponencialmente
Suavização Exponencial Simples
(simplória)
• Método para séries sem tendência e sem sazonalidade
observado
NN
tempo
Para todas as
possibilidades de
padrões de séries, veja
SES – equação
(demonstração matemática e exemplos
numéricos passo a passo do capítulo 4 não constam nesta apresentação, desculpe!)
• Previsão (amanha) = peso*valor observado hoje
+ (1-peso)*valor previsto para hoje
Pt+1 = αOt + (1-α)Pt
(4.3)
• Onde:
– Pt é a previsão no período t
– Ot é o valor observado no período t
– α é a constante de suavização que varia entre 0 e 1.
• A previsão de Pt+1 é uma combinação do
observado com o previsto em t
Demonstração da suavização exponencial
simples. O valor previsto depende de todos os
valores passados.
Pt+1 = αOt + (1-α)Pt
Pt = αOt-1 + (1-α)Pt-1
Pt+1 = αOt + (1-α)[αOt-1+(1-α)Pt-1]
Pt+1 = αOt + α(1-α)Ot-1+(1-α)2Pt-1
Pt+1 = αOt + α(1-α)Ot-1+α(1-α)2Ot-2+ α(1-α)3Ot-3+...
+ α(1-α)t-1O1+(1-α)tP1
(4.5)
SES – Interpretando a equação
Pt+1 = αOt + α(1-α)Ot-1+α(1-α)2Ot-2+ α(1-α)3Ot-3+...+ α(1-α)t-1O1+(1-α)tP1
• a previsão (Pt+1) depende de todos os valores
observados, do mais recente (Ot) até o mais velho O1
• Quando α = 1, então Pt+1 = Ot e o método passa a ser
igual ao método ingênuo
• se α = 0 então Pt+1 = P1 e o método utiliza a previsão do
primeiro período para prever todos os outros períodos.
SES – Pesos atribuídos as observações passadas
despendendo do valor de α (tabela 4.2)
Peso
Ano / Período
eq. 4.5
α = 0,2
α = 0,5
α = 0,8
2005 / Ot-1
α
0,200
0,500
0,800
2004 / Ot-2
α (1 – α)
0,160
0,250
0,160
2003 / Ot-3
α (1 – α)2
0,128
0,125
0,032
2002 / Ot-4
α (1 – α)3
0,102
0,062
0,006
2001 / Ot-5
α (1 – α)4
0,081
0,031
0,001
2000 / Ot-6
α (1 – α)5
0,065
0,015
0,000
1999 / Ot-7
α (1 – α)6
0,052
0,007
0,000
1998 / Ot-8
α (1 – α)7
0,041
0,003
0,000
1997 / Ot-9
α (1 – α)8
0,033
0,001
0,000
1996 / Ot-10
α (1 – α)9
0,026
0,000
0,000
1995 / P1
(1 – α)10
0,107
0,000
0,000
SES – Pesos atribuídos as observações
passadas despendendo do valor de α (gráficos)
α = 0.2
α = 0.5
0,25
0,6
0,200
0,2
0,160
0,15
0,4
0,128
0,107
0,042 0,052
0,027 0,034
0,05
0,3
0,102
0,1
0,066
0,500
0,5
0,250
0,082
0,2
0,1
0
0,125
0,031
0,001 0,001 0,002 0,004 0,008 0,016
0,063
0
t-11
t-10
t-9
t-8
t-7
t-6
t-5
t-4
t-3
t-2
t-1
t-11
t-10
t-9
t-8
α = 0.8
0,9
0,800
0,8
0,7
0,6
0,5
0,4
0,3
0,160
0,2
0,1 0,000 0,000 0,000 0,000 0,000 0,000 0,001 0,006 0,032
0
t-11 t-10
t-9
t-8
t-7
t-6
t-5
t-4
t-3
t-2
t-1
t-7
t-6
t-5
t-4
t-3
t-2
t-1
SES – Análise dos gráficos
α=
Suavização
α=
Suavização
• O procedimento para encontrar α é definido através de
algum critério que minimize as discrepâncias de
ajustamento (Pt – Ot), como o DQM (Discrepância
quadrada média) ou o DPAM (Discrepância percentual
absoluta média)
SES – Exemplo (tabela 4.1) para vários
valores de α (figura 4.3)
270.000
250.000
230.000
210.000
190.000
170.000
150.000
130.000
1996
1998
vendas Gol 1000
2000
alfa = 0,2
2002
alfa = 0,5
2004
2006
alfa = 0,8
SES – Exemplo Produção Anual de
Café
1000 ton
Resultados do exemplo: DM = 4,8, DPAM = 20,32% e
U de Theil = 0,64
5.000
4.500
4.000
3.500
3.000
2.500
2.000
1.500
1.000
500
0
1980
1985
1990
Observado
1995
2000
Modelo para alfa = 0,01
2005
Conceito de Nível
• Nível é onde a observação está no período t
• Todas as observações da série1 possuem um nível de
10 unidades
• Todas as observações da série 2 possuem um nível de
7 unidades
450.000
400.000
350.000
300.000
250.000
200.000
150.000
100.000
50.000
0
1970
1975
1980
1985
Observado
1990
1995
2000
2005
Modelo para alfa = 0,99
2004
2002
2000
1998
1996
1994
1992
1990
1988
1986
1984
1982
1980
1978
1976
1974
1972
25.000
20.000
15.000
10.000
5.000
0
-5.000
-10.000
-15.000
-20.000
-25.000
-30.000
1970
• o crescimento médio da série
é de aproximadamente 10.000
GWh ao ano
• quase todas as discrepâncias
são negativas, a única
exceção ocorre em 2001,
quando houve o racionamento
de energia elétrica
• As medidas de ajuste de
método para este caso foram:
DM = -10.269(indicação de
viés nas previsões), DPAM =
7,15% e U de Theil = 1,01
Energia (GWh)
Por que a SES não funciona em dados com
tendência – exemplo (tabela 4.4).
Método de Holt
observado
• O método de Holt foi desenvolvido para dados que apresentem
tendência.
tempo
Para todas as
possibilidades de
padrões de séries, veja
Nível e Crescimento para o
método de Holt
• Níveis diferentes com crescimento igual
• Nível S1,1 = 11; nível S1,2 = 12 ;Crescimento c1,1 = S1,2 - S1,1 = 1
• Nível S2,1 = 6; nível S2,2 = 7 ;Crescimento c2,1 = S2,2 – S2,1 = 1
Nível e Crescimento para o
método de Holt
• Níveis diferentes com crescimento
diferente
• Nível S1,1 = 13; nível S1,2 = 16 ;Crescimento c1,1 = S1,2 - S1,1 = 3
• Nível S2,1 = 6; nível S2,2 = 7 ;Crescimento c2,1 = S2,2 – S2,1 = 1
Cada período possui nível
diferente,
cada dois períodos tem
crescimento diferente.
Método de Holt – Exemplo (tabela 4.5):
Produção anual de energia elétrica
• α = 0,99 e β = 0,01
• Resultados do exemplo: DM = -1.228 , DPAM = 2,82% e
Energia (GWh)
U de Theil = 0,42
450.000
400.000
350.000
300.000
250.000
200.000
150.000
100.000
50.000
0
1970
1975
1980
1985
Observado
• Figura 4.9
1990
1995
Ajustado
2000
2005
Nível e Crescimento para o
método de Holt
Exemplo (tabela 4.5) - Comparando
discrepâncias da SES com Holt
450.000
400.000
350.000
300.000
250.000
200.000
150.000
100.000
50.000
0
1970
SES
Energia (GWh)
Energia (GWh)
Holt
1975
1980
1985
Observado
1990
1995
2000
2005
450.000
400.000
350.000
300.000
250.000
200.000
150.000
100.000
50.000
0
1970
Ajustado
30000
20000
20000
10000
10000
-10000
-20000
19
70
19
73
19
76
19
79
19
82
19
85
19
88
19
91
19
94
19
97
20
00
20
03
-30000
1980
Observado
30000
0
1975
1985
1990
1995
2000
2005
Modelo para alfa = 0,99
0
-10000
-20000
-30000
1970 1973 1976 1979 1982 1985 1988 1991 1994 1997 2000 2003
Exemplo (tabela 4.5) - Comparando a
SES com Holt
10
11
9
3
0
00
0
25
0
00
1
0
00
20
0
15
00
00
0
10
0
0
0
50
0
1
00
-2 0
00
0
-1 0
50
0
-1 0
00
00
-5
00
0
12
10
8
6
4
2
0
-2
5
Observações
Histograma Holt
Histograma SES
14
15
10
10
6
5
3
0
1
0
0
0
1
0
0
0
00
00
25
0
20
00
0
15
00
0
00
10
50
0
-2 0
00
0
-1 0
50
0
-1 0
00
00
-5
00
0
0
-2
50
Observações
• Observando os dois
histogramas percebe-se um
viés nas discrepâncias da
SES (entre -10000 e -5000),
enquanto que no método de
Holt as discrepâncias estão
em torno de 0.
Por que o método de Holt não funciona em dados
com sazonalidade – exemplo (tabela 4.6)
2062330,19
1962330,19
1862330,19
1762330,19
1662330,19
1562330,19
1462330,19
1362330,19
1262330,19
dez/99
abr/01
set/02
jan/04
Observado
mai/05
Previsto
out/06
200000.00
fev/08
Ajustado
300000.00
fev/06
fev/03
fev/01
fev/04
fev/02
fev/05
100000.00
0.00
-100000.00
-200000.00
-300000.00
dez/02
dez/05
dez/01
set/06
mai/06
jan/06
mai/05
jan/05
set/04
dez/04
mai/04
jan/04
mai/03
jan/03
set/02
mai/02
jan/02
set/01
jan/01
set/03
dez/03
-500000.00
set/05
-400000.00
mai/01
• α = 0,01 e β = 0,89
• Com o valor de α = 0,01, a
sazonalidade é suavizada ao
invés de ter os seus índices
calculados. O mês de
dezembro, por exemplo, tem
um número de consultas de
aproximadamente 23% maior
que a média do ano e o de
fevereiro um número de 12 %
abaixo
• As medidas de ajuste de
método para este caso foram:
DPAM = 6,45% e U de Theil =
0,744
Método de Holt – Winters com
sazonalidade Aditiva
observado
• O método de Holt – Winters foi desenvolvido para dados que
apresentas tendência e sazonalidade
tempo
Para todas as
possibilidades de
padrões de séries, veja
Método de Holt – Winters com
sazonalidade Multiplicativa
observado
• Este é o método de previsão em que ocorrem mais
casos, portanto é o mais utilizado.
tempo
Para todas as
possibilidades de
padrões de séries, veja
Método de Holt – Winters aditivo – Exemplo
(tabela 4.7): Número de consultas ao SPC
• α = 0,37, β = 0,01 e γ = 0,01
• Resultados do exemplo: DM = 1.804 , DPAM = 2,56% e U de Theil
= 0,26
2.162.330
2.062.330
1.962.330
1.862.330
1.762.330
1.662.330
1.562.330
1.462.330
1.362.330
1.262.330
dez/99
abr/01
set/02
Observado
jan/04
Previsto
mai/05
out/06
Ajustado
fev/08
Exemplo (tabela 4.7) - Comparando Holt com Holt - Winters
2.162.330
2062330,19
2.062.330
1.962.330
1962330,19
1862330,19
1.862.330
1.762.330
1762330,19
1.662.330
1.562.330
1662330,19
1562330,19
1.462.330
1.362.330
1462330,19
1362330,19
1262330,19
dez/99
abr/01
set/02
Observado
jan/04
mai/05
Previsto
out/06
fev/01
fev/02
fev/04
set/02
Observado
fev/05
jan/04
Previsto
mai/05
out/06
fev/08
Ajustado
Discrepâncias de Ajustamento:SPC
fev/06
fev/03
abr/01
Ajustado
300000
200000
fev/08
1.262.330
dez/99
151.051
100000
101.051
0
-200000
fev/04
fev/05
dez/05
dez/05
dez/03
dez/04
-48.949
-98.949
dez/01
fev/03
dez/04
dez/03
fev/02
ja
n/
m 01
ai
/0
se 1
t/0
ja 1
n/
m 02
ai
/0
se 2
t/0
ja 2
n/
m 03
ai
/0
se 3
t/ 0
ja 3
n/
0
m 4
ai
/0
se 4
t/ 0
ja 4
n/
0
m 5
ai
/0
se 5
t/ 0
ja 5
n/
0
m 6
ai
/0
se 6
t/ 0
6
dez/02
dez/01
ja
n/
m 01
ai
/0
se 1
t/0
ja 1
n/
m 02
ai
/0
se 2
t/0
ja 2
n/
m 03
ai
/0
se 3
t/0
ja 3
n/
m 04
ai
/0
se 4
t/0
ja 4
n/
m 05
ai
/0
se 5
t/0
ja 5
n/
m 06
ai
/0
se 6
t/0
6
-500000
dez/02
1.051
-300000
-400000
fev/06
fev/01
51.051
-100000
Exemplo (tabela 4.7) - Comparando Holt com Holt Winters
14
12
10
8
6
4
2
0
12
11 11
8
7
5
2
2
1
0
1
5
2
2
0
0
50
00
10 0
00
15 00
00
20 00
00
25 00
00
00
-4
50
0
-4 0 0
00
0
-3 0 0
50
0
-3 0 0
00
0
-2 0 0
50
0
-2 0 0
00
0
-1 0 0
50
0
-1 0 0
00
00
-5 0
00
00
Observações
Histograma: Holt
Histograma: Holt - Winters
17
15
15
11
10
10
5
5
1
0
1
4
3
2
0
0
0
0
15
00
0
0
50
0
00
0
12
00
0
10
00
0
75
50
0
00
0
25
00
50
00
-5
00
0
-2 0
50
00
-7
00
00
0
-1
-1
25
0
00
0
50
0
Observações
20
-1
• As discrepâncias do método
de Holt apresentaram uma
maior variabilidade em relação
ao método de Holt – Winters.
• Esta variabilidade maior das
discrepâncias é causada pela
sazonalidade dos dados que o
método Holt não captou.
Classificação mais ampla dos métodos de suavização
exponencial (equações - tabela 4.8)
Sazonalidade
Tendência
Nenhuma
Aditiva
Multiplicativa
Nenhuma
NN
NA
NM
Aditiva
AN
AA
AM
Aditiva Amortecida
AaN
AaA
AaM
Multiplicativa
MN
MA
MM
Multiplicativa Amortecida
MaN
MaA
MaM
Métodos sem tendência
NA
Previsão
Previsão
AA
Horizonte
Previsão
NM
Horizonte
Horizonte
Tabela 4.10 e 4.11
Métodos com tendência aditiva
AA
Previsão
Previsão
AN
Horizonte
Previsão
AM
Horizonte
Horizonte
Tabela 4.10 e 4.11
Métodos com tendência aditiva
amortecida
AdA
Previsão
Previsão
AdN
Horizonte
Previsão
AdM
Horizonte
Horizonte
Tabela 4.10 e 4.11
Métodos com tendência multiplicativa e
multiplicativa amortecida
MM
Previsão
Previsão
MN
Horizonte
Horizonte
MdM
Previsão
Previsão
MdN
Horizonte
Tabela 4.10 e 4.11
Horizonte
Métodos com tendência amortecida,
apresentar se tiver tempo.
• Para casos onde a tendência não é linear
• É aplicado uma constante de
amortecimento da tendência φ
• Quando fi = 0,95 por exemplo:
t = 1 amortecimento = φ1 = 0,951
t = 2 amortecimento = φ1 + φ 2 = 1,853
t = 10 amortecimento = φ1 + φ 2 + ... + φ10 = 7,654
Amortecimento φ = 1, 0,95, 0,85 para os dados de
produção de energia elétrica no Brasil (tabela 4.9)
Φ = 1 (Holt)
Ano
Φ = 0,95
Φ = 0,85
t
amortecimento
Previsão
amortecimento
Previsão
amortecimento
Previsão
2005
1
1
396.582
0,950
396.118
0,850
395.191
2006
2
2
405.854
1,853
404.486
1,573
401.890
2007
3
3
415.125
2,710
412.435
2,187
407.584
2008
4
4
424.397
3,524
419.987
2,709
412.424
2009
5
5
433.669
4,298
427.162
3,152
416.538
2010
6
6
442.940
5,033
433.977
3,529
420.035
2011
7
7
452.212
5,732
440.452
3,850
423.007
2012
8
8
461.484
6,395
446.603
4,123
425.533
2013
9
9
470.756
7,025
452.446
4,354
427.681
2014
10
10
480.027
7,624
457.998
4,551
429.506
Amortecimento φ = 1, 0,95, 0,85 para os dados de
produção de energia elétrica no Brasil (tabela 4.5) gráfico
500.000
Energia (GWh)
450.000
400.000
350.000
300.000
250.000
1995
Observado
2000
2005
fi = 1
fi = 0,95
2010
2015
fi = 0,85
Seleção automática do Métodos exponenciais exemplo com dados da venda do carro Gol 1000
• Vendas de carro de Jan/1996 a Dez/2005.
• Nº de observações: 120
35615,75
30615,75
25615,75
20615,75
15615,75
10615,75
5615,75
0
20
40
60
80
100
120
140
Seleção automática do Métodos exponenciais exemplo com dados da venda do carro Gol 1000
Tendência e sazonalidade
Método
Parâmetros
DPAM
U de Theil
AIC
1 – NA
α = 0,47 γ = 0,17
14,73
0,775
2514,602
2 – NM
α = 0,39 γ = 0,01
14,60
0,706
2520,469
3 – AA
α = 0,48 β = 0,02 γ = 0,17
15,08
0,778
2521,328
4 – AM
α = 0,43 β = 0,01 γ = 0,01
14,91
0,707
2525,526
5 – AaA
α = 0,40 β = 0,36 γ = 0,17 φ = 0,36
14,74
0,733
2520,506
6 – AaM
α = 0,32 β = 0,44 γ = 0,01 φ = 0,44
14,63
0,707
2525,862
7 – MM
α = 0,40 β = 0,01 γ = 0,01
14,70
0,710
2526,080
8 - MaM
α = 0,33 β = 0,45 γ = 0,01 φ = 0,45
14,66
0,705
2525,240
Tabela 4.14 atualizada
Conclusões
• Os métodos exponenciais obtém bons resultados para
previsões de curto prazo (1 a 4 meses), e podem ser
feitas com horizontes até o ciclo sazonal.
• Não confiar cegamente nas previsões calculadas por
um dos métodos
• Utilizar a experiência para analisar as previsões
• Sempre verificar as discrepâncias de ajustamento e as
discrepâncias de previsão.
• Se possível, recalcular as previsões a cada novo
período, as previsões com poucos passos a frente em
geral (mas não sempre) são melhores que muitos
passos.