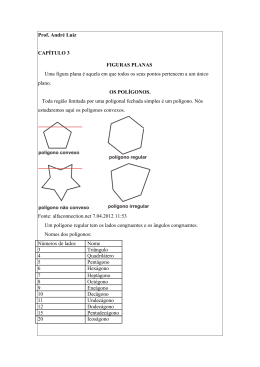
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
Geometria Plana
2a Parte
1.0 CIRCUNFERÊNCIA
1.1 Definição
Denominamos circunferência ao lugar
geométrico dos pontos do plano equidistantes
de um ponto chamado centro.
Círculo é a união da circunferência com seu
interior
Setor circular
1.2 Elementos do círculo e da
circunferência
O
C
D
E
S
Zona circular
Segmento circular
B
O
A
Coroa
circular
O: centro
AB: diâmetro da circunferência
AO = OB = OC: raio
CS: flecha
DE: corda
DCE: arco
Observação:
Observação:
1
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
2.0 Ângulos na circunferência
Ângulo central: é aquele cujo vértice
coincide com o centro de um círculo.
Ângulos excêntricos:
Interior:
A
D
A
O
O
B
C
B
Ângulo inscrito: è aquele cujo vértice
pertence a uma circunferência e seus
lados contém duas cordas.
A
O
B
Exterior:
B
Observações:
C
D
A
2
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
04. Na figura, AB é o lado de um
quadrado inscrito e BC é o lado do
decágono regular.
Qual a medida de x?
Teste de sala
01. Calcule x na figura:
x + 40º
B
C
3x + 10º
x
D
A
02. Na figura a seguir, as medidas dos
arcos AB e CD são, respectivamente,
120º e 40º. Qual o valor de ?
A
05. Determine x tendo em vista a figura a
seguir o arco BC = 120º.
C
E
B
A
80º
x
D
C
B
D
Observações:
03. Qual a medida do ângulo x, sendo AB
e AC tangentes à circunferência?
B
x
30º
A
C
3
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
3.0 Cálculos envolvendo
círculos e circunferência:
Teste de sala
01. Qual a área pintada na figura abaixo?
1o Comprimento da circunferência:
12 cm
60º
12 cm
2o Comprimento de um arco:
02. Qual a área da figura abaixo, sabendo
que o raio dos três círculos é igual a 2cm?
3o Área do círculo:
4o Área do setor:
03. Calcule a área pintada, sabendo que a
área do quadrado é igual a 16cm2.
5 o Área da coroa:
4
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
4.0 Relações métricas no
circulo (Potência de ponto)
1o - Relação das cordas
D
A
Consequências:
1 - Teorema das tangentes
B
P
P
A
B
C
2 – Teorema de Pitot: em qualquer
quadrilátero
circunscrito
a
uma
circunferência, a soma de dois lados
opostos é igual a soma dos outros dois
2o - Relação das secantes
B
A
P
C
D
3o - Relação da secante com a tangente
B
A
P
Teste de sala
T
01. Calcule os raios dos círculos inscritos
e circunscritos a um triângulo retângulo
de lados 6cm, 8cm e 10cm.
5
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
02. A menor distância do ponto P à
circunferência mede 4cm.
5.0 Quadriláteros
5.1 Definição: todo polígono convexo
que possui 4 lados.
P
5.2 Classificação:
T
Calcule o raio dessa circunferência,
sabendo que PT = 8cm.
a) Trapézio: é o quadrilátero que possui
dois lados paralelos chamados base.
Observações:
03. A figura representa os quadrados
ABCD e EFGH circunscrito e inscrito,
respectivamente, à circunferência de
centro O. Se o lado do quadrado maior
vale 6, então é correto afirmar que:
Tipos de Trapézios
Retângulo:
possui
perpendicular as bases.
A
um
lado
B
A = B = 90º
B + D = 180º
D
C
Isósceles: Possui lados não paralelos
congruentes.
(01) o lado do quadrado menor vale 4;
(02) a área do quadrado maior é o dobro
da área do quadrado menor;
(04) a razão entre a diagonal do quadrado
maior e a diagonal do quadrado
menor é um número racional;
(08) a área da parte sombreada da figura
vale 9( – 2);
(16) a área do quadrado EFGH é um
múltiplo de 3.
A
B
C
AC = BD
A=BeC=D
A + C = 180º e
B + D = 180º
D
Escaleno: lados não paralelos não são
congruentes.
A
C
B
D
AC BD
A + C = 180º e
B + D = 180º
6
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
b) Paralelogramo: Todo quadrilátero que
possui lados opostos congruentes.
Todo paralelogramo possui como
propriedades:
1 – os ângulos opostos congruentes.
2 – os lados opostos congruentes.
3 – as diagonais cortam-se no ponto
médio
4 – dois ângulos de vértices consecutivos
são suplementares.
AB = BC = CD = AD
AC
BD
Quadrado: Paralelogramo que possui os
quatro lados e os quatro ângulos
congruentes.
A
B
D
C
B
A
C
D
AB = BC = CD = AD
AB//CD e AC//BD
AC = BD e AB = CD
A=DeB=C
A + C = 180º e A + B = 180º
A = B = C = D = 90º
Daí podemos concluir que:
Tipos de Paralelogramos
Quadriláteros
Retângulo: paralelogramo com os quatro
ângulos internos retos e as diagonais
congruentes.
A
B
T
R
Q
L
D
C
A = B = C = D = 90º
e
AD = BC
Losangos: Paralelogramo que possui os
quatro lados congruentes, suas diagonais
se cruzam perpendicularmente e coincide
com as bissetrizes dos vértices.
B
A
P
M
T – Trapézio
P – Paralelogramo
R – Retângulo
L – Losango
Q – Quadrado
C
D
7
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
6.0 Polígonos
Polígono é a reunião de uma linha
fechada simples, formada apenas por
segmentos de retas, com a sua região
interna.
6.1 Elementos do polígono.
Obs.: Os demais polígonos não possuem
nomes em especial. São tratados como,
por exemplo, polígono de 17 lados, 13
lados, 22 lados e assim por diante.
6.3 Soma dos ângulos internos
Si =
B
Demonstração:
A
C
ai
E
ae
D
A: vértice
AB: lado
ai: ângulo interno
ae: ângulo externo
BE: diagonal
6.4 Soma dos ângulos externos
6.2 Nomenclatura
Demonstração:
no de lados
Se = 360º
nome do polígono
3
Triângulo
4
Quadrilátero
5
Pentágono
6
Hexágono
7
Heptágono
8
Octógono
9
Eneágono
10
Decágono
11
Undecágono
12
Dodecágono
15
Pentadecágono
20
Icoságono
6.5 Polígonos Regulares
È todo polígono que possui ângulos e
lados congruentes.
Daí, podemos calcular cada ângulo
interno e externo do polígono, se ele for
regular.
6.5.1 Ângulo interno
ai =
.
6.5.2 Ângulo externo
ae =
.
8
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
6.6 Número de diagonais
d=
4.0 Aumentando-se o número de lados de
um polígono em 3 unidades, seu número
de diagonais aumenta em 21 unidades.
Determine o número de diagonais desse
polígono.
Demonstração:
7.0 Polígonos inscritos e
circunscritos
Observação:
a) Triângulo equilátero
L 3
2
h
r=
3
2h
R=
3
h=
R
r
Teste de sala
01. Qual o polígono cuja soma dos
ângulos internos vale 1800º?
b) Quadrado
R
r
02. Determine o polígono cujo número de
diagonais é o triplo do número de lados.
d= L 2
L 2
R=
2
L
r=
2
c) Hexágono
03. Determine o número de diagonais de
um polígono regular convexo cujo ângulo
externo vale 24º.
R
R=L
L 3
r=
2
r
9
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
8.0 Resumo das áreas de
figuras planas.
Teste de Sala (1a parte)
Q.01
Na figura abaixo, tem-se uma argola
circular apoiada no ponto A, situado num
plano horizontal.
A
B
Pretende-se girar a argola de modo que
ela rode em linha reta sobre o plano até
atingir o ponto B, distante 50,24cm de A.
Se o diâmetro externo da argola é de 4cm,
qual o número de voltas completas que
ela dará até que atinja o ponto B?
a) 2
b) 3
c) 4
d) 5
e) 6
Q.02
Considere um trapézio isósceles ABCD,
representado na figura abaixo.
A
D
B
C
Se AB = 8cm e CD = 12cm, então a área
do trapézio, em centímetros quadrados,
pode ser dado pela expressão:
a)
b)
c)
d)
e)
18 cos
18 sen
20 cos
20 tg
24 tg
10
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
c) 10 cm
d) 10 2 cm
e) 10 3 cm
Q.03
B
A
Q.05
Na
figura
abaixo
tem-se
uma
circunferência da centro O e diâmetro
AB de medida 8cm; Os arcos AO e OB
são semicircunferências.
A área da região sombreada, em
centímetros quadrados, é:
C
Na circunferência, figura acima, o raio
mede 3cm e AC = 3cm.
O seno da ângulo ABC é:
a) 1
1
b)
2
A
a)
b)
c)
d)
e)
1
2
3
d)
2
2
e)
2
c) -
O
B
12
8
6
4
2
Q.06
Na figura abaixo, AB = 16cm, EC =
15cm, DF = 6cm.
Q.04
Na figura tem-se um triângulo equilátero
ABC sobre cujos lados foram construídos
quadrados.
E
D
A
B
B
A
C
F
A medida de BD, em centímetros, é:
D
C
E
Se o lado do triangulo mede 10cm, qual é
a distância de D a E?
a) 5 2 cm
b) 5 3 cm
a) 15
b) 13,5
c) 12
d) 10,5
e) 9
11
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
Q.07
Do alto de uma torre AP, um observador
avista os trechos AX e XB de uma estrada
horizontal e retilínea sob ângulos de 30º,
conforme ilustração.
de modo que o perímetro da figura
colorida seja igual a 3 , é
2
a) + 1
b) 1
c) 2
d) + 2
P
30º 30º
A
B
X
Se a altura da torre é 15 3 m
comprimento do trecho XP, em metros, é:
a) 30
b) 25 3
c) 30 3
d) 52
e) 40 3
Q.10
A roda de uma bicicleta tem 90cm de
diâmetro.
Então,
a
distância
percorrida por um ciclista nessa
bicicleta em movimento, quando a
roda dá 2.000 voltas completas sem
deslizar:
Considere
a)
b)
c)
d)
3,14
é inferior a 3 quilômetros.
está entre 3 e 4 quilômetros.
está entre 4 e 5 quilômetros.
é superior a 5 quilômetros.
Q.08
Q.11
Calcule
o
comprimento
da
circunferência inscrita em um
triângulo retângulo de catetos
medindo 4cm e 3cm.
A área, em m3, da região pintada é:
Q.12
Nesta figura, estão representadas três
circunferências, tangentes duas a
duas, e uma reta tangente às três
circunferências:
a)
b)
c)
d)
e)
64 - 24 3
48 - 9 3
32 - 27 3
16 - 9 3
8 -2 3
Q.09
Na figura abaixo, estão indicados um
retângulo ABCD e um semicírculo de
centro E. Nessas condições, é
CORRETO afirmar que o valor de L,
Sabe-se que o raio de cada uma das
duas circunferências maiores mede 1
cm.
12
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
Então, é CORRETO afirmar que a
medida do raio da circunferência
menor é
a) 1 cm
b)
3
1
cm
4
c)
2
cm
2
d)
2
cm
4
Q.13
Num triângulo retângulo, a medida da
hipotenusa é o triplo da medida de um
dos catetos.
A razão entre a medida da hipotenusa
e a medida do outro cateto é igual a:
Q.15
A área e o perímetro de um triângulo
retângulo cuja hipotenusa mede 10
cm e um dos catetos 6 cm são,
respectivamente:
a) 48cm2 e 24cm.
b) 30cm2 e 15cm.
c) 24cm2 e 24cm.
d) 60cm2 e 60cm.
e) 6cm2 e 12cm.
Q.16
Na figura abaixo, ABD e BCD são
triângulos retângulos isósceles. Se
AD = 4, qual é o comprimento de
DC?
3
a)
22
3
b)
3 2
4
3
22
c)
3
d)
2
12
e) 9
Q.14
Na figura abaixo, todos os triângulos
são retângulos isósceles, e ABCD é
um quadrado.
a) 4
b) 6
c) 7
d) 8
e) 8
2
2
Q.17
Na figura abaixo tem-se um trapézio,
com as medidas dos lados dadas em
centímetros.
10
13
15
24
Nessas
quociente
condições,
GH
CE
.
determine
o
A altura desse trapézio,
centímetros, é igual a
a) 12
b) 11
c) 10
d) 9
e) 8
em
13
VESTIBULAR
MATEMÁTICA E SUAS TECNOLOGIAS
Módulo III
VILAS
A
Q.18
A figura representa três semicírculos,
mutuamente tangentes dois a dois, de
diâmetros AD, AC e CD .
B
E
F
D
Sendo CB perpendicular a AD , e
sabendo-se que AB 4cm e DB 3cm , a
medida da área da região sombreada
na figura, em cm2, é igual a
a) 1,21 .
b) 1,25 .
c) 1,36 .
d) 1,44 .
e) 1,69 .
a)
b)
c)
d)
e)
C
72°
54°
60°
76°
36°
Q.19
Na figura, o raio
da
OA
circunferência mede 6cm. Adotandose
3 , a área da região sombreada,
em cm2, é igual a
a)
b)
c)
d)
e)
9(4
9
3)
3
4 3
9 3
4(9
3)
Q.20
Na figura, ABCDE é um pentágono
regular, EF é paralelo a AB e BF é
paralelo a AE . A medida do ângulo
é
14