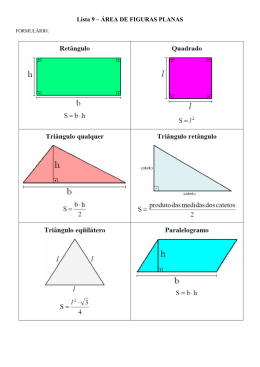
MATÉRIA: Matemática
PROFESSOR: Vinícius
SÉRIE: 2º ano
TIPO: Roteiro e trabalho de Recuperação - 2ª etapa
ROTEIRO:

ÁREAS
QUESTÃO 01
Uma casa ocupa a quarta parte de um terreno, como nos mostra a figura a seguir. O restante do terreno é usado como
quintal. Para cobrir o quintal com certo piso, compraram-se caixas com 1,5 m2 de piso cada uma.
Quantas caixas foram compradas?
a) 300
b) 200
c) 400
d) 250
QUESTÃO 02
A diagonal AC do quadrado ABCD mede 2 cm. Se o diâmetro de cada uma das semicircunferências na figura abaixo
é igual à metade do lado do quadrado, calcule a área da região assinalada.
QUESTÃO 03
Em matemática, verifica-se em várias situações uma correspondência entre um modelo algébrico e um modelo
geométrico. Como exemplo, observe a figura a seguir:
A área da figura acima corresponde à:
a) a  b 
2
b) a 2  2ab  b 2
c) a 2  b 2
d) a  b
. a  b
QUESTÃO 04
Um terreno de forma retangular foi dividido em quatro lotes retangulares onde são conhecidas as áreas de três deles,
como ilustra a figura abaixo. Qual é a área total do terreno, em m2?
A) 55,6
B) 56,6
C) 57,6
D) 58,6
QUESTÃO 05
Um terreno de 72 m2 de área é formado por 8 quadrados congruentes, conforme mostra a figura abaixo, quanto mede a
cerca que delimita o terreno (perímetro da figura)?
QUESTÃO 06
O apótema do triângulo eqüilátero inscrito no círculo abaixo mede 2 3 cm. Determine a área da região colorida.
QUESTÃO 07
Determine a medida x, indicada na figura abaixo, de modo que a soma das áreas dos retângulos coloridos seja 288 cm2.
QUESTÃO 08
Num triângulo eqüilátero de lado 10 cm, inscreve-se um quadrado, conforme a figura seguinte. A área hachurada, em
cm2, vale:
A) 25 3 
300
C) 25 3 
(2  3 ) 2
B) 150 3 
300
(2  3 )
2
225
(2  3 ) 2
D) 150 3 
225
(2  3 ) 2
QUESTÃO 09
Na figura a seguir, o triângulo ABC é retângulo em B. O ângulo em C mede 60º
e, ainda, CE  CD  FA  x . Sabendo-se que BC  1 e que a soma das
áreas dos triângulos CED e EBF é igual a área do quadrilátero DEFA, qual deve
ser, então, o valor de x?
a) 2 3  3
b) 3 3  2
c)
32
d)
3 3
QUESTÃO 10
A altura do trapézio é 4; então, a diferença entre as áreas dos triângulos assinalados é:
a) 1
b) 2
c) 3
d) 4