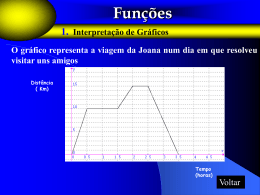
Generalidades sobre
funções
Matemática A – 10º Ano
Tema II
Porto Editora - NetProf
Noção de função
A
Uma função é uma
relação unívoca entre
dois conjuntos, A e B,
isto é, a cada elemento
de A corresponde um e
um só elemento de B.
B
f
C
xA 1 y B : y=f(x)
A chama-se Domínio da função  Df
Os elementos de A chamam-se Objectos
B chama-se Conjunto de chegada da função
C chama-se Contradomínio da função  D’f
Os elementos de C chamam-se Imagens
Porto Editora - NetProf
Função real de variável
real
Seja f uma função.
Se o domínio de f é um subconjunto de
IR (A) e o conjunto de chegada é IR,
então f diz-se uma função real de
variável real.
f : A  IR  IR
x  y  f ( x)
Porto Editora - NetProf
Função: sim ou não?
Por exemplo
Porto Editora - NetProf
Função: sim ou não?
Porto Editora - NetProf
Estudo de uma função:
Domínio
Domínio de uma função, real de variável
real, é o conjunto dos números reais
para os quais têm significado as
operações na expressão algébrica que
a define.
Porto Editora - NetProf
Df   ,4   4,2  2,
Porto Editora - NetProf
Estudo de uma função:
Contradomínio
Contradomínio de uma função, real de
variável real, é o conjunto de todos os
números reais que são imagens de
algum elemento do domínio (objecto).
Df  y  IR : x  Df : y  f x
Porto Editora - NetProf
Df   ;7
Porto Editora - NetProf
Estudo de uma função:
Zeros e Sinal
Zero de uma função é
um objecto (x) cuja
imagem é nula.
x  Df : f x   0
Uma função diz-se positiva, quando a sua
imagem é positiva: f(x) > 0
Uma função diz-se negativa, quando a sua
imagem é negativa: f(x) < 0
Porto Editora - NetProf
Função Positiva:
x  ]-8,-4[  ]-4,2[  ]4,6[
Zeros: -8 e 6
Função Negativa:
x  ]-,-8[  ]2,4]  ]6,+ [
Porto Editora - NetProf
Estudo de uma função:
Monotonia e extremos
• Função crescente
• Máximo Absoluto - max
– em sentido lato
x1,x2Df : x1x2  f(x1)f(x2)
– em sentido estrito
x1,x2Df : x1>x2  f(x1)>f(x2)
• Função decrescente
– em sentido lato
x1,x2Df : x1x2  f(x1)f(x2)
– em sentido estrito
x1,x2Df : x1>x2  f(x1)<f(x2)
– xDf,f(x)  max
• Mínimo Absoluto - min
– xDf,f(x)  min
• Máximo Relativo - maxr
– I Df xI,f(x)  maxr
• Mínimo Relativo - minr
– I Df xI,f(x)  minr
Porto Editora - NetProf
Máximos Locais: 2; 2,5; 7
Maximizantes: ]-4,2[; 5; -6
Máximo Absoluto: 7
Mínimos Locais: -4, 2
Minimizantes: 3; ]-4,2[
Função crescente para:
x  ]-∞,-6] e x  [3,5]
Função decrescente para:
x  [-6,-4[, x  ]2,3]
e x  [5,+∞ [
Função Constante para:
x  ]-4,2[
Porto Editora - NetProf
Estudo de uma função:
Paridade
• Uma função f, real de variável real,
diz-se par se e só se:
xDf: f(-x) = f(x)
• Uma função f, real de variável real,
diz-se ímpar se e só se:
xDf: f(-x) = -f(x)
Porto Editora - NetProf
Simetria em relação ao eixo dos yy`s
Porto Editora - NetProf
Simetria em relação à origem
Porto Editora - NetProf
Estudo de uma função:
Injectividade
• Uma função f, real de variável real,
diz-se injectiva se e só se:
x1, x2Df : x1 ≠ x2 f(x1) ≠ f(x2)
ou, de forma equivalente:
x1, x2Df : f(x1) = f(x2)  x1 = x2
Porto Editora - NetProf
Função Injectiva:
sim ou não?
Porto Editora - NetProf
Função Injectiva:
sim ou não?
Por exemplo
Porto Editora - NetProf