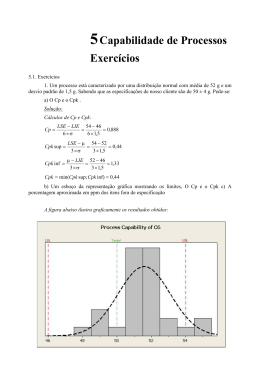
Carta de controle para o desvio-padrão
9
O desvio padrão é um indicador mais eficiente da
variabilidade, principalmente para amostras grandes
(a amplitude perde eficiência).
Recomenda-se o uso da carta Xb - S quando:
Os dados forem coletados por computador e for
fácil de implementar uma rotina de cálculo
„ Processos sofisticados, controlados por
especialistas
„ Amostras grandes (subgrupos > 10 )
„
Cálculo dos limites de controle
9
A fórmula para o cálculo do desvio padrão é:
9
Os limites de controle são calculados usando:
Para o desvio padrão:
LCS = x + A3 S
Para a média:
n
B4
B3
A3
2
3,27
0
2,66
LCS = B4 S
LCI = B3 S
LCI = x − A3 S
3
2,57
0
1,95
4
2,27
0
1,63
5
2,09
0
1,43
6
1,97
0,03
1,29
8
1,82
0,19
1,10
10
1,72
0,28
0,98
15
1,57
0,43
0,79
20
1,49
0,51
0,68
Cartas de controle para X e S
Ex.: Dez amostras, cada uma contendo 5 medidas do diâmetro de
roscas produzidas por uma industria de autopeças, foram coletadas
da produção. Construa uma carta de controle para média e desvio
padrão.
A m o s tra
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
7 .1
7 .1
7 .1 2
7 .1 1 5
7 .0 9
7 .1 1
7 .1 0 5
7 .1
7 .0 6 5
7 .1 2 5
7 .1 0 5
7 .1
7 .1 1 5
7 .0 9 5
7 .1 1
7 .0 7
7 .0 9
7 .1
7 .0 8
7 .1
7 .0 9 5
7 .1 0 5
7 .1
7 .1
7 .1 2
2
7 .0 9 5
7 .1
7 .1 0 5
7 .1 2
7 .0 9 5
7 .1
7 .0 9 5
7 .1 1 5
7 .0 9
7 .1 3
7 .1
7 .1 1
7 .0 9
7 .0 9
7 .0 7
7 .0 7 5
7 .1 3
7 .1
7 .0 7
7 .1 1
7 .1 0 5
7 .0 7
7 .1
7 .1 0 5
7 .1 1 5
3
7 .1
7 .0 9 5
7 .1
7 .1 1 5
7 .1 1
7 .1 0 5
7 .1
7 .0 9 5
7 .1 1
7 .0 9 5
7 .1 1 5
7 .0 8 5
7 .0 8 5
7 .0 9 5
7 .0 9 5
7 .0 8
7 .1
7 .0 9
7 .0 9
7 .0 7
7 .0 9 5
7 .1 1
7 .1 0 5
7 .1 0 5
7 .1 1
4
7 .1 0 5
7 .1 0 5
7 .1 2
7 .1 1 5
7 .1 2
7 .1
7 .1 0 5
7 .1 0 5
7 .1 0 5
7 .1
7 .0 9 5
7 .0 9
7 .0 9
7 .1
7 .1
7 .1
7 .1 1
7 .0 9 5
7 .1 1
7 .1 1
7 .0 9 5
7 .1 1
7 .1 1
7 .1 1
7 .1 3
5
7 .1 0 5
7 .1
7 .1
7 .1 2
7 .1 0 5
7 .1
7 .0 8 5
7 .1 2 5
7 .1 0 5
7 .1 1 5
7 .0 7 5
7 .0 8
7 .1 1
7 .0 8
7 .1 1
7 .0 9
7 .1
7 .0 8
7 .1
7 .1 1
7 .1
7 .1 1
7 .1 0 5
7 .0 8
7 .1 1 5
M é d ia
7 .1 0 1
7 .1
7 .1 0 9
7 .1 1 7
7 .1 0 4
7 .1 0 3
7 .0 9 8
7 .1 0 8
7 .0 9 5
7 .1 1 3
7 .0 9 8
7 .0 9 3
7 .0 9 8
7 .0 9 2
7 .0 9 7
7 .0 8 3
7 .1 0 6
7 .0 9 3
7 .0 9
7 .1
7 .0 9 8
7 .1 0 1
7 .1 0 4
7 .1
7 .1 1 8
7 .1 0 0 8
D e s v io
0 .0 0 4 2
0 .0 0 3 5
0 .0 1 0 2
0 .0 0 2 7
0 .0 1 1 9
0 .0 0 4 5
0 .0 0 8 4
0 .0 1 2 0
0 .0 1 8 4
0 .0 1 5 2
0 .0 1 4 8
0 .0 1 2 0
0 .0 1 3 5
0 .0 0 7 6
0 .0 1 6 4
0 .0 1 2 0
0 .0 1 5 2
0 .0 0 8 4
0 .0 1 5 8
0 .0 1 7 3
0 .0 0 4 5
0 .0 1 7 5
0 .0 0 4 2
0 .0 1 1 7
0 .0 0 7 6
0 .0 1 0 8
Cartas de controle para Média
Amostras
Carta - Média
7.13
7.12
7.11
7.1
7.09
7.08
7.07
7.06
LSC - 7.1161
LM - 7.1008
LIC - 7.0853
Medidas
1
3
5
7 9 11 13 15 17 19 21 23 25
Medidas
Carta para Desvio Padrão
Carta Desvio Padrão
0.025
Medidas
0.02
LSC - 0.0225
LM - 0.0108
LIC - 0
Medidas
0.015
0.01
0.005
0
1 3 5 7 9 11 13 15 17 19 21 23 25
Amostras
Avaliação da Estabilidade e da
Capacidade do Processo
A condição de controle
Processo estável ou sob controle:
Quando as características da qualidade de um produto
exibem apenas variação devido a causas comuns.
Processo fora de controle:
9Os pontos caem fora dos limites de controle;
9Os pontos apresentam alguma configuração especial.
Zonas do Gráfico de Controle
3σ
LCS
linha
central
LCI
Zona C (+ 3 sigma)
C = 2,14 %
2σ
Zona B (+ 2 sigma)
B = 13,60 %
1σ_
Zona A (+ 1 sigma)
A = 34,13 %
Zona A (- 1 sigma)
A = 34,13 %
1σ
Zona B (- 2 sigma)
B = 13,60 %
2σ
Zona C (- 3 sigma)
C = 2,14 %
S, etc.
3σ
Processo Fora de Controle
Condição 1. Pontos fora de limites de controle
LCS
3σ
2σ
linha
central
1σ_
S, etc.
1σ
2σ
LCI
3σ
Processo Fora de Controle
Condição 2. Duas em três em seqüência além de dois desvios
padrão, em um lado da linha central.
LCS
3σ
2σ
linha
central
1σ_
S, etc.
1σ
2σ
LCI
3σ
Processo Fora de Controle
Condição 3. Quatro sobre cinco em seqüência além de um
desvio padrão em um lado da linha central.
LCS
3σ
2σ
linha
central
1σ_
S, etc.
1σ
2σ
LCI
3σ
Processo Fora de Controle
Condição 4. Seqüência significativa de pontos em ambos
os lados da linha central. Em geral, sete ou oito pontos em
seqüência.
LCS
3σ
2σ
linha
central
1σ_
S, etc.
1σ
2σ
LCI
3σ
Processo Fora de Controle
Ocorrência de ciclos
Avaliando a Capacidade do Processo
9 Após a avaliação da estabilidade do processo é
importante realizarmos estudos para avaliarmos a
capacidade do processo.
9 É possível que mesmo um processo com variabilidade
controlada e previsível produza itens defeituosos
9Somente processos estáveis devem ter sua capacidade
avaliada
Capacidade do Processo
9 Capacidade é a habilidade do processo em produzir
produtos dentro dos limites de especificação.
9 Utilizam-se técnicas estatísticas, a fim de estudar a
variabilidade do processo, comparando-a com as
especificações (tolerâncias).
9 Os principais índices utilizados para obter a capacidade
do processo são o Cp e o Cpk.
Índices de capacidade
Os índices de capacidade processam as informações de
forma que seja possível avaliar se um processo é capaz de
gerar produtos que atendam às especificações provenientes
dos clientes internos e externos.
Para usar os índices de capacidade é necessário que :
9 o processo esteja sobre controle estatístico
9 a variável de interesse tenha distribuição próxima da
normal
Índices de capacidade
Cp: índice de capacidade potencial do processo. Leva em
consideração a dispersão do processo (curto prazo) em
relação aos limites de especificação.
Cp =
LSE − LIE
^
6σ
−
R/ d 2
O índice relaciona aquilo que se deseja produzir (LSE LIE = variabilidade permitida ao processo) com a
variabilidade natural do processo (6σ)
Índices de capacidade
Cpk: índice de capacidade nominal do processo. Leva em
consideração a dispersão do processo (curto prazo) e
centragem do processo em relação aos limites de
especificação.

=
=
 LSE − X X − LIE
Cpk = min 
'
^
^
 3σ −
3σ −
R/ d 2
R / d2






O índice Cpk pode ser interpretado como uma
medida da capacidade real do processo.
Índices Cp e Cpk
9 O índice Cpk é menor que o índice Cp quando o
processo está descentrado e é igual ao Cp quando o
processo está centrado;
9 O índice Cpk, que mede a capacidade real do
processo, é sempre menor ou igual ao índice Cp que
mede a máxima capacidade do processo quando ele está
centrado.
Índices de Capacidade Potencial do Processo
(Cp)
LIE
-6 σ -5 σ -4 σ
LSE
-3 σ
-2 σ
µ
-1 σ
+1 σ
+2 σ
Diferença entre os limites
6 desvios (3 para cada lado)
Cp
=
− LIE
LSE
^
6 σ
−
R / d
2
+3 σ
+4 σ +5 σ
+6 σ
Índices de Capacidade Nominal do Processo
(Cpk)
LIE
LSE
µ
-6 σ -5 σ -4 σ
-3 σ
-2 σ
-1 σ
Alvo
+1 σ
+2 σ
+3 σ
+4 σ +5 σ
+5 σ
Diferença entre média e LIE


=
=
 LSE − X X − LIE 
Cpk = min 
'

^
^
 3σ −
3σ − 
/
R
d
R / d2 
2

Diferença entre LSE e a média
3 desvios
3 desvios
Avaliação gráfica da capacidade de
processos
9 Consiste na comparação de histogramas e/ou gráfico
construídos para as características da qualidade de interesse
com os limites de especificação.
Um processo pode não ser capaz por apresentar:
9 Elevada variabilidade
9 Média deslocada em relação ao ponto médio dos limites
de especificação
Avaliação gráfica da capacidade de
processos
Processo capaz e não capaz
0.06
0.06
0.05
0.05
0.04
0.04
f(x)
f(x)
Processo descentrado x centrado
0.03
0.03
0.02
0.02
0.01
0.01
0.00
30
40
50
60
70
80
90
100
x: Título
Limites de Especificação
Alvo
Distribuição de 'titulo'
0.00
30
40
50
60
70
80
90
x: Título
Limites de Especificação
Alvo
Distribuição de 'titulo'
Processo descentrado Cpk < Cp Processo centrado Cpk = Cp
Fig. adaptada de RIBEIRO, José L. D., TEM CATEN, Carla. Controle Estatístico do Processo. Série monográfica Qualidade.
PPGEP-UFRGS, 2001.
Índices de Desempenho
Pp: índice de desempenho potencial do processo. Leva em
consideração a dispersão do processo em relação aos
limites de especificação.
LSE − LIE
Pp =
^
6σ S
Ppk: índice de desempenho nominal do processo. Leva em
consideração a dispersão e centragem do processo em
relação aos limites de especificação.
=
=

 LSE − X X − LIE
'
Cpk = min 
^
^

3σ S
3σ S




Classificação do processo com respeito
a sua capacidade
Itens fora das especificações
Especificação bilateral e
Porcesso não centrado e/ou
processo centrado (ICP
especificaçào unilateral (ICP
apropriado:
apropriado: Cpk)
Cp=Cpk
Classificação
Valor de Cpk
Capaz
Razoavelmente
capaz
Incapaz
> ou = 1,33
70
35
1< ou = Cpk < ou = 1,33
Entre 70 e 2700
Entre 35 e 1350
<1
mais de 2700
mais de 1350
Relacionamento entre Cp e Cpk e
Nível Sigma
Nível Sigma
Cp
Cpk
Ppm
± 1σ
± 2σ
± 3σ
± 4σ
± 5σ
± 6σ
0,33
0,67
1,00
1,33
1,67
2,00
0,33
0,67
1,00
1,33
1,67
2,00
317.311
45.500
2.700
63
0,57
0,002
Diferenciar Longo Prazo e Curto Prazo
A curto prazo, o desvio padrão é estimado
usando a média das amplitudes parciais
dividido pela constante d2 que varia de
acordo com o tamanho da amostra
Tamanho da
amostra
2
3
4
5
6
Valor
1,128
1,693
2,059
2,326
2,543
Tamanho da
amostra
7
8
9
10
A longo prazo, o desvio padrão
é estimado pela fórmula usual:
Valor
^
−
σ R/d
−
2
2,704
2,847
2,970
3,078
^
σS =
∑(x − x)
2
i
n −1
R
=
d2
Capacidade do Processo no MINITAB
P ro ce sso C ap acid ad e - G radu ação Alco ó lica (°G L )
LIE
LS E
Within
O ver all
Pr oces s D ata
39,8
LSL
T ar g et
*
U SL
Sample M ean
40,2
40,0106
Sample N
109
StD ev( Within)
0,0857795
StD ev( O ver all)
0,103616
Potential ( W ithin) C apability
Cp
0.78
C PL
0.82
C PU
0.74
C pk
0.74
O ver all C apability
3 9 .8
3 9 .9
4 0 .0
O bser ved Per for manc e
PPM < LSL
0.00
PPM > U SL
9174.31
PPM T otal
9174.31
4 0 .1
4 0 .2
4 0 .3
Exp. Within Per for mance
PPM < LSL
7052.96
PPM > U SL
PPM T otal
13602.47
20655.42
4 0 .4
4 0 .5
Exp. O ver all Per for mance
PPM < LSL
21075.70
PPM > U SL
33746.47
PPM T otal
54822.18
Pp
0.64
PPL
PPU
0.68
0.61
Ppk
0.61
C pm
*