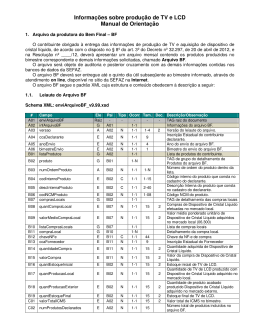
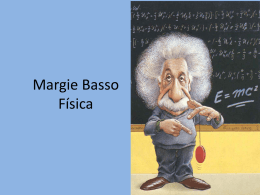Uma armação apresenta um formato retangular de lados a e b, sendo o
lado a duas vezes maior do que o lado b, conforme a figura abaixo. Os
coeficientes de dilatação linear dos lados a e b são iguais a αa e αb,
respectivamente. Ao longo da diagonal da armação retangular, é fixada
uma barra de comprimento x feita de um certo material, com coeficiente de dilatação linear αx.
Determine o coeficiente de dilatação linear α em função dos coeficienx
tes de dilatação αa e αb, de forma que a barra não fique nem tensionada
e nem comprimida, devido às variações de temperatura.
RESOLUÇÃO:
∆x 2 = ∆a2 + ∆b 2
x02 αx2 ∆θ2 = a02 αA2 ∆θ2 + b02 αB2 ∆θ2
Sabendo que:
a0 = 2b0
e
x 0 2 = a0 2 + b0 2
x02 = (2b0)2 + b02
x02 = 4b02 + b02 ⇒ x02 = 5b02
Assim:
5b02 αx2 = (2b0)2 αA2 + b02 αB2
5b02 αx2 = 4b02 αA2 + b02 αB2
5αx2 = 4αA2 + αB2
∆a
∆x
αx =
4α A 2 + α B 2
5
∆b
∆b
∆a