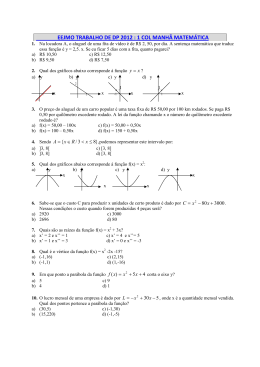
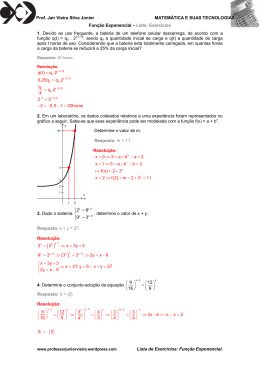
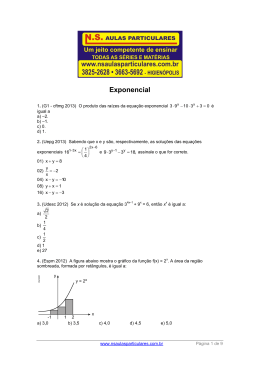
Tópico 2. Funções elementares
2.1 Função constante
Dado um número real k, chama-se função constante a função f :    , definida por
f(x) = k.
Exemplos
a) f(x) = 1
b) f(x) = -3
c) f(x) = 2
d) f(x) =
5
3
Gráfico da função constante
O gráfico da função constante f(x) = k é uma reta paralela ao eixo x passando pelos pontos
de ordenada y = k. Nos exemplos (a) e (b) acima temos:
2.2 Função polinomial do 1º grau
Dados os números reais a e b, com a  0, chama-se função do 1º grau a função f :   
, definida por y = ax + b ou f(x) = ax + b.
O número a é chamado coeficiente angular e o número b é chamado coeficiente linear
(onde a reta corta o eixo y).
Exemplos:
a) f(x) = 5x-2
coeficiente angular: ___
coeficiente linear: ___
b) y = x + 3
coeficiente angular: ___
coeficiente linear: ___
coeficiente angular: ___
coeficiente linear: ___
c) g(x)= 
x
2
Observação: f ( x )  x é chamada Função Identidade.
Gráfico da função polinomial do 1ºgrau
O gráfico de uma função do 1º grau é uma reta não paralela nem ao eixo x, nem ao eixo y.
Seu domínio é o conjunto dos números reais e sua imagem também é o conjunto dos números reais.
Ou seja, Dom f=  e Im f =  .
Exemplos:
1) Construa o gráfico das seguintes funções:
a) Y = 2x+3
b) y = -2x+3
2) Escreva a função correspondente ao gráfico:
2.3 Função polinomial do 2º grau
Dados os números reais a e b, com a  0, chama-se função polinomial de 2º grau ou função
quadrática a função f :    , definida por y = ax2 + bx + c ou f(x) = ax2 + bx + c.
2
Exemplos:
a) f(x) = x2 – 4x – 3
a = ____ b =____ c =____
b) y = x2 – 9
a = ____ b =____ c =____
c) g(x) = – 4x2 + 2x – 3
a = ____ b =____ c =____
2
a = ____ b =____ c =____
d) h(x) = x + 7x
Exercício: Sendo f(x) = (m + 5)x2 + 2x – 4, determine m de modo que:
a)
f(x) seja do 2º grau
b)
f(x) seja do 1º grau
Gráfico da função quadrática
O gráfico de uma função do 2º grau é uma curva denominada parábola. Seu domínio é o
conjunto dos números reais e sua imagem é um subconjunto dos números reais. Ou seja, Dom f= 
e Im f   .
Exemplos:
Construa o gráfico das seguintes funções:
b) f(x) = x2
b) g(x) = – x2
 Concavidade
O sinal de a (coeficiente de x2) determina a concavidade da parábola. Assim:
 Se a > 0 (a positivo), a concavidade é voltada para cima: 
 Se a < 0 (a negativo), a concavidade é voltada para baixo: 
Podemos verificar isto nos exemplos anteriores, onde f(x) tem concavidade voltada para
cima, pois a = 1 e g(x) tem concavidade voltada para baixo, pois a = – 1.
 Zeros (ou raízes) de uma função do 2º grau
Denominam-se zeros ou raízes de uma função quadrática os valores de x que anulam a
função, ou seja, que tornam f(x) = 0. Em termos de representação gráfica, são as abscissas dos pontos
onde a parábola corta o eixo x.
3
Denomina-se equação do 2º grau com uma variável toda equação da forma ax2 + bx + c = 0
, onde x é a variável e a, b, c   com a  0.
Observação: c é a ordenada do ponto (0, c), onde a parábola corta o eixo y.
Exemplos:
a) 2x2 – 3x + 1 = 0
a = 2; b = -3;
c=1
b) x2 – 4 = 0
a = 1; b = 0;
c = -4
c) y2 + 3y = 0
a = 1; b = 3;
c=0
d) 5x2 = 0
a = 5;
c=0
b = 0;
Resolução da equação do 2º grau
Resolver uma equação significa determinar o conjunto solução (ou conjunto verdade) dessa
equação. Para a resolução das equações do 2º grau, utilizamos a Fórmula Resolutiva ou Fórmula de
Bhaskara (século XII) dada abaixo:
Se ax2 + bx + c = 0 e a  0, então
, onde
  0
 Se   0 a equação tem raízes reais 
  0
 Se   0 a equação não tem raízes reais.
Exemplos: Dada a função f, calcular os zeros desta função.
a) f(x) = 2x2 – 3x + 1
b) h(x) = x2 – 4
c) g(x) = x2 + 3x
d) y = 5x2
e) g(x) = x2 – 5x + 7
f) y = x2 – 6x + 9
Forma fatorada da equação do 2º grau
𝑦 = 𝑎(𝑥 − 𝑥1 )(𝑥 − 𝑥2 )
onde x1 e x2 são as raízes da equação.
4
Vértice da Parábola
Toda parábola tem um ponto de ordenada máxima ou um ponto de ordenada mínima. A esse
ponto chamaremos vértice da parábola e o representaremos por V(xv,yv) onde
xv  
b
2a
e
yv  

4a
Assim:
Exemplos
1) Determine as coordenadas do vértice V da parábola que representa a função
f ( x )  x 2  3x  2
2) Determine a e b de modo que o gráfico da função definida por y  ax 2  bx  9 tenha
o vértice no ponto (4,-25).
Valor máximo e valor mínimo da função do 2º grau
Examinando os gráficos abaixo, observa-se que:
Se a > 0,
mínimo da função.
é o valor
Se a < 0,
é o valor
máximo da função.
5
Exercício:
1)
A função f(x) = x2 – x – 6 admite valor máximo ou valor mínimo? Qual é esse valor?
2.4 Função exponencial
Dado um número real a, tal que a  1 e a > 0, é dado o nome de função exponencial de base
a à função f :    definida por y = ax ou f(x) = ax .
Exemplos:
a) f(x) = 2x
 
x
b) f(x) = 2
c) f(x) = (0,4)x
 1
d) f(x) =  
3
e) f(x)= e x
x
Gráfico da função exponencial
O gráfico de uma função exponencial é uma curva, em que devem ser observadas algumas
particularidades:
 o gráfico nunca corta o eixo das abscissas (Ox), ou seja, a função não tem zeros (raízes);
 o gráfico corta o eixo das ordenadas (Oy) no ponto (0,1);
 os valores de y são sempre positivos.
Seu domínio é o conjunto dos números reais e sua imagem é o conjunto dos números reais
positivos. Ou seja, Dom f =  e
Im f =
 = ]0; +[.
*

Quanto à base da função, devemos considerar dois casos:
 Base maior que um (a > 1)
f (x) = ax ( a > 1 )
 A função é crescente.
 Dom f =  .
 Sua imagem são os reais positivos, Im =
 = ]0; +[.
*

 Para quaisquer x1 e x2 do domínio: x2 > x1  y2 > y1.
6
 Base entre zero e um (0 < a < 1)
f (x) = ax ( 0 < a < 1 )
 A função é decrescente.
 Dom f =  .
 Sua imagem são os reais positivos, Im =
 = ]0; +[.
*

 Para quaisquer x1 e x2 do domínio: x2 > x1  y2 < y1.
As funções exponenciais são usadas para representar muitos fenômenos nas ciências naturais e
sociais. A base mais comumente usada é o número e = 2,7182 ..., número irracional chamado
“número de Euler”.
Assim, a função exponencial de base e, f (x) = ex e a função exponencial de base 1/e , f (x) =
(1/e)x = e-x têm os seguintes gráficos:
2.5 Função logarítmica
Dado um número real a, tal que a  1 e a > 0, é dado o nome de função logarítmica de base
a à função f : *   definida por y = logax ou f(x) = logax .
7
Exemplos
a) f ( x )  log 2 x
b) f ( x )  log 1 x
2
c) f ( x )  log e x  ln x
Algumas observações quanto aos logaritmos
 Definição de logaritmo: log a x  y  a y  x , a > 0 e a ≠ 1 (condição de existência).
 Só existe logaritmo de um número positivo, já que a base é positiva (a > 0) e o resultado
de qualquer potência positiva é um número positivo.
 Quando a base não estiver escrita, subentendemos que é a base 10, ou seja,
log10 x  log x .
 Quando a base for o número de Euler, a constante e, chamamos de “logaritmo natural” e
usamos a notação ln, ou seja, log e x  ln x .
Propriedades
8
Gráfico da função logarítmica
O gráfico de uma função logarítmica é uma curva, em que devem ser observadas algumas
particularidades:
 o gráfico nunca corta o eixo das ordenadas (Oy);
 o gráfico corta o eixo das abscissas (Ox) no ponto (1,0), ou seja, 1 é a raiz ou zero da
função;
 os valores de x são sempre positivos.
Seu domínio é o conjunto dos números reais positivos e sua imagem é o conjunto dos
números reais. Ou seja, Dom f =

*

e
Im f =  .
Quanto à base da função, devemos considerar dois casos:
 Base maior que um (a > 1)
f (x) = logax ( a > 1 )
 A função é crescente.
 Dom f =

*

.
 Sua imagem são os reais positivos (Im =  ).
 Para quaisquer x1 e x2 do domínio: x2 > x1  y2 > y1.
 Base entre zero e um (0 < a < 1)
f (x) = logax ( 0 < a < 1 )
 A função é decrescente.
 Dom f =
 * .
 Sua imagem são os reais positivos (Im =  ).
 Para quaisquer x1 e x2 do domínio: x2 > x1  y2 < y1.
9
Da mesma forma que na função exponencial, a base mais comumente usada é o número de
Euler e chamamos este logaritmo de “logaritmo natural”: log e x  ln x .
Exercício: Fazer o esboço do gráfico e determine o domínio e a imagem para cada função abaixo:
1) f(x) = 8x
4) h(x) = ln x
2) g(x) = 8x + 1
5) y  log 1 x
3) y =  1 
 
3
x
2
6) p(x) = 2  ln x
5
10
LISTA COMPLEMENTAR DE EXERCÍCIOS
1)
Dada a função f(x) = 4x – 2, pede-se:
a) o valor de x para o qual se tenha f(x)=0.
b) o valor de x que tem imagem 1.
2)
Sendo f(x+3) = 2x + 4, pede-se:
a) f(0)
b) f(5)
3)
Construa o gráfico das funções abaixo, determinando domínio, imagem, zero da função e sinal
da função.
a) y = x
b) f(x)= 2
c) f(x) =5-3x
d) f(x)=0
4)
Dada a função linear y = ax + b, sabendo-se que f(1) = 6 e f(2) = 11. Encontre a e b.
5)
Encontre a lei da função determinada pelo gráfico abaixo:
6)
Dada a função f, calcule os zeros desta função e represente graficamente, sendo:
a) f ( x )  x 2  7 x  6
b) f ( x )  x 2  2 x  6
c) f ( x )   x 2  2 x  1
d) f ( x )  x 2  3
e) f ( x )   x 2  36
f)
f ( x )  ( x  4)2
g) f ( x )  ( x  9 )2
7) Sendo f ( x )  3 x 2  3 x  3 calcule:
a) f(3)
b)
f (3 )  f ( 3 )
3 3
8) Dadas as funções reais f(x) = x2 – 1 e g(x) = –x2, calcule o valor de f(–1).g(–2).
9) Sendo f(x) = x2 + 2x – 1 e g(x) = x2 , determine os valores de x para os quais f(x) = g(x).
11
10) Determine k, de modo que f(x) = (k – 3)x2 – 4 não possua raízes reais.
11) Dada a função representada pelo gráfico abaixo determine:
a)
b)
c)
d)
e)
Dom f
Im f
os zeros da função;
os intervalos onde a função é crescente e onde é decrescente;
os intervalos onde f é positiva e onde é negativa.
12) A parábola que representa graficamente a função y = –2x2 + bx + c passa pelo ponto (1, 0) e seu
vértice é o ponto de coordenadas (3, k). Determine o valor de k.
13) Escreva a função do 2º grau representada pelo gráfico abaixo.
14) Resolva as equações exponenciais:
15) Determine a solução real da equação:
16) Determinar os valores de x para os quais 2x = 32.
17) Resolver a equação 27x = 243.
12
18) Determinar o valor de x para o qual (1/3)x = 3.
19) Qual é o conjunto solução da equação exponencial 5x+2= 125x?
20) Determinar o conjunto solução do sistema com as duas equações exponenciais: 3x+y = 81 e
3x+y = 1.
21) Resolver a equação exponencial
.
22) Calcule, a partir da definição e de suas respectivas consequências, os seguintes logaritmos:
23) Sabendo que log 2 = a; log 3 = b; log 7 = c, determine:
24) Dado
, calcular A em função de M e N.
25) Seja x um número real positivo. Qual é o valor da base a para que o logaritmo de x na base
a:
26) . Supondo que a, b e c reais positivos, desenvolva, aplicando as propriedades operatórias dos
logaritmos.
27) Calcule a soma S em cada caso:
28) Sabendo que log x + log y = m, determine em função de m:
13
29) Qual o valor de x na equação 10x = 4?
30) Resolva, em ℝ, as seguintes equações:
14