3.2 Cristalografia do Si
3.2 Cristalografia do Si
Do ponto de vista atômico, o silício faz um arranjo atômico onde cada átomo faz 4 ligações.
Num cristal de Si, esses átomos se ligam mantendo as orientações relativas ao longo do
espaço.
Célula
unitária
Constante de rede :
a
Tipo
Diamante
1
Cristalografia : Redes periódicas
3.2 Cristalografia do Si
•  A lâmina de silício constitui um único cristal de Si, onde os átomos se posicionam de
periódica em 3 dimensões.
Célula unitária do Si
( tipo Diamante )
Cristal de Si
(Rede Periódica)
•  Portanto, para entender os detalhes cristalográficos do Si devemos lembrar como são
descritas as redes periódicas de átomos
2
3.2 Cristalografia do Si
Rede periódica Bidimensional
Vetores Unitários
Célula Primitiva
R1 = 5a1 + 3a2
R2 = 2a1 + 4a2
R3 = 4a1 - 1a2
R1 = 2a1 + 3a2
R2 = -2a1 + 4a2
R3 = 4a1 - 1a2
Vetores Unitários
Célula Primitiva
3
3.2 Cristalografia do Si
Rede de Bravais
•  Vemos que a tanto o vetores unitários como as células primitivas não são únicas.
•  Além disso, a célula primitiva não precisa ser construída utilizando os vetores primitivos. Na
verdade, por motivos geométricos, em muitos casos não é conveniente usar os vetores
primitivos :
Rede quadrada
Rede exagonal
R = n 1. a 1 + n 2. a 2
4
Rede de Bravais
3.2 Cristalografia do Si
•  As redes de Bravais são um conceito geométrico e portanto, os pontos da rede não
representam necessariamente átomos.
•  Por exemplo, os pontos podem representar o ponto médio de átomos que vibram ou o
centro de gravidade de moléculas e neste caso não há de fato, átomos nos pontos da
rede.
•  Por outro lado, podemos escolher um dos átomos de um grupo de átomos e este estar
posicionado sobre um dos pontos da rede de Bravais.
5
Redes de Bravais em 2 dimensões
3.2 Cristalografia do Si
Lembrando ...
•  Em 2 dimensões existem 5 redes de Bravais :
6
Redes de Bravais em 3 dimensões
3.2 Cristalografia do Si
•  Em 3 dimensões existem 14 redes de Bravais :
Cúbica
Triclinica
Monoclinica
Exagonal
Rombohédrica
Hortorombica
(trigonal)
Tetragonal
7
Rede de Bravais
3.2 Cristalografia do Si
•  Redes cubicas
8
Exemplos de Redes cúbicas
• Qual é a rede do NaCl
3.2 Cristalografia do Si
Cúbica de face centrada
Qual é a rede ?
•  E a rede do Silício?
Qual é a rede ?
9
Exemplos de Redes cúbicas
3.2 Cristalografia do Si
•  Na família IV da tbela periódica
10
Planos Cristalográficos
3.2 Cristalografia do Si
•  Dada uma rede tridimensional, os átomos definem diversos planos cristalográficos
•  Estes planos podem ser agrupados em famílias, nas quais, todos os planos são
paralelos entre si
•  Note que propriedades como a densidade átomos em cada plano e a distância entre os
planos varia de família para família :
11
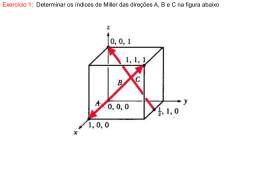
Índices de Miller
•  Considere um plano que cruza os
eixos cartesianos nos pontos : x1,
y1 , z1
3.2 Cristalografia do Si
Exemplo : considere o plano que cruza os eixos
x, e z nos pontos x=2, y=2 e x=3 respctivamente.
Encontre s indices de Miller e desenhe o plano :
z
•  Tome os inversos desses
números :
e multiplique pelo menor número
inteiro que permita eliminar as frações.
y
x
O conjunto dos menores inteiros (h,k,l)
assim obtidos são chamados de
índices de Miller do plano em
questão.
12
Índices de Miller : Exemplos
(1) Dada uma rede cúbica com constante rede “a”,
desenhe e encontre índices de Miller do plano que
cruza os eixos x, y e z nos pontos 1a, ∞ e (1/2)a.
3.2 Cristalografia do Si
(2) Dada uma rede cúbica com constante rede “a”,
desenhe e encontre os índices de Miller do plano
que cruza os eixos x, y e z nos pontos 3a, 1a e 2a.
13
Exercício sobre índices de Miller
3.2 Cristalografia do Si
14
Índices de Miller
3.2 Cristalografia do Si
•  Os Índices de Miller (hkl) de um plano cristalográfico são importantes porque fornecem
diretamente os coeficientes a, b e c da equação geométrica do plano:
ou seja, a=h, b=k e c=l. Mas cuidado, ... isto vale para is índices de Miller mas não para os
pontos onde o plano cruza os eixos !,
•  Lembre que um conjunto incides de Miller (hkl)
representa uma família de planos planos
paralelos, equivalentes e igualmente espaçados
entre si. O que identifica um plano particular é o
coeficiente “d”.
Plano (121)
Plano (121)
•  Por outro lado, como são tomados os menores
inteiros (h,k,l) , os incides de Miller (hkl)
representam o plano mais próximo da origem.
•  Nomenclatura :
  ( h k l ) : Um plano em particular
  { h k l } : Família de planos
  < h k l > : Uma direção em particular
  [ h k l ] : Família de direções
15
Exercício sobre índices de Miller
3.2 Cristalografia do Si
•  Desenhe os planos correspondentes aos índices de Miller indicados :
( 111)
( 110)
(010)
( 001)
( 110)
( 111)
16
Principais planos do Si
(100)
3.2 Cristalografia do Si
(110)
(111)
17
Principais planos do Si
3.2 Cristalografia do Si
18
19
3.2 Cristalografia do Si
Exercício
•  Considere um cristal de Si de 10x10x10 células unitárias. Utilizando as equações dos planos
correspondentes, corte o cristal nas 8 possíveis direções dos planos da família {111} : (1 1 1),
(-1 1 1), (1 -1 1), (-1 -1 1), (1 1 -1), (-1 1 -1), (1 -1 -1), (-1 -1 -1) conforme mostra figura abaixo :
(utilize o programa “simMEMS” )
• 
• 
• 
• 
• 
• 
• 
• 
Plano
a
( 1 1 1) 1
( 1 -1 1 ) 1
( -1 -1 1 ) -1
( -1 1 1 ) -1
( 1 1 -1 ) 1
( 1 -1 -1 ) 1
( -1 -1 -1 ) -1
( -1 1 -1 ) -1
b
1
-1
-1
1
1
-1
-1
1
c
d
1 15 x 5,43
1 -10 x 5,43
1 0
1 -5 x 5,43
-1
-1
-1
-1
20
21