Disciplina : Ciência dos Materiais
LOM 3013 – 2015M1
5 – Pontos, Direções e Planos
Cristalográficos
Prof. Carlos Angelo Nunes
•
Foram estabelecidas convenções para designar as localizações de pontos,
direções e planos no interior de uma célula unitária.
•
A base para determinação dos valores dos índices é a célula unitária com
um sistema de coordenadas, que consiste em três eixos (x,y,z) com origem
em um dos vértices e coincidentes com as arestas da célula unitária.
Coordenadas dos pontos
•
A posição de qualquer ponto localizado no interior de uma célula unitária
pode ser especificada em termos das suas coordenadas na forma de
múltiplos fracionários dos comprimentos das arestas das células unitárias
(isto é, em termos de a, b e c).
• O que significa um ponto de coordenadas ¼ 1 ½ ?
• Especifique as coordenadas dos pontos
para todas as posições atômicas em
uma célula unitária CCC.
Direções Cristalográficas
•
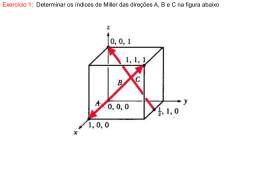
As seguintes etapas são consideradas para determinação dos índices
direcionais:
1- Um vetor com comprimento conveniente é posicionado de maneira tal que ele
passe através da origem do sistema de coordenadas;
2- São determinados os comprimentos das projeções do vetor sobre cada um dos
três eixos; esses são medidos em termos das dimensões a, b e c da célula unitária;
3- Esses três números são multiplicados ou divididos por um fator comum, para
reduzi-los aos menores valores inteiros;
4- Os três índices, sem separação por vírgulas, são colocados entre colchetes:
[uvw].
• Pode haver índices negativos?
•
Para algumas estruturas cristalinas, várias direções não paralelas com
índices diferentes são cristalograficamente equivalentes; isso significa que
o espaçamento entre os átomos ao longo de cada direção é o mesmo.
•
As direções abaixo são cristalograficamente equivalentes no sistema cúbico.



[100][1 00][010][0 1 0][001][00 1]
• As direções [100] e [001] são equivalentes nos cristais com simetria
tetragonal?
Cristais Hexagonais : Utilização de um sistema de coordenadas com quatro eixos,
ou de Miller-Bravais.
Os três eixos a1, a2 e a3 estão contidos em um único plano (chamado plano basal) e
formam ângulos de 120o entre si. O eixo z é perpendicular a esse plano basal.
Conversão do sistema de três índices para o sistema de quatro índices:
[u´v´w´]
[uvwt ]
1
u  (2u´v´)
3
1
v  (2v´u´)
3
t  (u  v)
w  w´
Planos Cristalográficos
Em todos os sistemas cristalinos, à excessão do sistema hexagonal, os planos cristalográficos
são especificados por três índices de Miller na forma (hkl). Quaisquer dois planos paralelos
entre si são equivalentes e possuem índices idênticos.
O procedimento utilizado para determinar os valores dos índices h, k e l é o seguinte:
1- Se o plano passa através da origem que foi selecionada, ou outro plano paralelo deve ser
construído no interior da célula unitária mediante uma translação apropriada, ou uma nova
origem deve ser estabelecida no vértice de outra célula unitária.
2- Desse modo, ou o plano cristalográfico intercepta ou ele é paralelo a um dos três eixos; o
comprimento da interseção planar a cada eixo é determinado em termos dos parâmetros da
rede a, b, c.
3- Os valores inversos desses números são obtidos. Um plano paralelo a um eixo pode ser
considerado como tendo uma interseção no infinito e portanto, um índice igual a zero.
4- Se necessário, esses três números mudados para o conjunto de menores números inteiros
pela multiplicação ou divisão por um fator comum.
5- Finalmente, os índices inteiros, não separados por vírgula, são colocados entre parênteses.
Planos Cristalográficos
Planos Cristalográficos
z
Exemplo:
1.
Interceptos
2.
Reciprocos
3.
Redução
4.
Indices de Miller
Exemplo:
1.
2.
Interceptos
Reciprocos
3.
Redução
4.
Índices de Miller
a
1
1/1
1
1
b
1
1/1
1
1
c

1/
0
0
(110)
a
1/2
1/½
2
2
b

1/
0
0
c
y
b
a
x
z
c

1/
0
0
c
y
a
(100)
x
b
Planos Cristalográficos
z
Exemplo:
1. Interceptos
2. Reciprocos
a
1/2
1/½
2
6
3.
Redução
4.
Indices de Miller
b
1
1/1
1
3
(634)
c
3/4
1/¾
4/3
4
c
a
x



b
y
Planos Cristalográficos
• O arranjo atômico para um plano cristalográfico, que frequentemente é de
interesse, depende da estrutura cristalina
• Uma família de planos contém todos os planos que são cristalograficamente
equivalentes, ou seja, aqueles que tem o mesmo empacotamento atômico.
Quais os planos da família {100} da estrutura cristalina tetragonal?
Densidade Linear (DL)
número..de..átomos..sobre..o..vetor..direção
DL 
comprimento..do..vetor..direção
OBS. Em relação ao número de átomos, é necessário levar em consideração
o compartilhamento dos átomos com as células unitárias adjacentes.
ex: densidade linear do Al na direção [110]
a = 0.405 nm
[110]
# atoms
a
DL 
Comprim.
2
2a
 3.5 nm1
Densidade Planar (DP)
número..de..átomos..no.. plano
DP 
área..do.. plano
Densidade Planar do Fe: Plano (100)
Solução: Para T < 912ºC o ferro tem estrutura CCC.
2D Célula
(100)
a
4 3
R
3
raio do ferro R = 0.1241 nm
átomos
2D célula
Dens. Planar =
área
2D célula
1
a2
=
1
4 3
R
3
2
= 12.1
átomos
átomos
19
= 1.2 x 10
2
nm
m2
Densidade Planar do Fe: Plano (111)
1 átomo no plano / célula
2a
Átomos no plano
Átomos acima do plano
Átomos abaixo do
plano
h
3
a
2
2
átomos
2D célula
 4 3  16 3 2
2
área  2 ah  3 a  3 
R  
R
3
 3

1
átomos =
átomos
0.70 x 1019
= 7.0
2
2
Dens. Planar =
area
2D célula
16 3
3
R
2
nm
m
Estruturas Cristalinas Compactas
•
CFC e HCP : Fator de empacotamento = 0,74.
•
Estas duas estruturas podem ser descritas em termos de empilhamento de
planos compactos. A diferença entre as duas está na sequência desse
empilhamento.
HCP: ABABABAB.....
CFC: ABCABCABC.......
Estruturas Cristalinas Compactas
Estruturas Cristalinas Compactas
z
example
1. Intercepts
2. Reciprocals
3.
Reduction
a1
1
1
1
1
a2

1/
0
0
a3
-1
-1
-1
-1
c
1
1
1
1
a2
a3
4.
Miller-Bravais Indices
(1011)
a1