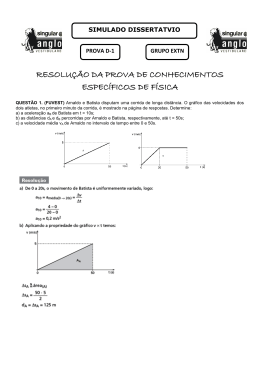
1. (Fuvest 2011) Um automóvel consome, em média, um litro de gasolina para percorrer, em
região urbana, uma distância de 10 km. Esse automóvel é do tipo conhecido como flex, ou
seja, pode utilizar, como combustível, gasolina e/ou álcool, com as propriedades fornecidas na
tabela abaixo. Com base nas informações dadas, determine:
a) Os valores das energias EG e EA liberadas pela combustão de um litro de gasolina e de um
litro de álcool, respectivamente.
b) A distância dA percorrida, em média, pelo automóvel com 1 litro de álcool.
c) O preço máximo Pm de um litro de álcool, acima do qual não seria conveniente, do ponto de
vista financeiro, utilizar esse combustível, caso o litro de gasolina custasse R$ 2,40.
d) O gasto médio G com combustível, por quilômetro rodado pelo automóvel, em região
urbana, usando exclusivamente álcool, se o litro desse combustível custar R$ 1,60.
NOTE E ADOTE
3
poder calorífico (kcal/kg)
densidade (g/cm )
4
gasolina
1,0 x 10
0,7
3
álcool
7,0 x 10
0,8
A distância percorrida pelo automóvel é diretamente proporcional à
energia liberada pelo combustível consumido.
2. (Fuvest 1999) Um músico sopra a extremidade aberta de um tubo de 25cm de comprimento,
fechado na outra extremidade, emitindo um som na frequência f=1.700Hz. A velocidade do som
no ar, nas condições do experimento, é v=340m/s. Dos diagramas a seguir, aquele que melhor
representa a amplitude de deslocamento da onda sonora estacionária, excitada no tubo pelo
sopro do músico é:
3. (Fuvest 1999) Considere três situações em que um raio de luz se desloca no vácuo:
I. nas proximidades de uma esfera carregada eletricamente, representada na figura I.
II. nas proximidades do polo de um imã, representada na figura II.
III. nas proximidades de um fio percorrido por corrente elétrica i, representada na figura III.
Página 1 de 54
Podemos afirmar que o raio de luz
a) não é desviado em qualquer das três situações.
b) é desviado nas três situações.
c) só é desviado nas situações I e II.
d) só é desviado nas situações II e III.
e) só é desviado na situação I.
4. (Fuvest 1998) Uma criança montada em um velocípede se desloca em trajetória retilínea,
com velocidade constante em relação ao chão. A roda dianteira descreve uma volta completa
em um segundo. O raio da roda dianteira vale 24 cm e o das traseiras 16 cm. Podemos afirmar
que as rodas traseiras do velocípede completam uma volta em, aproximadamente;
a) 1/2 s
b) 2/3 s
c) 1 s
d) 3/2 s
e) 2 s
5. (Fuvest 1998) Dois trens A e B fazem manobra em uma estação ferroviária deslocando-se
paralelamente sobre trilhos retilíneos. No instante t = 0 s eles estão lado a lado. O gráfico
representa as velocidades dos dois trens a partir do instante t = 0 s até t = 150 s, quando
termina a manobra. A distância entre os dois trens no final da manobra é:
a) 0 m
b) 50 m
c) 100 m
d) 250 m
e) 500 m
6. (Fuvest 1998) Duas cunhas A e B, de massas MA e MB respectivamente, se deslocam juntas
sobre um plano horizontal sem atrito, com aceleração constante a . sob a ação de uma força
Página 2 de 54
horizontal F aplicada à cunha A, como mostra a figura. A cunha A permanece parada em
relação à cunha B, apesar de não haver atrito entre elas.
a) Determine a intensidade da força F aplicada à cunha A.
b) Determine a intensidade da força vetorial N, que a cunha B aplica à cunha A.
c) Sendo θ o ângulo de inclinação da cunha B, determine a tangente de θ.
7. (Fuvest 1998) Um sistema mecânico é formado por duas polias ideais que suportam três
corpos A, B e C de mesma massa m, suspensos por fios ideais como representado na figura. O
corpo B está suspenso simultaneamente por dois fios, um ligado a A e outro a C.
Podemos afirmar que a aceleração do corpo B será:
a) zero
g
para baixo
3
g
c)
para cima
3
2g
d)
para baixo
3
2g
e)
para cima
3
b)
8. (Fuvest 1998) No anel do Lab. Nac. de Luz Sincrotron em Campinas, SP, representado
8
simplificadamente na figura, elétrons (e) se movem com velocidade u≈c≈3×10 m/s formando
um feixe de pequeno diâmetro, numa órbita circular de raio R = 32m.
Página 3 de 54
O valor da corrente elétrica, devido ao fluxo de elétrons através de uma seção transversal
qualquer do feixe, vale 0,12A.
a) Calcule o número total n de elétrons contidos na órbita.
b) Considere um feixe de pósitrons (p), movendo-se em sentido oposto no mesmo tubo em
órbita a 1cm da dos elétrons, tendo velocidade, raio e corrente iguais as dos elétrons.
Determine o valor aproximado da força de atração F , de origem magnética, entre os dois
feixes, em N.
Dados:
1) Pósitrons são partículas de massa igual à dos elétrons com carga positiva igual em módulo à
dos elétrons.
2) Como R>>d, no cálculo de F , considere que o campo produzido por um feixe pode ser
calculado como o de um fio retilíneo.
-19
3) Carga de 1 elétron q = -1,6×10 coulomb.
4) Módulo do vetor indução magnética B, criando a uma distância r de um fio retilíneo
-7
percorrido por uma corrente i, é: B = 2 × 10 i/r sendo B em tesla (T), i em ampere (A) e r em
metro (m)
9. (Fuvest 1998) Uma esteira rolante transporta 15 caixas de bebida por minuto, de um
°
depósito no sub-solo até o andar térreo. A esteira tem comprimento de 12m, inclinação de 30
com a horizontal e move-se com velocidade constante. As caixas a serem transportadas já são
colocadas com a velocidade da esteira.
Se cada caixa pesa 200N, o motor que aciona esse mecanismo deve fornecer a potência de:
a) 20 W
b) 40 W
c) 300 W
d) 600 W
e) 1800 W
10. (Fuvest 1998) Um brinquedo é constituído por um cano (tubo) em forma de
3
de arco de
4
circunferência, de raio médio R, posicionado num plano vertical, como mostra a figura. O
desafio é fazer com que a bola 1, ao ser abandonada de uma certa altura H acima da
extremidade B, entre pelo cano em A, bata na bola 2 que se encontra parada em B, ficando
nela grudada, e ambas atinjam juntas a extremidade A. As massas das bolas 1 e 2 são M 1 e
M2, respectivamente. Despreze os efeitos do ar e das forças de atrito.
Página 4 de 54
a) Determine a velocidade v com que as duas bolas grudadas devem sair da extremidade B do
tubo para atingir a extremidade A.
b) Determine o valor de H para que o desafio seja vencido.
11. (Fuvest 1998) Um recipiente contém dois líquidos I e II de massas específicas
(densidades) ρ1 e ρ2 respectivamente. Um cilindro maciço de altura h se encontra em equilíbrio
na região da interface entre os líquidos, como mostra a figura. Podemos afirmar que a massa
específica do material do cilindro vale:
(ρ1  2ρ2 )
2
(ρ1  ρ2 )
b)
2
( 2ρ1  2ρ2 )
c)
3
(ρ1  2ρ2 )
d)
3
(ρ  ρ2 )
e) 2 1
3
a)
12. (Fuvest 1998) Considere uma mola ideal de comprimento L0=35cm presa no fundo de uma
piscina vazia (Fig. 1). Prende-se sobre a mola um recipiente cilíndrico de massa m=750g, altura
2
h=12,5cm e secção transversal externa S=300cm , ficando a mola com comprimento L1=20cm
(Fig. 2). Quando, enchendo-se a piscina, o nível da água atinge a altura H, começa a entrar
água no recipiente (Fig. 3).
Página 5 de 54
3
2
Dados: ρ água = 1,0 g/cm ; g = 10 m/s .
a) Qual o valor da tensão T na mola, em N, quando começa a entrar água no recipiente?
b) Qual o valor da altura H, em cm?
13. (Fuvest 1998) Sobre uma mesa horizontal de atrito desprezível, dois blocos A e B de
massas m e 2m, respectivamente, movendo-se ao longo de uma reta, colidem um com o outro.
Após a colisão os blocos se mantém unidos e deslocam-se para a direita com velocidade V ,
como indicado na figura. O ÚNICO esquema que NÃO pode representar os movimentos dos
dois blocos antes da colisão é:
14. (Fuvest 1998) Estamos no ano de 2095 e a "interplanetariamente" famosa FIFA
(Federação Interplanetária de Futebol Amador) está organizando o Campeonato Interplanetário
de Futebol, a se realizar em MARTE no ano 2100. Ficou estabelecido que o comprimento do
campo deve corresponder à distância do chute de máximo alcance conseguido por um bom
jogador. Na TERRA esta distância vale L (T) = 100 m.
Suponha que o jogo seja realizado numa atmosfera semelhante à da TERRA e que, como na
TERRA, possamos desprezar os efeitos do ar, e ainda, que a máxima velocidade que o bom
jogador consegue imprimir à bola seja igual à na TERRA. Suponha que M(M)/M(T) = 0,1 e
R(M)/R(T) = 0,5, onde M(M) e R(M) são a massa e o raio de MARTE e M(T) e R(T) são a
massa e o raio da TERRA.
a) Determine a razão g(M)/g(T) entre os valores da aceleração da gravidade em MARTE e na
TERRA.
b) Determine o valor aproximado L(M), em metros, do comprimento do campo em MARTE.
c) Determine o valor aproximado do tempo t(M), em segundos, gasto pela bola, em um chute
de máximo alcance para atravessar o campo em MARTE.
2
adote g(T) = 10m/s
15. (Fuvest 1998) Considere uma máquina térmica em que n moles de um gás ideal executam
Página 6 de 54
o ciclo indicado no gráfico pressão P versus volume V.
Sendo T a temperatura do gás, considere as relações:
I) Ta = 4Tc e Tb = Td
II) Ta = Tc e Tb = 4Td
Sendo W o trabalho realizado pelo gás no trecho correspondente, considere as relações
III) │ Wab │ = │ Wcd │
IV) │ Wab │ > │ Wcd │
Estão corretas as relações:
a) I e III
b) I e IV
c) II e III
d) II e IV
e) somente III
16. (Fuvest 1998) Deseja-se medir a pressão interna P em um grande tanque de gás. Para
isto, utiliza-se como manômetro um sistema formado por um cilindro e um pistão de área A,
preso a uma mola de constante elástica k. A mola está no seu estado natural (sem tensão)
quando o pistão encosta na base do cilindro, e tem comprimento L 0 (fig1 - registro R fechado).
Abrindo-se o registro R, o gás empurra o pistão, comprimindo a mola, que fica com
comprimento L (fig 2 - registro R aberto).
A pressão ambiente vale P0 e é aplicada no lado externo do pistão. O sistema é mantido à
temperatura ambiente durante todo o processo. O valor da pressão absoluta P no tanque vale:
a) k .
L0  L 
A
+ P0
Página 7 de 54
b) k .
c) k .
L0  L 
A
 L0  L

A
- P0
A.A
d) k . L . A + P0
e) k .
L
- P0
A
17. (Fuvest 1998) Um termōmetro especial, de lķquido dentro de um recipiente de vidro, é constituķdo
de um bulbo de 1cm3 e um tubo com secēćo transversal de 1mm2. Ą temperatura de 20 °C, o lķquido
preenche completamente o bulbo até a base do tubo. Ą temperatura de 50 °C o lķquido preenche o tubo
até uma altura de 12mm. Considere desprezķveis os efeitos da dilataēćo do vidro e da pressćo do gįs
acima da coluna do lķquido. Podemos afirmar que o coeficiente de dilataēćo volumétrica médio do
lķquido vale:
-4 °
-1
a) 3 × 10 C
-4 ° -1
b) 4 × 10 C
-4 ° -1
c) 12 × 10 C
-4 ° -1
d) 20 × 10 C
-4 ° -1
e) 36 × 10 C
18. (Fuvest 1998) As curvas A e B na figura representam a variação de temperatura (T) em
função do tempo (t) de duas substâncias A e B, quando 50g de cada uma é aquecida
°
separadamente, a partir da temperatura inicial de 20 C, na fase sólida, recebendo calor numa
taxa constante de 20cal/s.
Considere agora um experimento em que 50g de cada uma das substâncias são colocadas em
contato térmico num recipiente termicamente isolado, com a substância A na temperatura
°
°
inicial TA=280 C e a substância B na temperatura inicial T B=20 C.
Página 8 de 54
a) Determine o valor do calor latente de fusão LB da substância B.
b) Determine a temperatura de equilíbrio do conjunto no final do experimento.
c) Se a temperatura final corresponder à mudança da fase de uma das substâncias, determine
a quantidade da mesma em cada uma das fases.
19. (Fuvest 1998) Num forno de micro-ondas é colocado um vasilhame contendo 3kg d'água a
°
10 C. Após manter o forno ligado por 14 min, se verifica que a água atinge a temperatura de
°
50 C. O forno é tão desligado e dentro do vasilhame d'água é colocado um corpo de massa 1kg
°
°
e calor específico c=0,2cal/(g C), à temperatura inicial de 0 C. Despreze o calor necessário
para aquecer o vasilhame e considere que a potência fornecida pelo forno é continuamente
absorvida pelos corpos dentro dele. O tempo a mais que será necessário manter o forno ligado,
°
na mesma potência, para que a temperatura de equilíbrio final do conjunto retorne a 50 C é:
a) 56 s
b) 60 s
c) 70 s
d) 280 s
e) 350 s
20. (Fuvest 1998) A curva da figura 1 mostra a dependência do índice de refração n de uma
substância transparente com a frequência f da luz. Três raios de luz 1, 2 e 3, paralelos, incidem
°
segundo um ângulo de 45 sobre a superfície plana de um bloco da substância e são
refratados, conforme indicado na figura 2.
Denominando f1, f2 e f3 as frequências dos raios 1, 2 e 3, respectivamente, se conclui que:
a) f3 < f2 < f1
b) f1 < f2 < f3
c) f2 < f1 < f3
d) f2 < f3 < f1
e) f1 < f3 < f2
21. (Fuvest 1998) Um LASER produz um feixe paralelo de luz, com 4mm de diâmetro.
Utilizando um espelho plano e uma lente delgada convergente, deseja-se converter o feixe
paralelo num feixe divergente propagando-se em sentido oposto. O feixe divergente deve ter
abertura total Φ = 0,4 radiano, passando pelo centro óptico C da lente. A figura a seguir mostra
a configuração do sistema. Como Φ é pequeno, pode-se considerar Φ ≈ senΦ ≈ tgΦ.
Página 9 de 54
Para se obter o efeito desejado, a distância focal f da lente e a distância d da lente ao espelho
deve valer:
a) f = 10 mm; d = 5 mm
b) f = 5 mm; d = 10 mm
c) f = 20 mm; d = 10 mm
d) f = 10 mm; d = 20 mm
e) f = 5 mm; d = 5 mm
22. (Fuvest 1998) Na figura a seguir, em escala, estão representados uma lente L delgada,
DIVERGENTE, com seus focos F, e um espelho plano E, normal ao eixo da lente. Uma fina
haste AB está colocada normal ao eixo da lente. Um observador O, próximo ao eixo e à
esquerda da lente, mas bastante afastado desta, observa duas imagens da haste. A primeira
A1B1, é a imagem direta de AB formada pela lente. A segunda, A2B2, é a imagem, formada pela
lente, do reflexo A'B' da haste AB no espelho E.
a) Construa e identifique as 2 imagens: A1B1 e A2B2
b) Considere agora o raio R, indicado na figura, partindo de A em direção à lente L. Complete a
trajetória deste raio até uma região à esquerda da lente. Diferencie claramente com linha cheia
este raio de outros raios auxiliares.
23. (Fuvest 1998) Quatro pequenas esferas de massa m, estão carregadas com carga de
mesmo valor absoluto q, sendo duas negativas e duas positivas, como mostra a figura. As
esferas estão dispostas formando um quadrado de lado a e giram numa trajetória circular de
centro O, no plano do quadrado, com velocidade de módulo constante v. Suponha que as
ÚNICAS forças atuantes sobre as esferas são devidas à interação eletrostática. A constante de
permissividade elétrica é ε0. Todas as grandezas (dadas e solicitadas) estão em unidades SI.
Página 10 de 54
a) Determine a expressão do módulo da força eletrostática resultante F que atua em cada
esfera e indique sua direção.
b) Determine a expressão do módulo da velocidade tangencial v das esferas.
24. (Fuvest 1998) Três pequenos esferas carregadas com cargas de mesmo módulo, sendo A
positiva e B e C negativas, estão presas nos vértices de um triângulo equilátero. No instante
em que elas são soltas, simultaneamente, a direção e o sentido de suas acelerações serão
melhor representados pelo esquema:
25. (Fuvest 1998) Um capacitor é formado por duas placas paralelas, separadas 10mm entre
sí. Considere as placas do capacitor perpendiculares ao plano do papel. Na figura são
mostradas as intersecções das placas P1 e P2 e de algumas superfícies equipotenciais com o
plano do papel. Ao longo do eixo médio AA', o campo elétrico é uniforme entre as placas e seu
5
valor é E=10 V/m. As superfícies equipotenciais indicadas estão igualmente espaçadas de
-14
1mm ao longo do eixo. Uma carga q=10 C é levada do ponto O ao ponto P, indicados na
figura.
Página 11 de 54
O trabalho realizado é:
a) 0 J
-12
b) 5 × 10 J
-11
c) 1 × 10 J
-12
d) 4 × 10 J
-10
e) 1 × 10 J
26. (Fuvest 1998) Um circuito é formado de duas lâmpadas L1 e L2, uma fonte de 6V e uma
resistência R, conforme desenhado na figura. As lâmpadas estão acesas e funcionando em
seus valores nominais (L1: 0,6W e 3V e L2: 0,3W e 3V).
O valor da resistência R é:
a) 15 Ω
b) 20 Ω
c) 25 Ω
d) 30 Ω
e) 45 Ω
27. (Fuvest 1998) No circuito mostrado na figura a seguir, os três resistores têm valores
R1=2Ω, R2=20Ω e R3=5Ω. A bateria B tem tensão constante de 12V. A corrente i1 é considerada
positiva no sentido indicado. Entre os instantes t=0s e t=100s, o gerador G fornece uma tensão
variável V=0,5t (V em volt e t em segundo).
Página 12 de 54
a) Determine o valor da corrente i1 para t=0s.
b) Determine o instante t0 em que a corrente i1 é nula.
c) Trace a curva que representa a corrente i1 em função do tempo t, no intervalo de 0 a 100s.
Indique claramente a escala da corrente, em ampere (A).
d) Determine o valor da potência P recebida ou fornecida pela bateria B no instante t=90s.
28. (Fuvest 1998) Um fio retilíneo, bastante longo, está no plano de uma espira retangular,
paralelo a um de seus lados, conforme indicado na Figura 1. A corrente I 1 no fio, varia em
função do tempo t conforme indicado na Figura 2. O gráfico que melhor representa a corrente I 2
induzida na espira é:
29. (Fuvest 1998) Considere os dois imãs permanentes mostrados na figura. O externo tem
forma de anel, com quatro polos. O interno, em forma de cruz, pode girar livremente em torno
do eixo O, fixo e coincidente com o eixo do anel. As polaridades N (Norte) e S (Sul) dos polos
(de igual intensidade em módulo) estão representadas na figura. A posição do imã móvel em
relação ao anel é dada pelo ângulo ž. Podemos afirmar que o gráfico que melhor pode
representar o valor do torque (momento de força) total τ, que age sobre o imã móvel, em
função de ž, é:
30. (Fuvest 1998) Uma boia pode se deslocar livremente ao longo de uma haste vertical,
fixada no fundo do mar. Na figura, a curva cheia representa uma onda no instante t = 0s e a
curva tracejada a mesma onda no instante t = 0,2s. Com a passagem dessa onda, a boia
oscila.
Página 13 de 54
Nesta situação, o menor valor possível da velocidade da onda e o correspondente período de
oscilação da boia, valem:
a) 2,5 m/s e 0,2 s
b) 5,0 m/s e 0,4 s
c) 0,5 m/s e 0,2 s
d) 5,0 m/s e 0,8 s
e) 2,5 m/s e 0,8 s
31. (Fuvest 1998) Duas fontes sonoras F1 e F2 estão inicialmente separadas de 2,5m. Dois
observadores A e B estão distantes 10m da fonte F1, sendo que o observador A está no eixo x
e o observador B no eixo y, conforme indica a figura. As duas fontes estão em fase e emitem
som numa frequência fixa f=170Hz.
Num dado instante, a fonte F2 começa a se deslocar lentamente ao longo do eixo x, afastandose da fonte F1. Com este deslocamento, os dois observadores detectam uma variação
periódica na intensidade do som resultante das duas fontes, passando por máximos e mínimos
consecutivos de intensidade. Sabe-se que a velocidade do som é 340m/s nas condições do
experimento.
Levando em conta a posição inicial das fontes, determine:
a) a separação L(a) entre as fontes para a qual o observador A detecta o primeiro mínimo de
intensidade.
b) a separação L(b) entre as fontes para a qual o observador B detecta o primeiro máximo de
intensidade.
32. (Fuvest 1998) Um estudante está prestando vestibular e não se lembra da fórmula correta
que relaciona a velocidade v de propagação do som, com a pressão P e a massa específica ρ
3
a
b
(kg/m ), num gás. No entanto, ele se recorda que a fórmula é do tipo v =C . P /ρ, onde C é uma
constante adimensional. Analisando as dimensões (unidades) das diferentes grandezas físicas,
ele conclui que os valores corretos dos expoente a e b são:
a) a = 1, b = 2
b) a = 1, b = 1
Página 14 de 54
c) a = 2, b = 1
d) a = 2, b = 2
e) a = 3, b = 2
33. (Fuvest 1997) Dois satélites artificiais A e B descrevem órbitas circulares no plano
equatorial da Terra. O satélite A está a uma distância RA do centro da Terra e estacionário com
relação a um observador fixo em um ponto do equador da Terra.
a) Esse mesmo observador vê o satélite B passar por uma mesma posição, numa vertical
sobre ele, a cada dois dias, sempre à mesma hora. Quais os dois possíveis valores da
velocidade angular de B, no referencial inercial em relação ao qual a Terra gira em torno de
seu eixo com um período de 24 h? Expresse o resultado em rd/h.
b) Calcule, em função de RA, os valores dos raios das órbitas correspondentes às velocidades
angulares encontradas no item anterior.
34. (Fuvest 1997) Um carro se desloca numa trajetória retilínea e sua velocidade em função do
tempo, a partir do instante t = 10 s, está representada no gráfico a seguir. Se o carro partiu do
repouso e manteve uma aceleração constante até t =15 s, a distância percorrida, desde sua
partida até atingir a velocidade de 6 m/s, vale:
a) 12,5 m
b) 18,0 m
c) 24,5 m
d) 38,0 m
e) 84,5 m
35. (Fuvest 1997) Os corpos A, B e C têm massas iguais. Um fio inextensível e de massa
desprezível une o corpo C ao B, passando por uma roldana de massa desprezível. O corpo A
está apoiado sobre o B. Despreze qualquer efeito das forças de atrito. O fio f mantém o sistema
em repouso. Logo que o fio f é cortado, as acelerações aA, aB e aC dos corpos A, B e C serão,
Página 15 de 54
g
g
; aC = ;
2
2
g
g
g
b) aA =
; aB =
; aC =
;
3
3
3
g
g
c) aA = 0 ; aB =
; aC =
3
3
a) aA = 0 ; aB =
d) aA = 0 ; aB = g ; aC = g
e) aA =
g
g
g
; aB =
; aC =
2
2
2
36. (Fuvest 1997) Uma bolinha pendurada na extremidade de uma mola vertical executa um
movimento oscilatório. Na situação da figura, a mola encontra-se comprimida e a bolinha está
subindo com velocidade V . Indicando por V a força da mola e por P(vetorial) a força peso
aplicadas na bolinha, o único esquema que pode representar tais forças na situação descrita
anteriormente é
37. (Fuvest 1997) Um automóvel com massa de 1000 kg percorre, com velocidade constante v
= 20 m/s
(ou 72 km/h), uma estrada (ver figura) com dois trechos horizontais (1 e 3), um em subida (2) e
um em descida (4). Nos trechos horizontais o motor do automóvel desenvolve uma potência de
30k W para vencer a resistência do ar, que pode ser considerada constante ao longo de todo o
2
trajeto percorrido. Suponha que não há outras perdas por atrito. Use g = 10 m/s .
São dados: sen α = 0,10 e sen β = 0,15.
Determine:
a) o valor, em newtons, da componente paralela a cada trecho da estrada das forças F 1, F2, e
F4, aplicadas pela estrada ao automóvel nos trechos 1, 2 e 4, respectivamente.
b) o valor, em kW, da potência P2 que o motor desenvolve no trecho 2.
Página 16 de 54
38. (Fuvest 1997) Um atleta está dentro de um elevador que se move para cima com
velocidade constante V. Ele começa a levantar uma massa de 100 kg, inicialmente apoiada no
piso do elevador, quando este passa pela altura z = 0,0 m, e termina quando o piso do elevador
passa por z = 27,0 m. A massa é levantada pelo atleta até uma altura de 2,0 m acima do piso
do elevador. O trabalho realizado pelo atleta sobre a massa é W. A variação da energia
potencial da massa durante o levantamento, em relação ao referencial da Terra, é ∆U.
2
Podemos afirmar, usando g = 10 m/s , que
a) W = 2.000 J e ∆U = 2.000 J
b) W = 2.000 J e ∆U = 29.000 J
c) W = 27.000 J e ∆U = 27.000 J
d) W = 2.000 J e ∆U = 27.000 J
e) W = 29.000 J e ∆U = 29.000 J
39. (Fuvest 1997) Um cilindro maciço, de massa m = 45 kg, altura H = 0,30 m e base de área
2
S = 0,050 m está imerso em água, como mostra a figura I, sendo mantido em equilíbrio
2
estático por um fio fino ao qual se aplica uma tensão T 0. Use g = 10 m/s e considere a massa
3
específica da água ρm = 1000 kg/m .
Começa-se então a puxar o cilindro na direção y, para cima, com velocidade constante e muito
pequena.
a) Trace no papel de gráfico a seguir o valor, em newtons, da tensão T no fio em função da
posição y da base inferior do cilindro, desde y = - 0,70 m até y = + 0,50 m. Marque os valores
da escala utilizada no eixo da tensão T.
b) Determine o trabalho total W, em joules, realizado pela tensão T, para o deslocamento
descrito no item a.
40. (Fuvest 1997) Um avião que voa a grande altura é pressurizado para conforto dos
passageiros. Para evitar sua explosão é estabelecido o limite máximo de 0,5 atmosfera para a
diferença entre a pressão interna no avião e a externa. O gráfico representa a pressão
atmosférica P em função da altura H acima do nível mar. Se o avião voa a uma altura de 7.000
Página 17 de 54
metros e é pressurizado até o limite, os passageiros ficam sujeitos a uma pressão igual à que
reina na atmosfera a uma altura de aproximadamente
a) 0 m
b) 1.000 m
c) 2.000 m
d) 5.500 m
e) 7.000 m
41. (Fuvest 1997) Duas esferas de aço, ocas e rígidas com 1 kg de massa e 3 litros de volume
estão cheias de ar e são mantidas submersas e em equilíbrio, muito próximas à superfície de
um lago, por forças de valor F dirigidas para baixo, como mostra a figura. A esfera A é
totalmente fechada e a esfera B tem um pequeno furo em sua parte inferior o qual permite a
entrada da água. Puxa-se as duas esferas até uma profundidade de 10 metros a seguir da
superfície do lago. Para mantê-las em equilíbrio nesta profundidade, os novos valores das
forças FA e FB, aplicadas respectivamente nas esferas A e B, são tais que
a) FA > F
b) FA = F
c) FA > F
d) FA > F
e) FA = F
e FB < F
e FB = F
e FB > F
e FB = F
e FB < F
42. (Fuvest 1997) Um conjunto de dois carrinhos com um rapaz sentado no carrinho dianteiro,
e nele preso pelo cinto de segurança, encontra-se inicialmente na altura h (posição A da figura)
de uma montanha russa. A massa m do rapaz é igual à massa de cada um dos carrinhos. O
conjunto começa a descida com velocidade inicial nula. Ao chegar ao ponto B da parte plana
da trajetória, o rapaz solta o carrinho traseiro e o empurra para trás com impulso suficiente para
fazê-lo retornar ao ponto A de partida, onde o carrinho chega com velocidade nula. Despreze
os atritos.
Página 18 de 54
a) Determine a altura máxima H a que chega o carrinho dianteiro.
b) Houve variação de energia mecânica do conjunto quando o rapaz empurrou o carrinho
traseiro? Se houve, calcule essa variação. Se não houve, escreva "a energia mecânica se
conservou".
43. (Fuvest 1997) Uma pequena esfera de massa de modelar está presa na extremidade de
um fio formando um pêndulo de comprimento L. A esfera é abandonada na posição I e, ao
atingir o ponto inferior II de sua trajetória, se choca com outra esfera igual ficando grudadas
uma na outra e depois prosseguindo juntas até atingirem uma altura máxima h =
L
. Considere
4
a hipótese de que as três grandezas físicas dadas a seguir se conservam. Com relação a essa
hipótese, a única alternativa de acordo com o que aconteceu durante a colisão é
a) Energia cinética - FALSA / Quantidade de movimento - VERDADEIRA / Energia mecânica
total - VERDADEIRA
b) Energia cinética - VERDADEIRA / Quantidade de movimento - FALSA / Energia mecânica
total - VERDADEIRA
c) Energia cinética - VERDADEIRA / Quantidade de movimento - VERDADEIRA / Energia
mecânica total - VERDADEIRA
d) Energia cinética - FALSA / Quantidade de movimento - FALSA / Energia mecânica total FALSA
e) Energia cinética - FALSA / Quantidade de movimento - VERDADEIRA / Energia mecânica
total - FALSA
44. (Fuvest 1997) Uma pirâmide reta, de altura H e base quadrada de lado L, com massa m
uniformemente distribuída, está apoiada sobre um plano horizontal. Uma força F com direção
paralela ao lado AB é aplicada no vértice V. Dois pequenos obstáculos O, fixos no plano,
impedem que a pirâmide se desloque horizontalmente. A força F capaz de fazer tombar a
pirâmide deve ser tal que
Página 19 de 54
mgH
a) │ F │ >
2
L
2
2 H
 
b) │ F │> mg
c) │ F │>
mgH
L
2
mg
d) │ F │>
L
2
H
mg
e) │ F │>
L
2
2
L
2
2 H
 
45. (Fuvest 1997) Uma certa massa de gás ideal sofre uma compressão isotérmica muito lenta
passando de um estado A para um estado B. As figuras representam diagramas TP e TV,
sendo T a temperatura absoluta, V o volume e P a pressão do gás. Nesses diagramas, a
transformação descrita anteriormente só pode corresponder às curvas
Página 20 de 54
a) I e IV
b) II e V
c) III e IV
d) I e VI
e) III e VI
46. (Fuvest 1997) Um mol de gás ideal é levado lentamente do estado inicial A ao estado final
C, passando pelo estado intermediário B. A Figura l representa a variação do volume, V do
gás, em litros (ℓ), em função da temperatura absoluta T, para a transformação em questão.
A constante universal dos gases vale R = 0,082 atm.ℓ/(mol . K).
a) Dentre as grandezas pressão, volume e temperatura, quais permanecem constantes no
trecho AB? E no trecho BC?
b) Construa na Figura 2 o gráfico da pressão P em função da temperatura absoluta T. Indique
claramente os pontos correspondentes aos estados A, B e C. Marque os valores da escala
utilizada no eixo da pressão P.
c) Escreva a função P (T) que representa a pressão P do gás em função da temperatura
absoluta T, no intervalo de 300 K a 600 K, com seus coeficientes dados numericamente.
47. (Fuvest 1997) Dois termômetros de vidro idênticos, um contendo mercúrio (M) e outro água
°
°
(A), foram calibrados em 0 C e 37 C, obtendo-se as curvas M e A, da altura da coluna do
líquido em função da temperatura. A dilatação do vidro pode ser desprezada. Considere as
seguintes afirmações:
°
°
I - O coeficiente de dilatação do mercúrio é aproximadamente constante entre 0 C e 37 C.
II - Se as alturas das duas colunas forem iguais a 10 mm, o valor da temperatura indicada pelo
termômetro de água vale o dobro da indicada pelo de mercúrio.
°
III - No entorno de 18 C o coeficiente de dilatação do mercúrio e o da água são praticamente
iguais.
Página 21 de 54
Podemos afirmar que só são corretas as afirmações
a) I, II e III
b) I e II
c) I e III
d) II e III
e) I
48. (Fuvest 1997) Dois recipientes de material termicamente isolante contêm cada um 10 g de
°
água a 0 C. Deseja-se aquecer até uma mesma temperatura os conteúdos dos dois
recipientes, mas sem misturá-los. Para isso é usado um bloco de 100 g de uma liga metálica
°
inicialmente à temperatura de 90 C. O bloco é imerso durante um certo tempo num dos
recipientes e depois transferido para o outro, nele permanecendo até ser atingido o equilíbrio
térmico. O calor específico da água é dez vezes maior que o da liga. A temperatura do bloco,
por ocasião da transferência, deve então ser igual a
°
a) 10 C
°
b) 20 C
°
c) 40 C
°
d) 60 C
°
e) 80 C
49. (Fuvest 1997) Um pesquisador estuda a troca de calor entre um bloco de ferro e certa
quantidade de uma substância desconhecida, dentro de um calorímetro de capacidade térmica
desprezível (ver Figura 1). Em sucessivas experiências, ele coloca no calorímetro a substância
°
desconhecida, sempre no estado sólido à temperatura T 0 = 20 C, e o bloco de ferro, a várias
temperaturas iniciais T, medindo em cada caso a temperatura final de equilíbrio térmico Te. O
gráfico da Figura 2 representa o resultado das experiências. A razão das massas do bloco de
ferro e da substância desconhecida é mf/ms = 0,8. Considere o valor do calor específico do
°
ferro igual a 0,1 cal/(g C). A partir destas informações, determine para a substância
desconhecida:
a) a temperatura de fusão, Tfusão.
b) o calor específico, cs, na fase sólida.
c) o calor latente de fusão L.
50. (Fuvest 1997) Um holofote é constituído por dois espelhos esféricos côncavos E1 e E2, de
modo que a quase totalidade da luz proveniente da lâmpada L seja projetada pelo espelho
maior E1, formando um feixe de raios quase paralelos. Neste arranjo, os espelhos devem ser
posicionados de forma que a lâmpada esteja aproximadamente
Página 22 de 54
a) nos focos dos espelhos E1 e E2.
b) no centro de curvatura de E2 e no vértice de E1.
c) no foco de E2 e no centro de curvatura de E1.
d) nos centros de curvatura de E1 e E2.
e) no foco de E1 e no centro de curvatura de E2.
51. (Fuvest 1997) Um raio de luz I, no plano da folha, incide no ponto C do eixo de um
°
semicilindro de plástico transparente, segundo um ângulo de 45 com a normal OC à face
°
plana. O raio emerge pela superfície cilíndrica segundo um ângulo de 30 com a direção de OC.
Um raio II incide perpendicularmente à superfície cilíndrica formando um ângulo θ com a
direção OC e emerge com direção praticamente paralela à face plana. Podemos concluir que
°
a) θ = 0
°
b) θ = 30
°
c) θ = 45
°
d) θ = 60
e) a situação proposta no enunciado não pode ocorrer
52. (Fuvest 1997) A figura representa uma lente convergente L, com focos F e F', e um
quadrado ABCD, situado num plano que contém o eixo da lente. Construa, na própria figura, a
imagem A'B'C'D' do quadrado, formada pela lente. Use linhas tracejadas para indicar todas as
linhas auxiliares utilizadas para construir as imagens. Represente com traços contínuos
somente as imagens dos lados do quadrado, no que couber na folha. Identifique claramente as
imagens A', B', C', e D' dos vértices.
Página 23 de 54
53. (Fuvest 1997) Quando se aproxima um bastão B, eletrizado positivamente, de uma esfera
metálica, isolada e inicialmente descarregada, observa-se a distribuição de cargas
representada na Figura 1.
Mantendo o bastão na mesma posição, a esfera é conectada à terra por um fio condutor que
pode ser ligado a um dos pontos P, R ou S da superfície da esfera. Indicando por (  ) o
sentido do fluxo transitório (∅) de elétrons (se houver) e por (+), (-) ou (0) o sinal da carga final
(Q) da esfera, o esquema que representa ∅ e Q é
54. (Fuvest 1997) Duas cargas pontuais positivas, q1 e q2 = 4q1, são fixadas a uma distância d
uma da outra. Uma terceira carga negativa q3 é colocada no ponto P entre q1 e q2, a uma
distância X da carga q1, conforme mostra a figura.
a) Calcule o valor de X para que a força sobre a carga q3 seja nula.
b) Verifique se existe um valor de q3 para o qual tanto a carga q1 como a q2 permanecem em
equilíbrio, nas posições do item a), sem necessidade de nenhuma outra força além das
eletrostáticas entre as cargas. Caso exista, calcule este valor de q 3; caso não exista, escreva
"não existe" e justifique.
Página 24 de 54
55. (Fuvest 1997) Quatro cargas pontuais estão colocadas nos vértices de um quadrado. As
duas cargas +Q e -Q têm mesmo valor absoluto e as outras duas, q1 e q2, são desconhecidas.
Afim de determinar a natureza destas cargas, coloca-se uma carga de prova positiva no centro
do quadrado e verifica-se que a força sobre ela é F , mostrada na figura a seguir. Podemos
afirmar que
a) q1 > q2 > 0
b) q2 > q1 > 0
c) q1 + q2 > 0
d) q1 + q2 < 0
e) q1 = q2 > 0
56. (Fuvest 1997) O circuito da figura é formado por 4 pilhas ideais de tensão V e dois
resistores idênticos de resistência R. Podemos afirmar que as correntes i1 e i2, indicadas na
figura, valem
a) i1 = 2
V
R
b) i1 = zero
c) i1 = 2
V
R
d) i1 = zero
e) i1 = 2
V
R
V
e i2 = 2
R
V
e i2 = 2
R
V
e i2 = 4
R
e i2 = 4
V
e i2 = zero
R
Página 25 de 54
57. (Fuvest 1997) Na figura é esquematizada uma máquina de solda elétrica. São feitas medidas
da voltagem V em função, da corrente I que circula através do arco, obtendo-se a curva
mostrada na figura.
Nos gráficos I e II, as curvas que qualitativamente melhor representam a potência dissipada P
e a resistência R(R = V/I) do arco, em função da corrente I são, respectivamente
a) A e Z
b) C e Z
c) B e Y
d) A e X
e) B e X
58. (Fuvest 1997) O circuito a seguir é formado por quatro resistores e um gerador ideal que
fornece uma tensão V = 10 volts. O valor da resistência do resistor R é desconhecida. Na figura
estão indicados os valores das resistências dos outros resistores.
a) Determine o valor, em ohms, da resistência R para que as potências dissipadas em R 1, e R2
sejam iguais.
b) Determine o valor, em watts, da potência P dissipada no resistor R1, nas condições do item
anterior.
59. (Fuvest 1997) Três imãs iguais em forma de barra, de pequena espessura, estão sobre um
plano. Três pequenas agulhas magnéticas podem girar nesse plano e seus eixos de rotação
estão localizados nos pontos A, B e C. Despreze o campo magnético da Terra. A direção
assumida pelas agulhas, representadas pela figura I, é melhor descrita pelo esquema:
Página 26 de 54
60. (Fuvest 1997) Uma jovem, repousando à margem de um canal, observa uma garrafa
levada pela correnteza com velocidade VA e um barquinho B preso às margens por fios fixados
nos pontos M e N. no canal se propaga uma onda com velocidade V0 > VA no MESMO
SENTIDO que a correnteza. Todas as velocidades são medidas em relação à jovem. A
distância entre cristas sucessivas da onda, representadas no desenho por C1, C2 e C3, é λ. A
jovem vê então a garrafa e o barquinho oscilando para cima e para baixo com frequências f A e
fB que valem
V
VA
e fB = 0


V
V
b) fA = V0 - A e fB = V0 + A


V
V
c) fA = 0 e fB = V0 - A


V
V
d) fA = V0 - A e fB = 0


V
V
e) fA = 0 e fB = 0


a) fA = V0 +
61. (Fuvest 1997) O som de frequência mais baixa, dita fundamental, emitido por um tubo
sonoro fechado numa extremidade, corresponde a um comprimento de onda igual a quatro
vezes o comprimento L do tubo. Sabe-se que o valor v da velocidade do som no ar pode ser
obtido pela expressão v = 20 T , onde v é em m/s e T é a temperatura absoluta do ar em
kelvin (K). Quando o tubo contém ar e estando ambos a 300 K (temperatura ambiente), a
frequência fundamental emitida é f0 = 500 hertz.
Página 27 de 54
a) Determine o comprimento L do tubo.
b) Desprezando a dilatação do tubo, determine a temperatura T, comum ao tubo e ao ar nele
contido, na qual a frequência fundamental emitida é 2 f 0.
c) Considerando agora a dilatação do tubo, o valor da frequência fundamental emitida à
temperatura T, calculada no item anterior, será maior, igual ou menor do que 2 f 0? Justifique.
62. (Fuvest 1997) No Sistema Internacional de Unidades (SI), as sete unidades de base são o
metro (m), o quilograma (kg), o segundo (s), o kelvin (K), o ampere (A), a candela (cd) e o mol
(mol). A lei de Coulomb da eletrostática pode ser representada pela expressão F = (1/4πε0)(Q1
2
Q2/r ).
onde ε0 é uma constante fundamental da física e sua unidade, em função das unidades de
base do SI, é
-2 2 2
a) m s A
-3
-1 2
b) m kg A
-3
-1 4 2
c) m kg s A
d) m kg s-2
e) adimensional
63. (Fuvest 1996) Dois veículos A e B deslocam-se em trajetórias retilíneas e paralelas uma à
outra. No instante t = 0 s eles se encontram lado a lado. O gráfico adiante representa as
velocidades dos dois veículos, em função do tempo, a partir desse instante e durante os 1200 s
seguintes. Os dois veículos estarão novamente lado a lado, pela primeira vez, no instante
a) 400 s.
b) 500 s.
c) 600 s.
d) 800 s.
e) 1200 s.
64. (Fuvest 1996) Um carro viaja com velocidade de 90 km/h (ou seja, 25 m/s) num trecho
retilíneo de uma rodovia quando, subitamente, o motorista vê um animal parado na sua pista.
Entre o instante em que o motorista avista o animal e aquele em que começa a frear, o carro
2
percorre 15 m. Se o motorista frear o carro à taxa constante de 5,0 m/s , mantendo-o em sua
trajetória retilínea, ele só evitará atingir o animal, que permanece imóvel durante todo o tempo,
se o tiver percebido a uma distância de, no mínimo,
a) 15 m.
b) 31,25 m.
c) 52,5 m.
d) 77,5 m.
e) 125 m.
65. (Fuvest 1996) Num toca fitas, a fita F do cassete passa em frente da cabeça de leitura C
com uma velocidade constante v = 4,80 cm/s. O diâmetro do núcleo dos carretéis vale 2,0 cm.
Com a fita completamente enrolada num dos carretéis, o diâmetro externo do rolo de fita vale
5,0 cm. A figura adiante representa a situação em que a fita começa a se desenrolar do carretel
Página 28 de 54
A e a se enrolar no núcleo do carretel B.
Enquanto a fita é totalmente transferida de A para B, o número de rotações completas por
segundos (rps) do carretel A
a) varia de 0,32 a 0,80 rps.
b) varia de 0,96 a 2,40 rps.
c) varia de 1,92 a 4,80 rps.
d) permanece igual a 1,92 rps.
e) varia de 11,5 a 28,8 rps.
66. (Fuvest 1996) Dois vagões de massa M1 e M2 estão interligados por uma mola de massa
desprezível e o conjunto é puxado ao longo de trilhos retilíneos e horizontais por uma força que
tem a direção dos trilhos. Tanto o módulo da força quanto o comprimento da mola podem variar
com o tempo. Num determinado instante os módulos da força e da aceleração do vagão de
massa M1 valem, respectivamente F e a1, tendo ambas o mesmo sentido. O módulo da
aceleração do vagão de massa M2 nesse mesmo instante, vale
a)
F
 M1a1 
M2
b)
F
.
M1  M2 
c)
F
.
M2
.
 F 
 - a1.
 M2 
d) 
 F 
 + a1.
 M2 
e) 
67. (Fuvest 1996) Tenta-se, sem sucesso, deslocar uma caixa de peso P = 50 N, em repouso
Página 29 de 54
sobre um plano horizontal com atrito, aplicando-lhe uma força F = 200 N, na direção da haste.
Despreze a massa da haste.
a) Faça um esquema de todas as forças que agem sobre a caixa e identifique claramente a
origem de cada uma delas. Escreva o valor, em N, da resultante dessas forças (FR).
b) Qual o valor da força de atrito entre a caixa e o plano (em N)?
c) Qual o valor mínimo do coeficiente de atrito?
68. (Fuvest 1996) Um corpo C de massa igual a 3 kg está em equilíbrio estático sobre um
plano inclinado, suspenso por um fio de massa desprezível preso a uma mola fixa ao solo,
como mostra a figura a seguir. O comprimento natural da mola (sem carga) é L0 = 1,2 m e ao
sustentar estaticamente o corpo ela se distende, atingindo o comprimento L = 1,5 m. Os
possíveis atritos podem ser desprezados. A constante elástica da mola, em N/m, vale então
a)
b)
c)
d)
e)
10.
30.
50.
90.
100.
69. (Fuvest 1996) Um jogador de basquete arremessa uma bola B em direção à cesta. A figura
1, a seguir, representa a trajetória da bola e sua velocidade v num certo instante.
Desprezando os efeitos do ar, as forças que agem sobre a bola, nesse instante, podem ser
representadas por:
Página 30 de 54
70. (Fuvest 1996) Um pequeno corpo de massa m é abandonado em A com velocidade nula e
escorrega ao longo do plano inclinado, percorrendo a distância d = AB . Ao chegar a B,
verifica-se que sua velocidade é igual a
gh . Pode-se então deduzir que o valor da força de
atrito que agiu sobre o corpo, supondo-a constante, é
a) zero.
b) mgh.
c) mgh/2.
d) mgh/2d.
e) mgh/4d.
71. (Fuvest 1996) Um carro de corrida, com massa total m = 800 kg, parte do repouso e, com
aceleração constante, atinge, após 15 segundos, a velocidade de 270 km/h (ou seja 75 m/s). A
figura representa o velocímetro, que indica a velocidade instantânea do carro. Despreze as
perdas por atrito e as energias cinéticas de rotação (como a das rodas do carro). Suponha que
o movimento ocorre numa trajetória retilínea e horizontal.
a) Qual a velocidade angular ω do ponteiro do velocímetro durante a aceleração do carro?
Indique a unidade usada.
b) Qual o valor do módulo da aceleração do carro nesses 15 segundos?
c) Qual o valor da componente horizontal da força que a pista aplica ao carro durante sua
aceleração?
d) Qual a potência fornecida pelo motor quando o carro está a 180 km/h?
Página 31 de 54
72. (Fuvest 1996) Um carro alegórico do bloco carnavalesco "Os Filhos do Nicolau" possui um
plano inclinado e se move com velocidade horizontal U constante em relação à pista. Albert, o
filho mais moço, escorrega desde o alto da rampa sem atrito. É observado por Galileu, o mais
velho, sentado no carro, e por Isaac, parado na pista. Quando Albert chega ao fim da rampa,
Isaac observa que a componente horizontal da velocidade de Albert é nula. Suponha que o
movimento de Albert não altera a velocidade do carro, muito mais pesado do que ele.
°
2
São dados: H = 5,0 m, θ = 30 . Adote g = 10 m/s
a) Quais os valores das componentes horizontal Vh e vertical Vv da velocidade de Albert no fim
da rampa, observados por Galileu?
b) Quanto vale U?
c) Qual o valor da componente vertical Vv da velocidade de Albert no fim da rampa, observado
por Isaac?
73. (Fuvest 1996) Uma pequena bolha de ar, partindo da profundidade de 2,0 m abaixo da
superfície de um lago, tem seu volume aumentado em 40% ao chegar à superfície. Suponha
que a temperatura do lago seja constante e uniforme e que o valor da massa específica da
3
3
2
água do lago seja ρ = 1,0 × 10 kg/m . Adote g = 10 m/s e despreze os efeitos de tensão
superficial.
a) Qual a variação do valor da pressão do ar dentro da bolha, em N/m nessa subida?
2
b) Qual o valor da pressão atmosférica, em N/m , na superfície do lago?
74. (Fuvest 1996) Icebergs são blocos de gelo flutuantes que se desprendem das geleiras
polares. Se apenas 10% do volume de um iceberg fica acima da superfície do mar e se a
3
massa específica da água do mar vale 1,03 g/cm , podemos afirmar que a massa específica do
3
gelo do iceberg, em g/cm , vale, aproximadamente:
a) 0,10.
b) 0,90.
c) 0,93.
d) 0,97.
Página 32 de 54
e) 1,00.
75. (Fuvest 1996) Num jogo de vôlei, o jogador que está junto à rede salta e "corta" uma bola
(de massa m = 0,30 kg) levantada na direção vertical, no instante em que ela atinge sua altura
máxima, h = 3,2 m. Nessa "cortada" a bola adquire uma velocidade de módulo V, na direção
paralela ao solo e perpendicular à rede, e cai exatamente na linha de fundo da quadra. A
distância entre a linha de meio da quadra (projeção da rede) e a linha de fundo é d = 9,0 m.
2
Adote g = 10 m/s .
Calcule:
a) o tempo decorrido entre a cortada e a queda da bola na linha de fundo.
b) a velocidade V que o jogador transmitiu à bola.
c) o valor do módulo da variação da quantidade de movimento, ∆Q, do centro de massa do
jogador, devida à cortada.
d) a intensidade média da força, F, que o jogador aplicou à bola, supondo que o tempo de
-2
contato entre a sua mão e a bola foi de 3,0 × 10 s.
76. (Fuvest 1996) Uma quantidade de barro de massa 2,0 kg é atirada de uma altura h = 0,45 m, com
uma velocidade horizontal v = 4 m/s, em direção a um carrinho parado, de massa igual a 6,0 kg, como
mostra a figura adiante. Se todo o barro ficar grudado no carrinho no instante em que o atingir, o carrinho
iniciará um movimento com velocidade, em m/s, igual a
a)
3
.
4
b) 1.
c)
5
.
4
d) 2.
e) 3.
77. (Fuvest 1996) Um congelador doméstico ("freezer") está regulado para manter a
°
°
temperatura de seu interior a - 18 C. Sendo a temperatura ambiente igual a 27 C (ou seja, 300
K), o congelador é aberto e, pouco depois, fechado novamente. Suponha que o "freezer" tenha
boa vedação e que tenha ficado aberto o tempo necessário para o ar em seu interior ser
°
trocado por ar ambiente. Quando a temperatura do ar no "freezer" voltar a atingir - 18 C, a
pressão em seu interior será:
a) cerca de 150% da pressão atmosférica.
b) cerca de 118% da pressão atmosférica.
c) igual à pressão atmosférica.
d) cerca de 85% da pressão atmosférica.
e) cerca de 67% da pressão atmosférica.
78. (Fuvest 1996) Um ser humano adulto e saudável consome, em média, uma potência de
3
120 J/s. Uma "caloria alimentar" (1 kcal) corresponde, aproximadamente, a 4 × 10 J. Para nos
Página 33 de 54
mantermos saudáveis, quantas "calorias alimentares" devemos utilizar, por dia, a partir dos
alimentos que ingerimos?
a) 33
b) 120
3
c) 2,6 × 10
3
d) 4,0 × 10
5
e) 4,8 × 10
°
79. (Fuvest 1996) A energia necessária para fundir um grama de gelo a 0 C é oitenta vezes
°
maior que a energia necessária para elevar de 1 C a temperatura de um grama de água.
°
Coloca-se um bloco de gelo a 0 C dentro de um recipiente termicamente isolante fornecendose, a seguir, calor a uma taxa constante. Transcorrido um certo intervalo de tempo observa-se
o término da fusão completa do bloco de gelo. Após um novo intervalo de tempo, igual à
°
METADE do anterior, a temperatura da água, em C, será:
a) 20.
b) 40.
c) 50.
d) 80.
e) 100.
80. (Fuvest 1996) Um recipiente de paredes finas contém 100 g de uma liga metálica. O
gráfico representa a temperatura T da liga em função do tempo t.
Até o instante t = 50 s, a liga recebe de um aquecedor a potência P0 = 30 W e, a partir desse
°
instante, passa a receber a potência P1 = 43 W. A temperatura de fusão da liga é 327 C e a de
°
ebulição é superior a 1500 C. Na situação considerada a liga perde calor para o ambiente a
uma taxa constante. Avalie:
a) a quantidade de calor perdida pela liga, a cada segundo, em J.
b) a energia (em J) necessária para fundir 1 g da liga.
°
c) a energia (em J) necessária para elevar, de 1 C, a temperatura de 1 g da liga no estado
líquido.
°
d) a energia (em J) necessária para elevar, de 1 C, a temperatura de 1 g da liga no estado
sólido.
81. (Fuvest 1996) Numa folha de papel num plano horizontal, está desenhado um círculo de
centro C. Sobre a folha é colocada uma placa grossa de vidro, cobrindo metade do círculo. A
figura 1, a seguir mostra uma pessoa olhando para o círculo, com seu olho no eixo vertical OC.
A alternativa que melhor representa o que a pessoa enxerga é:
Página 34 de 54
82. (Fuvest 1996) Um indivíduo idoso perdeu a acomodação para enxergar de perto,
permanecendo sua visão acomodada para uma distância infinita. Assim, só consegue ver
nitidamente um objeto pontual quando os raios de luz, que nele se originam, atingem seu olho
(O) formando um feixe paralelo. Para ver de perto, ele usa óculos com lentes convergentes L,
de distância focal f. Ele procura ver uma pequena esfera P, colocada a uma distância
constante, d = 0,4f, de um espelho E. A esfera é pintada de preto na parte voltada para a lente
e de branco na parte voltada para o espelho.
A figura I refere-se aos itens a) e b) e representa o observador enxergando nitidamente a parte
preta da esfera.
a) Na figura dada, trace, com clareza, três raios de luz que se originam na esfera e atravessam
a lente passando pelo seu centro C e pelos pontos A e B.
b) Determine o valor da distância Xp, em função de f.
A figura II refere-se aos itens c) e d) e representa o observador enxergando nitidamente a parte
branca da esfera.
c) Na figura a seguir, trace, com clareza, três raios de luz que se originam na esfera, se
refletem no espelho, e atravessam a lente passando pelo seu centro C e pelos pontos A e B.
d) Determine o valor da distância Xb, em função de f.
As figuras a seguir não estão em escala.
83. (Fuvest 1996) Aproximando-se uma barra eletrizada de duas esferas condutoras,
inicialmente descarregadas e encostadas uma na outra, observa-se a distribuição de cargas
esquematizada na figura 1, a seguir.
Em seguida, sem tirar do lugar a barra eletrizada, afasta-se um pouco uma esfera da outra.
Finalmente, sem mexer mais nas esferas, move-se a barra, levando-a para muito longe das
esferas. Nessa situação final, a alternativa que melhor representa a distribuição de cargas nas
duas esferas é:
Página 35 de 54
84. (Fuvest 1996) O módulo F da força eletrostática entre duas cargas elétricas pontuais q 1 e
q2, separadas por uma distância d, é F =
kq1q2
d2
onde k é uma constante. Considere as três
cargas pontuais representadas na figura adiante por + Q, - Q e q. O módulo da força
eletrostática total que age sobre a carga q será
a)
b)
c)
d)
e)
2kQq
.
R2
3kQq
.
R2
kQ2 q
.
R2
 3 

 KQq .
 2  R2


 3 
2

 KQ q .
 2  R2


 
 
85. (Fuvest 1996) Considere um circuito formado por 4 resistores iguais, interligados por fios
perfeitamente condutores. Cada resistor tem resistência R e ocupa uma das arestas de um
cubo, como mostra a figura a seguir. Aplicando entre os pontos A e B uma diferença de
potencial V, a corrente que circulará entre A e B valerá:
Página 36 de 54
a)
b)
c)
d)
e)
4V
.
R
2V
.
R
V
.
R
V
.
2R
V
.
4R
86. (Fuvest 1996) Você dispõe dos elementos: uma bateria para automóvel B e inúmeras
lâmpadas incandescentes dos tipos L1 e L2 caracterizadas na figura a seguir. Em suas
respostas use apenas esses elementos e represente com linhas contínuas os fios de ligação.
Identifique claramente os elementos utilizados.
a) Esquematize uma montagem utilizando 6 lâmpadas, sendo pelo menos uma de cada tipo,
que fiquem acesas em suas condições nominais (indicadas na figura) e determine a corrente
fornecida pela bateria.
b) Esquematize, se possível, uma montagem utilizando apenas 3 lâmpadas que fiquem acesas
em suas condições nominais e determine a corrente fornecida pela bateria. Caso seja
impossível, escreva "impossível" e justifique.
87. (Fuvest 1996) No circuito elétrico residencial a seguir esquematizado, estão indicadas, em
watts, as potências dissipadas pelos seus diversos equipamentos. O circuito está protegido por
um fusível, F, que funde quando a corrente ultrapassa 30 A, interrompendo o circuito. Que
outros aparelhos podem estar ligados ao mesmo tempo que o chuveiro elétrico sem "queimar"
o fusível?
Página 37 de 54
a) Geladeira, lâmpada e TV.
b) Geladeira e TV.
c) Geladeira e lâmpada.
d) Geladeira.
e) Lâmpada e TV.
88. (Fuvest 1996) A figura esquematiza um ímã permanente, em forma de cruz de pequena
espessura, e oito pequenas bússolas, colocadas sobre uma mesa. As letras N e S
representam, respectivamente, polos norte e sul do ímã e os círculos representam as bússolas
nas quais você irá representar as agulhas magnéticas. O ímã é simétrico em relação às retas
NN e SS. Despreze os efeitos do campo magnético terrestre.
a) Desenhe na própria figura algumas linhas de força que permitam caracterizar a forma do
campo magnético criado pelo ímã, no plano da figura.
b) Desenhe nos oito círculos da figura a orientação da agulha da bússola em sua posição de
equilíbrio. A agulha deve ser representada por uma flecha (  ) cuja ponta indica o seu polo
norte.
89. (Fuvest 1996) A figura I adiante representa um imã permanente em forma de barra, onde N
e S indicam, respectivamente, polos norte e sul. Suponha que a barra seja dividida em três
pedaços, como mostra a figura II.
Colocando lado a lado os dois pedaços extremos, como indicado na figura III, é correto afirmar
que eles
Página 38 de 54
a) se atrairão, pois A é polo norte e B é polo sul.
b) se atrairão, pois A é polo sul e B é polo norte.
c) não serão atraídos nem repelidos.
d) se repelirão, pois A é polo norte e B é polo sul.
e) se repelirão, pois A é polo sul e B é polo norte.
90. (Fuvest 1996) Um rádio receptor opera em duas modalidades: uma, AM, cobre o intervalo
de 550 a 1550 khz e outra, FM, de 88 a 108 MHz. A velocidade das ondas eletromagnéticas
8
vale 3 x 10 m/s. Quais, aproximadamente, o menor e o maior comprimentos de ondas que
podem ser captados por esse rádio?
a) 0,0018 m e 0,36 m.
b) 0,55 m e 108 m.
c) 2,8 m e 545 m.
3
6
d) 550 x10 e 108 x 10 m.
14
16
e) 1,6 x 10 m e 3,2 x 10 m.
91. (Fuvest 1996) A figura representa, no instante t = 0 s, a forma de uma corda esticada e
presa entre duas paredes fixas, na qual dois pulsos (I e II) se propagam, sem mudar de forma,
com velocidade de módulo v = 4 m/s nos sentidos indicados. Não há dissipação de energia na
corda.
a) Indique na figura a seguir, por meio de setas (para cima ou para baixo), os sentidos das
velocidades na direção do eixo y, dos pontos A e B, no instante t = 0 s. Se alguma dessas
velocidades for nula, escreva "nula" e a identifique.
b) Determine o valor do módulo da velocidade na direção do eixo y, do ponto A, no instante t =
0 s.
c) Desenhe a forma da corda no instante t = 1 s. Indique por meio de setas os sentidos das
velocidades na direção do eixo y, dos pontos C e D. Se alguma dessas velocidades for nula,
escreva "nula", identificando-a.
Página 39 de 54
92. (Fuvest 1996) Numa aula prática de Física, três estudantes realizam medidas de pressão.
Ao invés de expressar seus resultados em pascal, a unidade de pressão no Sistema
Internacional (SI), eles apresentam seus resultados nas seguintes unidades do SI.
-2
I) Nm
-3
II) Jm
-3
III) Wsm
Podem ser considerados corretos, de ponto de vista dimensional, os seguintes resultados:
a) Nenhum.
b) Somente I.
c) Somente I e II.
d) Somente I e III.
e) Todos.
93. (Fuvest 1995) Uma torneira mal fechada pinga a intervalos de tempo iguais. A figura a
seguir mostra a situação no instante em que uma das gotas está se soltando. Supondo que
cada pingo abandone a torneira com velocidade nula e desprezando a resistência do ar, podese afirmar que a razão
a)
b)
c)
d)
e)
A
entre a distância A e B mostrada na figura (fora de escala) vale:
B
2.
3.
4.
5.
6.
94. (Fuvest 1995) Dois carros percorrem uma pista circular, de raio R, no mesmo sentido, com
velocidades de módulos constantes e iguais a v e 3v. O tempo decorrido entre dois encontros
sucessivos vale:
a) π R/3v.
b) 2π R/3v.
c) π R/v.
d) 2π R/v.
e) 3π R/v.
95. (Fuvest 1995) O motor de um foguete de massa m é acionado em um instante em que ele
se encontra em repouso sob a ação da gravidade ( g constante). O motor exerce uma força
constante perpendicular à força exercida pela gravidade. Desprezando-se a resistência do ar e
a variação da massa do foguete, podemos afirmar que, no movimento subsequente, a
velocidade do foguete mantém:
a) módulo nulo.
b) módulo constante e direção constante.
Página 40 de 54
c) módulo constante e direção variável.
d) módulo variável e direção constante.
e) módulo variável e direção variável.
96. (Fuvest 1995) Uma locomotiva de massa M está ligada a um vagão de massa 2M/3,
ambos sobre trilhos horizontais e retilíneos. O coeficiente de atrito estático entre as rodas da
locomotiva e os trilhos é μ, e todas as demais fontes de atritos podem ser desprezadas. Ao se
por a locomotiva em movimento, sem que suas rodas patinem sobre os trilhos, a máxima
aceleração que ela pode imprimir ao sistema formado por ela e pelo vagão vale:
a) 3μg/5
b) 2μg/3
c) μg
d) 3μg/2
e) 5μg/3
97. (Fuvest 1995) A figura a seguir mostra, num plano vertical, parte dos trilhos do percurso
circular de uma "montanha russa" de um parque de diversões. A velocidade mínima que o
carrinho deve ter, ao passar pelo ponto mais alto da trajetória, para não desgrudar dos trilhos
vale, em metros por segundos:
a)
20 .
b)
40 .
c)
80 .
d)
160 .
e)
320 .
98. (Fuvest 1995) A melhor explicação para o fato de a Lua não cair sobre a Terra é que:
a) a gravidade terrestre não chega até a Lua.
b) a Lua gira em torno da Terra.
c) a Terra gira em torno do seu eixo.
d) a Lua também é atraída pelo Sol.
e) a gravidade da Lua é menor que a da Terra.
99. (Fuvest 1995) Dois pequenos corpos A e B de massas iguais a M, estão presos às
extremidades de uma barra rígida, de massa desprezível e de comprimento L. O sistema gira
livremente sobre um plano horizontal em torno de um pino P fixo no plano, como mostra a
figura adiante. Despreze qualquer o atrito. O sistema é posto em rotação, sendo V A o módulo
constante da velocidade do corpo A.
Página 41 de 54
a) Qual o módulo VB da velocidade do corpo B?
b) Qual o valor da razão entre os módulos das forças resultantes que agem nos corpos A e B,
respectivamente?
c) Determine, em função dos dados do problema, o valor do módulo Fy da força que o pino P
exerce sobre a barra.
100. (Fuvest 1995) Um corpo de massa m está em movimento circular sobre um plano
horizontal, preso por uma haste rígida de massa desprezível e comprimento R. A outra
extremidade da haste está presa a um ponto fixo P, como mostra a figura a seguir (em
perspectiva). O coeficiente de atrito entre o corpo e o plano é μ, constante. Num dado instante,
o corpo tem velocidade de módulo V e direção paralela ao plano e perpendicular à haste.
a) Qual deve ser o valor de V para que o corpo pare após 2 (duas) voltas completas?
b) Qual o tempo gasto pelo corpo para percorrer a última volta antes de parar?
c) Qual o trabalho realizado pela força de atrito durante a última volta?
Página 42 de 54
Gabarito:
Resposta da questão 1:
4
3
3
a) Dados: pG = 1,0  10 kcal/kg; pA = 7,0  10 kcal/kg; dG = 0,7 g/cm = 0,7 kg/L; dA = 0,8
3
g/cm = 0,8 kg/L.
Calculando a massa correspondeste ao volume de 1 litro, para os dois combustíveis:
mG = dG V = 0,7 (1)  mG = 0,7 kg;
mA = dA V = 0,8 (1)  mA = 0,8 kg.
Calculando a energia liberada por litro, para os dois combustíveis:
4
3
EG = mG pG = 0,7 (1,0  10 )  EG = 7,0  10 kcal.
3
3
EA = mA pA = 0,8 (7,0  10 )  EA = 5,6  10 kcal.
b) O enunciado afirma (na tabela) que a distância percorrida (D) é diretamente proporcional à
energia liberada pelo combustível consumido. Então:
DA DG
DA
10



 DA  8 km.
3
EA EG
5,6  10
7  103
c) Dado: PG = R$ 2,40.
O preço máximo do álcool (Pm) acima do qual não seria mais conveniente usar álcool é
aquele que proporciona a mesma razão entre o preço e a distância percorrida relativamente
a gasolina.
Assim:
Pm PG
Pm 2,40



 Pm  R$ 1,92.
DA DG
8
10
d) Dado: PA = R$ 1,60.
P
1,60
G= A 
DA
8

G = R$ 0,20.
Resposta da questão 2:
[E]
Resposta da questão 3:
[A]
Resposta da questão 4:
[B]
Resposta da questão 5:
[D]
Resposta da questão 6:
a) (MA + MB) a
b)
[(MB a )2 + (MA g )2]
c) MB a / MA g
Resposta da questão 7:
[C]
Página 43 de 54
Resposta da questão 8:
11
a) n ≈ 5,02 x 10 elétrons
5
b) F ≈ 5,78 x 10 N
Resposta da questão 9:
[C]
Resposta da questão 10:
a) v =
Rg / 2
2
b) H = [(M1 + M2)/M1] .
R
4
Resposta da questão 11:
[D]
Resposta da questão 12:
a) T = 30 N
b) H = 107,5 cm
Resposta da questão 13:
[D]
Resposta da questão 14:
a) 0,4
b) 250 m
c) 11 s
Resposta da questão 15:
[D]
Resposta da questão 16:
[A]
Resposta da questão 17:
[B]
Resposta da questão 18:
a) O calor latente de fusão de B = 1200 cal. O calor específico latente de fusão de B = 24
cal/g.
°
b) 80 C
c) Fase sólida: 100/3 g
d) Fase líquida: 50/3 g
Resposta da questão 19:
[C]
Resposta da questão 20:
[E]
Resposta da questão 21:
[A]
Resposta da questão 22:
Página 44 de 54
a) Podemos dividir as construções das imagens A 1B1 e A2B2 em dois esquemas mostrados
nas figuras adiante.
A figura I mostra a imagem A1B1 e a figura II mostra a imagem A2B2, do objeto A'B' - reflexo da
haste AB no espelho E.
b) Para lentes que obedecem às condições de Gauss, todos os raios de luz provenientes do
ponto objeto (A) darão origem a um único ponto imagem (A1).
Resposta da questão 23:
a) A resultante das forças indicadas tem direção da diagonal, sentido apontado para o centro e
intensidade:
2
2
R = 1/(4πε0) . q /a . ( 2 -
b) v =


q


1
)
2

2 

) 
1/ (4πε0 ) . 1/ a.m . (1 
4  


Resposta da questão 24:
[B]
Resposta da questão 25:
[D]
Resposta da questão 26:
[D]
Resposta da questão 27:
a) i1 = 2A
Página 45 de 54
b) t = 30 s
c) Marcando os pontos de (a) e (b) no gráfico, temos:
d) P = 48 W
Resposta da questão 28:
[E]
Resposta da questão 29:
[E]
Resposta da questão 30:
[E]
Resposta da questão 31:
a) La = 3 m
b) Lb ≈ 6,63 m
Resposta da questão 32:
[C]
Resposta da questão 33:
a) ω =
π
π
rd/h ou ω =
rd/h
24
8
b) No primeiro caso (órbita externa ao estacionário): R B = RA 3 4 .
4
.
9
No segundo caso (primeira órbita interna ao estacionário): RB = RA 3 
Página 46 de 54
Resposta da questão 34:
[B]
Resposta da questão 35:
[A]
Resposta da questão 36:
[A]
Resposta da questão 37:
a) F1 = 1500 N, F2 = 2500 N, F4 = 0
b) P2 = 50 kW
Resposta da questão 38:
[B]
Resposta da questão 39:
a) Observe o gráfico a seguir:
b) W = 457,5 joules.
Resposta da questão 40:
[B]
Resposta da questão 41:
[E]
Resposta da questão 42:
a) H = 4h
b) ∆ Energia mecânica = 6 mgh
Página 47 de 54
Resposta da questão 43:
[E]
Resposta da questão 44:
[D]
Resposta da questão 45:
[C]
Resposta da questão 46:
a) No trecho AB a pressão é constante. No trecho BC o volume permanece constante.
b) Observe o gráfico a seguir:
c) p = 1/300T
Resposta da questão 47:
[C]
Resposta da questão 48:
[D]
Resposta da questão 49:
°
a) 60 C.
°
b) 0,28 cal/ C
c) 20 cal/g
Resposta da questão 50:
[E]
Resposta da questão 51:
[C]
Página 48 de 54
Resposta da questão 52:
Observe a construção a seguir:
Resposta da questão 53:
[E]
Resposta da questão 54:
d
.
3
4
b) q3 = - q1
9
a) x =
Resposta da questão 55:
[D]
Resposta da questão 56:
[B]
Resposta da questão 57:
[A]
Resposta da questão 58:
a) R = 6 Ω
b) P = 1,28 W
Resposta da questão 59:
[A]
Resposta da questão 60:
[D]
Resposta da questão 61:
a) L =
3
metros.
10
b) T = 1200 K
c) Se λ = 4 . L, a dilatação do tubo vai corresponder a um aumento de λ. como a velocidade da
onda é constante e f = v/λ, concluí-se que a frequência se reduz.
Resposta da questão 62:
[C]
Resposta da questão 63:
[D]
Resposta da questão 64:
[D]
Resposta da questão 65:
[A]
Resposta da questão 66:
[A]
Página 49 de 54
Resposta da questão 67:
a) Observe a figura a seguir:
b) 100 N.
c) 0,45.
Resposta da questão 68:
[C]
Resposta da questão 69:
[E]
Resposta da questão 70:
[D]
Resposta da questão 71:
 π 
 rad/s.
 20 
a) 
2
b) 5,0 m/s .
c) 4000 N.
5
d) 2,0.10 W.
Resposta da questão 72:
a) Vh = 5,0 3 m/s, Vv = 5 m/s .
b) U = 5,0 3 m/s.
c) 5 m/s.
Resposta da questão 73:
4
2
a) - 2,0.10 N/m .
Página 50 de 54
4
2
b) 5,0.10 N/m .
Resposta da questão 74:
[C]
Resposta da questão 75:
1
a) 8,0.10 s.
b) 11,25 m/s.
c) 3,375 kg m/s.
d) 112,5 N.
Resposta da questão 76:
[B]
Resposta da questão 77:
[D]
Resposta da questão 78:
[C]
Resposta da questão 79:
[B]
Resposta da questão 80:
a) 30 J.
b) 26 J.
2
c) 6,5.10 J.
1
d) 1,3.10 J.
Resposta da questão 81:
[B]
Resposta da questão 82:
A figura a seguir faz referência aos itens a e c.
Página 51 de 54
b) 1,4 f.
d) 0,6 f.
Resposta da questão 83:
[A]
Resposta da questão 84:
[B]
Resposta da questão 85:
[A]
Resposta da questão 86:
Observe a figura a seguir:
Resposta da questão 87:
[E]
Resposta da questão 88:
Observe as figuras a seguir.
Página 52 de 54
Resposta da questão 89:
[E]
Resposta da questão 90:
[C]
Resposta da questão 91:
Observe as figuras a seguir:
Resposta da questão 92:
[E]
Resposta da questão 93:
[C]
Resposta da questão 94:
[C]
Resposta da questão 95:
[D]
Resposta da questão 96:
[A]
Resposta da questão 97:
[C]
Resposta da questão 98:
[B]
Página 53 de 54
Resposta da questão 99:
a) VA/2
b) 2
2
c) 3M VA /4L
Resposta da questão 100:
a) 2 (2.π.μ.g.R) .
b)
2 ( π.R)
.
μ.g
c) - μ.m.g.2.π.R.
Página 54 de 54