MATEMÁTICA
Professores Arthur, Denilton, Elizeu e Rodrigo
LISTA DE EXERCÍCIOS 05
01. (UEFS-BA) Seis cubos iguais são colocados empilhados,
um sobre o outro, formando um paralelepípedo retângulo
de volume igual a 4.374 m3.
O perímetro, em metros, de uma das faces do cubo, é
igual a:
a) 18
b) 36
c) 48
d) 72
e) 81
02. (Fac. Ruy Barbosa-BA)
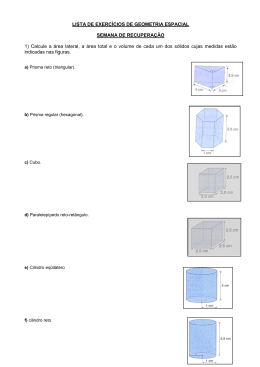
04. Qual a área lateral de um prisma reto de 10 cm de altura,
cuja base é um hexágono regular de apótema 3 3 cm?
a) 320 cm2
b) 340 cm2
c) 360 cm2
d) 380 cm2
05. Dá-se um prisma quadrangular regular cuja área total mede
3
110 m2, sendo a área de uma face lateral os
da área da
5
base. Determine o volume do sólido.
a) 65 m3
b) 75 m3
c) 85 m3
d) 95 m3
e) 105 m3
06. (Cesgranrio-RJ) Se a diagonal de uma face de um cubo
mede 5 2 , então o volume desse cubo é:
a) 600 3
b) 625
d) 125
c) 225
e) 100 3
Um bloco usado em construção tem a forma de um
paralelepípedo reto de dimensões 10 3 cm, 10 3 cm e
15 cm, sendo transpassado por 6 furos, também na forma
de paralelepípedos retos de base quadrada de lado x.
Nessas condições, o volume do material usado para
fabricar o bloco é dado pela expressão:
a)
b)
c)
d)
e)
V = 15(30 – 6x2)
V = 30(15 – x2)
V = 50(90 – 6x2)
V = 45(10 – 6x2)
V = 90(50 – x2)
07. (Unifor-CE) A soma dos comprimentos de todas as
arestas de um cubo é igual a 60 metros. A diagonal, em
metros, mede:
a)
3
b) 3 3
c) 5 3
d) 7 3
08. (PUC-SP) Um cubo tem área total igual a 72 m2. Sua
diagonal vale:
a) 2 6 m
b) 6 m
03. (UCSal-BA) No prisma reto de base triangular, da figura,
todas as arestas medem 2 m.
c)
6m
d)
12 m
e) 2 24 m
09. (FGV-SP) Um cubo tem 96 m2 de área total. De quanto
deve ser aumentada a sua aresta para que seu volume se
torne igual a 216 m3?
O volume desse prisma, em metros cúbicos, é:
a) 2 2
b) 2 3
d) 4 2
c) 4
e) 4 3
a)
b)
c)
d)
e)
1m
0,5 m
9m
2m
3m
2
10. (PUC-MG) A medida do co-seno do ângulo formado por
uma diagonal de um cubo e por cada uma das arestas
concorrentes em um mesmo vértice é igual a:
a)
b)
c)
1
16. (Mackenzie-SP) Dispondo-se de uma folha de
cartolina, medindo 50 cm de comprimento por 30 cm de
largura, pode-se construir uma caixa aberta, cortando-se
um quadrado de 8 cm de lado em cada canto da folha.
O volume dessa caixa, em cm3, será:
2
1
3
2
3
a) 1.244
3
d)
2
b) 1.828
c) 2.324
3
e)
d) 3.808
2
e) 12.000
11. (Unicamp-SP) Procura-se construir um cubo grande,
empilhando cubos pequenos e todos iguais. Quando se
colocar um certo número de cubos pequenos em cada
aresta, sobram cinco. Se tentasse acrescentar um cubo
a mais em cada aresta, ficariam faltando trinta e dois.
Quantos são os cubos pequenos?
17. (UFC-CE) As dimensões da base de um paralelepípedo
retângulo P são 3 m e 5 m, respectivamente, e o seu
volume é 60 m3. O comprimento, em metros, do maior
segmento de reta que une dois pontos de P é igual a:
a) 2 5
12. (UFES) Uma formiga move-se na superfície de um cubo
de aresta a. O menor caminho que ela deve seguir para ir
de um vértice ao vértice oposto tem comprimento:
a) a 2
(
b) 3 5
c) 4 5
d) 5 2
)
b) a 3
d) 1 + 2 a
c) 3 a
e) a 5
e) 6 2
13. (Uneb-BA) O espaço interno de uma caixa d'água tem
forma de um cubo com 1 metro de aresta.
18. (UFC-CE) Os cinco cubos idênticos e justapostos
formam uma cruz cuja área é 198 cm2. Então, o volume,
em cm3, de cada cubo é igual a:
Estando a caixa completamente cheia e retirando-se dela
10 litros, o nível de água diminui, em metros:
a) 2 2
a) 10–5
b) 10–4
c) 10–3
b) 3 3
–2
d) 10
e) 10–1
c) 8
d) 27
14. (UEL-PR) Afigura abaixo representa um hexaedro
regular. A área da secção (ABCD) é
do sólido, em m3, é:
e) 64
2
6 m . O volume
a) 3 3
b) 24 3
c) 33 9
d) 4 27
e) 3
15. (UFBA) Considere um paralelepípedo retângulo, de
dimensões x, y, z. A soma dessas dimensões é 8; o dobro
de x adicionado à soma de y com z é 9; z adicionado ao
triplo da soma de x com y é 16. Sendo d a medida da
diagonal desse paralelepípedo, determine d2.
19. (UFBA) A altura de um copo de forma cilíndrica circular
13
é igual a
de raio de sua base; a metade da sorna da
10
altura do copo com o diâmetro da base mede 16,5 m.
Determine o número que exprime a medida da altura de
outro copo em forma de cone que tem o mesmo diâmetro
e a mesma área lateral de um copo cilíndrico.
20. (Uneb-BA) Num cubo, de volume igual a 64 cm3; está
inscrito um cilindro reto de volume yp cm3. O valor de y é:
a) 8
b) 16
c) 24
d) 48
e) 64
21. (UFBA-BA) A aresta de um cubo e o raio da base de
um cilindro circular reto são iguais a 2 m; a área total da
superfície do cubo é igual á área lateral do cilindro.
x
Sabendo-se que a altura do cilindro é m, determine x.
p
3
22. (UCSal-BA) Um recipiente tem a forma de um cilindro
reto cujo raio da base mede 20 cm.
Se, ao colocar-se uma pedra nesse tanque, o nível da
água subir 0,8 mm, o volume dessa pedra será de,
aproximadamente:
a)
b)
c)
d)
e)
3
101,5 cm
100,5 cm3
97,5 cm3
95,8 cm3
94,6 cm3
23. (UFBA) Considerando-se um prisma triangular regular
de altura 1,8 m e lado da base 1,2 m, pode-se afirmar que:
(01) a área da base do prisma é 1,44 m2.
(02) o volume do prisma é 648 3 dm3.
(04) a área lateral do prisma é 648 dm2.
(08) o raio do círculo circunscrito à base é 0,4 3 m.
(16) o volume do prisma é o triplo do volume da
pirâmide, que tem base e altura iguais às do prisma.
3
(32) a razão entre o lado da base e seu apótema é
.
2
(64) o lado do quadrado de área igual à da base do
prisma é 0,6 m.
24. (UFBA) Considere um plano passando pelo centro de
um prisma hexagonal regular e perpendicular a uma
aresta da base que corta o prisma segundo um quadrado
de diagonal
6 m.
28. (Mackenzie-SP) A altura de um cilindro é 20.
Aumentando-se o raio desse cilindro de 5, a área lateral
do novo cilindro fica igual à área total do primeiro. O raio
do primeiro cilindro é igual a:
a) 10
b) 8
c) 12
29. Para encher um reservatório de água que tem a forma de
um cilindro circular reto, são necessárias 5 horas. Se o
raio da base é 3m e a altura 10 m, o reservatório recebe
água à razão de:
a) 18 p m3 por hora;
b) 30 p m3 por hora;
c) 6 p m3 por hora;
25. (Uneb-BA) A razão entre o volume de um cilindro de
raio r e altura 2r e o volume de um cubo de aresta igual a
altura do cilindro é:
a) 4 p
a) 2(L + 1)
2(L + 2)
b)
L
L+2
c)
2
b) 2 p
4p
c)
3
26. (UFG-GO) Um pedaço de cano, de 30 cm de
comprimento e 10 cm de diâmetro interno, encontra-se na
posição vertical e possui a parte inferior vedada.
Colocando-se dois litros de água em seu interior, a água:
a)
b)
c)
d)
e)
ultrapassa o meio do cano;
transborda;
não chega ao meio do cano;
enche o cano até a borda;
atinge exatamente o meio do cano.
27. (PUC-RS) Dois cilindros, um de altura 4 p e outro de
altura 6 p, têm para perímetro de suas bases 6 e 4,
respectivamente. Se V1 é o volume do primeiro e V2 o
volume do segundo, então:
a) V1 = V2
b) V1 = 2V2
c) V1 = 3V2
d) 2V1 = 3V2
e) 2V1 = V2
d)
L
2
e) 4
31. (UFMG) As áreas das superfícies laterais de dois
cilindros retos V1 e V2, de bases circulares, são iguais.
Se as alturas e os raios das bases dos dois cilindros são,
respectivamente, H1, R1, H2, R2, pode-se afirmar que a
razão entre os volumes de V1 e V2, nessa ordem, é:
a)
H1
H2
b)
R1
R2
c)
p
d)
4
p
e)
12
d) 20 p m3 por hora;
e) 10 p m3 por hora.
30. (UFBA) L + 2 é o volume de um cilindro cuja área
lateral é L. O raio do cilindro é igual a:
3
Sendo x m o volume do prisma, determine 10x.
d) 5
e) 6
H12
H2
32. (Fuvest-SP) A uma caixa d'água de forma cúbica com 1
metro de lado está acoplado um cano cilíndrico com 4 cm
de diâmetro e 50 m de comprimento. Num certo instante,
a caixa está cheia de água e o cano vazio. Solta-se a água
pelo cano até que fique cheio. Qual o valor aproximado
da altura da água na caixa no instante em que o cano
ficou cheio?
a)
b)
c)
d)
e)
90 cm
92 cm
94 cm
96 cm
98 cm
33. (Cesgranrio-RJ) Um tonel cilíndrico, sem tampa e cheio
de água, tem 10 dm de altura e 5 dm de raio da base.
Inclinando-se o tonel de 45°, o volume da água
derramada é, aproximadamente:
a)
b)
c)
d)
e)
145 dm3
155 dm3
263 dm3
353 dm3
392 dm3
4
34. (FCMSC-SP) Um cilindro com eixo horizontal de 15 m
de comprimento e diâmetro interno de 8 m contém
álcool. A superfície livre do álcool determina um
retângulo de área 90 m2. Qual o desnível entre essa
superfície e a geratriz de apoio do cilindro?
a) 6 m
b)
c)
d)
e)
7m
(4 - 7 ) m
(4 + 7 )m
(4 - 7 ) m ou (4 + 7 )m
35. (Consultec-BA) Se a sequência (4x, 2x + 1, x – 1) é um
PG, então, o valor de x é:
1
8
b) – 8
a) -
c) – 1
d) 8
1
e)
8
36. (UFSM-RS) Os termos x, x + 9 e x + 45 estão em PG
nesta ordem.
A razão desta progressão é:
a)
b)
c)
d)
45
9
4
3
4
e)
3
40. (Consultec-BA) A soma de três números em PG
crescente é 26 e o termo do meio é 6. O maior desses
números é dado por:
a)
b)
c)
d)
e)
36
18
24
12
16
41. (UFAL) O produto dos três primeiros termos de uma
PG é 216. Se a razão dessa progressão é – 3, o quinto
termo é:
a)
b)
c)
d)
e)
162
54
18
– 54
– 162
42. (Mackenzie-SP) Numa PG de quatro termos, a soma
dos termos de ordem ímpar é cinco e a soma dos termos
de ordem par é dez.
O quarto termo dessa progressão é igual a:
a)
b)
c)
d)
e)
5
6
7
8
9
43. (UEL-PR) Os divisores positivos do número 310 são
30, 31, 32, 33 etc. A soma de todos esses divisores é:
(3
)
(
)
(
)
-1
2
310 - 1
2
39 - 1
2
310
310 – 1
11
37. (Mackenzie-SP) Se o oitavo termo de uma progressão
1
1
geométrica é e a razão também é , o primeiro termo
2
2
dessa progressão é:
a)
b)
c)
d)
2–1
2
26
28
e)
8
1
2
38. (UGF-RJ) Em uma PG, o primeiro termo é 4 e o quinto
termo é 324. A razão dessa PG é:
a)
b)
c)
d)
3
4
5
2
1
e)
2
39. (Fuvest-SP) O quinto e o sétimo termos de uma PG de
razão positiva valem, respectivamente, 10 e 16. O sexto
termo dessa PG é:
a) 13
b) 10 6
c) 4
d) 4 10
e) 10
a)
b)
c)
d)
e)
44. (Vunesp) No dia 1o de dezembro, uma pessoa enviou pela
Internet uma mensagem para x pessoas. No dia 2, cada
uma dessas pessoas que recebeu a mensagem no dia 1o
enviou a mesma para outras duas novas pessoas. No dia 3,
cada pessoa que recebeu a mensagem no dia 2 também
enviou a mesma para outras duas novas pessoas. E, assim,
sucessivamente. Se, do dia 1o até o final do dia 6 de
dezembro, 756 pessoas haviam recebido a mensagem, o
valor de x é:
a)
b)
c)
d)
e)
12
24
52
63
120
æ 1 1 ö
45. Quantos termos da P.G. ç1, , ,...÷ devem ser somados
è 2 4 ø
1.023
para que a soma resulte
?
512
5
46. (UCSal-BA) A soma dos infinitos termos da seqüência
æ1 1 1 1 ö
ç , 2 , 3 , 4 ...÷ é:
è3 3 3 3 ø
a)
b)
c)
d)
e)
5
8
1
2
1
3
zero
¥
53. (Cairu-BA) O preço de um determinado bem é
desvalorizado, anualmente, em 12%. Após três anos, o
percentual de desvalorização de um bem adquirido em
05 de janeiro de 1994 é, aproximadamente, igual a:
a) 68%
b) 32%
c) 31%
54. (UCSal-BA) Hoje, 50% da produção de uma fábrica de
sucos é de suco de caju e 50% é de suco de maracujá. Se a
produção de caju aumentar em 10% ao mês e a de suco de
maracujá aumentar em 20% ao mês, daqui a dois meses a
porcentagem de suco de maracujá produzido em relação ao
total produzido no mês será de, aproximadamente:
47. Um jardineiro quer dispor triangularmente as 1.830
árvores de um parque em fila, de sorte que a primeira fila
tenha uma árvore, a segunda duas, a terceira três e assim
por diante. Quantas filas terá a disposição?
48. (UFBA) Entre os marcos dos quilômetros 60 e 620 de
uma estrada, colocaram-se treze outros marcos
equidistantes entre si. Qual a distância, em km, entre o
quarto e o quinto marcos?
a) 72%
b) 60,5%
c) 57,3%
Barraca
Batata
Cenoura
A
R$ 1,30
R$ 1,00
B
R$ 1,50
............
Comprando a mesma quantidade, em quilos, de batata e
de cenoura na barraca A, gastaria R$ 6,90; comprando o
equivalente na barraca B, economizaria R$ 0,30. Assim
sendo, sobre o preço da cenoura nas duas barracas,
pode-se afirmar que:
1.024
24
4.096
12
16.777.216
50. Em uma PG de 7 termos, a soma dos dois primeiros é 8 e a
soma dos dois últimos é 1.944. A razão da progressão é:
a)
b)
c)
d)
e)
um número par, não-divisível por 4;
um número natural maior que 5;
um número irracional;
um número natural múltiplo de 3;
um número divisível por 4.
51. (UCSal-BA)
A
solução
da
equação
x +1 x +1 x +1
+
+
+ ... = 12 no universo R, é um
2
8
32
número:
a)
b)
c)
d)
e)
primo;
múltiplo de 3;
divisível por 5;
fracionário;
quadrado perfeito.
52. (UCSal-BA)
A
x x
x + + + ... < 3 é:
3 9
a)
b)
c)
d)
e)
x<1
x<2
x<3
x<4
x<5
d) 54,3%
e) 52%
55. (UEFS-BA) Uma dona de casa, tendo pesquisado os
preços de batata e de cenoura em duas barracas de uma
feira, verificou que os preços praticados, por quilo,
estavam de acordo com a tabela abaixo.
49. Uma bactéria de determinada espécie divide-se em duas a
cada 2 h. Depois de 24 h, qual será o número de bactérias
originadas de uma bactéria?
a)
b)
c)
d)
e)
d) 25%
e) 20%
solução
da
inequação
a)
b)
c)
d)
e)
em B, era 70% mais barata que em A;
em B, era 30% mais barata que em A;
em A, era 30% mais cara que em B;
em A, era 70% mais cara que em B;
em A e B, tinha o mesmo preço.
56. (Fuvest-SP) Sobre o preço de um carro importado incide
um imposto de importação de 30%. Em função disso, o
seu preço para o importador é de R$ 19.500,00. Supondo
que tal imposto passe de 30% para 60%, qual será, em
reais, o novo preço do carro para o importador?
a)
b)
c)
d)
e)
R$ 22.500,00
R$ 24.000,00
R$ 25.350,00
R$ 31.200,00
R$ 39.000,00
57. (Cairu-BA) Uma empresa distribui parte do seu lucro
entre suas três filiais. A primeira recebeu 30% da parte do
lucro mais R$ 3.000,00; a segunda, 35% da parte do lucro
mais R$ 5.000,00 e a terceira, 25% mais R$ 2.000,00.
A diferença entre os valores recebidos pela primeira e
terceira filiais, em reais, é igual a:
a)
b)
c)
d)
e)
6.000
7.000
8.000
10.000
12.000
6
58. (UCSal-BA) Em um certo país, as pessoas maiores de
21 anos pagam um imposto progressivo sobre os
rendimentos. Esse imposto corresponde a 10% sobre
as primeiras 1.000 unidades monetárias recebidas e
20% sobre os ganhos que ultrapassam esse valor.
Nessas condições, indicando por i o valor do imposto
e por r uma renda superior a 1.000, tem-se:
a) i = r – 100
b) i = 100 + 0,3 r
c) i = 0,3 r
d) i = 100 + 0,2 r
e) i = 0,2 r – 100
59. (UESB-BA) Numa pesquisa eleitoral em uma cidade
com 734.400 habitantes votantes, três chapas foram
apresentadas com o seguinte resultado: a chapa 1 obteve
30% das intenções de voto, a chapa 2, 183.600 votos e a
chapa m, o restante.
O número de habitantes comprometidos com a chapa
vencedora nessa pesquisa é:
a)
b)
c)
d)
e)
183.600
220.320
263.800
330.480
173.920
60. (UCSal-BA) Atualmente, está em vigor um imposto
(CPMF) sobre os débitos em conta corrente que
corresponde a 0,2% do valor do débito. Assim, se um
correntista emite um cheque de R$ 30.000,00, o valor
do imposto devido é:
a)
b)
c)
d)
e)
R$ 0,06
R$ 0,60
R$ 6,00
R$ 60,00
R$ 600,00
61. (UCSal-BA) Um empresário reservou R$ 3.300,00 para
repartir entre seus dez empregados, como abono natalino.
Dentre os dez empregados, há dois com função de
gerência. Cada um deles deverá receber 50% a mais que
cada um dos outros.
Nessas condições, a parte de cada gerente é:
a)
b)
c)
d)
e)
R$ 250,00
R$ 300,00
R$ 350,00
R$ 400,00
R$ 450,00
62. (UEFS-BA) Pesquisas revelam que 35% das mulheres
entre 15 e 55 anos tingem os cabelos, sendo que 60%
dessas mulheres os tingem de louro.
Se o percentual de mulheres entre 15 e 55 anos que
apresentam cabelos, tingidos ou não, de cor loura é igual
a 30%, então a porcentagem, nessa faixa etária, de louras
naturais, ou seja, que não tingem os cabelos, é igual a:
a)
b)
c)
d)
e)
7%
9%
15%
22%
25%
63. (Uneb-BA) Analisando-se a delegação olímpica de um
determinado país nas Olimpíadas, em Atlanta-96 e em
Sydney-2000, observou-se que, em Atlanta, a delegação
tinha 225 atletas, dos quais 20% eram mulheres; em
1
Sydney, a delegação foi reduzida em em relação à de
3
Atlanta, e o número de mulheres dobrou.
Assim sendo, pode-se concluir que o percentual de
homens na delegação de Sydney correspondeu a:
a)
b)
c)
d)
e)
30%
40%
50%
60%
70%
64. (FBDC-BA) Se x = 3,6 × 10–6 e y = 0,75 × 10–4, então x é
igual a:
a)
b)
c)
d)
e)
4,8% y
24% y
48% y
240% y
480% y
65. (FBDC-BA) Dos 240 alunos de uma escola, 55%
estudam inglês e 35% possuem carro.
Sabendo-se que 72 alunos que estudam inglês têm carro,
a porcentagem dos alunos que não estudam inglês e não
têm carro é igual a:
a)
b)
c)
d)
e)
10%
20%
30%
40%
50%
66. (UEFS-BA) Dos R$ 90,00 de mesada que um
adolescente recebe, ele tem uma despesa mensal fixa de
R$ 15,00 para o transporte. Este mês, além da despesa
fixa, ele teve outros gastos correspondentes a R$ 105,00,
e, por esse motivo, precisou tomar emprestados 20% da
mesada do irmão. Com base nessas informações, pode-se
concluir que a soma das mesadas dos dois irmãos
corresponde, em reais, a:
a) 250
b) 245
c) 240
d) 234
e) 230
67. (UEFS-BA) Uma lanchonete cobra R$ 3,00 por uma
pequena refeição e faz a seguinte promoção: o
consumidor que comprar 4 refeições leva mais uma de
graça. Um cliente levou 18 refeições e rateou o valor
pago por 18 pessoas.
Considerando-se a promoção em vigor, a cota que cabe
a cada um foi igual a:
a)
b)
c)
d)
e)
R$ 1,90
R$ 2,00
R$ 2,35
R$ 2,50
R$ 2,80
7
68. (Consultec-BA) Um automóvel, cujo preço à vista é R$
14.500,00, está sendo vendido com um desconto de
fábrica de R$ 2.000,00, seguido de um desconto de 10%
do revendedor.
A taxa total de descontos é igual a:
a)
b)
c)
d)
e)
20,21%
21,35%
22,41%
23,40%
24,16%
69. (FBDC-BA) O IMC (Índice de Massa Corpórea)
relaciona a massa (em quilogramas) e a altura (em
metros) de uma pessoa através da expressão:
massa
IMC =
(altura )2
Há algum tempo, Ambrosiana estava com massa
corpórea igual a 35 kg/m2, começou a fazer um programa
de redução alimentar e conseguiu uma redução de 40%
nesse índice. Considerando que Ambrosiana tem 1,70 m
de altura, então sua massa, em kg, após o término desse
programa, é:
a)
b)
c)
d)
e)
40,46
54,37
60,69
68,74
73,96
70. (UEFS-BA) Juliana e Carolina são vendedoras em uma
loja e ganham R$ 600,00 mais uma comissão de 5% sobre
suas vendas. Nesse mês, Juliana ganhou R$ 1.200,00 e
Carolina ganhou R$ 1.350,00. A porcentagem das vendas
de Carolina foi superior à de Juliana em:
a)
b)
c)
d)
e)
11%.
20%.
25%.
32%.
40%.
71. (Mackenzie-SP) O vértice da parábola y = x2 + kx + m
é o ponto V(– 1, – 4).
O valor de k + m é:
a)
b)
c)
d)
e)
74. (UCSal-BA) Determine o valor de k para os quais a
parábola de equação y = x2 – 6x + k não corta o eixo Ox.
a) k > 0
b) k < 0
c) k < 9
75. (Consultec-BA) Para que valores de m a seguinte
equação define função quadrática? y = (m + 1)x2 – x + 1?
76. (Unicamp-SP) Determine o valor de m de modo que o
gráfico da função y = x2 + mx + 8 – m seja tangente ao
eixo dos x.
a) – 8 e 4
b) 4 e 8
a) – 6
b) 6
c) 0
d) – 5
e) 5
78. O gráfico da função f(x) = x2 + bx + c, com b e c reais, tem
um único ponto em comum com o eixo das abscissas.
Então:
a) c = 0
b2
4
b
c) c =
2
b
d) c = 2
b2
e) c =
2
b) c =
79. (Uneb-BA) A reta e a parábola, representadas no gráfico,
têm equações iguais, respectivamente, a 2x – 3y + 12 = 0
2
4
16
e y = - x2 + x +
3
3
3
Da análise do gráfico, conclui-se que a área da região
sombreada mede, em u.a.:
–2
–1
0
1
2
73. (PUC-SP) O conjunto imagem da função f:
{(x, y) Î R ´ R | y = x2 – 3} é:
{y | y Î R e y ³ 3 }
{y | y Î R e y ³ – 3}
{y | y Î R e y £ 3}
{y | y Î R e y ³ 0}
{y | y Î R e y ³ 3}
d) 8 e 4
e) – 8 e – 4
77. (UCSal-BA) Se os pontos (0, 6), (2, 4) e (3, 0) pertencem
ao gráfico de y = ax2 + bx + c, então a + b + c é igual a:
72. (Consultec-BA) Para que valores de m a seguinte
equação define função quadrática y = x2m – 1 + 2x?
a)
b)
c)
d)
e)
d) k > 9
e) k = 1
a)
b)
c)
d)
e)
10
11
13
15
18
8
80. (ITA-SP) A função quadrática definida por
y = – 6x2 + mx + t é representada por uma parábola que
passa pelo ponto (– 1; 0) e cujo vértice é o ponto (2; a).
O valor de a é:
a) – 6
b) 24
c) 18
d) 30
e) 54
87. Sendo a e b as raízes da equação x2 + mx + 2 = 0, o valor
a b
de + é igual a:
b a
a) m2
b) m2 – 2
c)
81. (UFMG) O trinômio y = ax2 + bx + c está representado
na figura.
m2 - 4
2
d) 4m2 – 2
e) m2 – 8
88. A altura y, em metros, que um projétil atinge, em função
da distância x do ponto de lançamento, é fornecida pela
expressão dada por y = – 60 x2 + 360 x, onde x é dado
em quilômetros. A altura máxima atingida pelo projétil é:
a) 60 m
b) 180 m
c) 360 m
d) 520 m
e) 540 m
89. (FAAP-SP) Para uma viagem, foi fretado um avião
com 200 lugares. Cada pessoa deve pagar R$ 300,00
mais a taxa de R$ 6,00 para cada lugar que ficar vago.
A afirmativa correta é:
a)
b)
c)
d)
e)
a) Qual a receita arrecadada se comparecerem 150
pessoas para a viagem?
b) Qual a máxima receita que pode ser arrecadada nas
condições do problema?
a > 0, b > 0 e c < 0
a < 0, b < 0 e c < 0
a < 0, b > 0 e c < 0
a < 0, b > 0 e c > 0
a < 0, b < 0 e c > 0
82. (UCSal-BA) Os valores de m, para que o mínimo da
função f(x) = x2 + (m - 2)x + 4 - m seja 2, são:
a) – 1 e 3.
b) – 2 e 3.
c) – 2 e 2.
d) 0 e 2.
e) – 2 e 0.
90. (Fuvest-SP) Quero construir uma quadra de futebol de
salão retangular. Para cercá-la, disponho de 60 m de
alambrado pré-fabricado e, por uma questão de economia,
devo aproveitar o muro do quintal (veja figura). Quais
devem ser as dimensões dessa quadra para que sua área
seja máxima?
a) x = 20 m e y = 10 m
b) x = 15 m e y = 30 m
83. (UCSal-BA) Calcule m de modo que o máximo valor
do trinômio – x2 – 2mx – 5 seja o quádruplo do
correspondente valor de x.
c) x = 12 m e y = 18 m
d) x = 10 m e y = 10 m
e) x = 8 m e y = 30 m
2
84. Determine m para que a equação x + mx + 2 = 0 tenha
duas raízes, sendo uma o dobro da outra.
85. (Uneb-BA) Sabendo-se que o gráfico da função definida
por f(x) = x2 – 2x + k é uma parábola e que o menor valor
de f(x) é igual a 2k, então a soma das coordenadas do
vértice dessa parábola é:
a)
b)
c)
d)
e)
91. Dispõe-se de uma folha de papel retangular medindo
20 cm de largura por 24 cm de comprimento. Desejase recortar em cada quina da folha quatro quadrados
iguais (veja figura). Quanto deve medir o lado de cada
quadrado para que a área da região sombreada seja
máxima?
–4
–3
–1
0
1
86. (FBDC-BA) O gráfico da função f, do 2o grau, tem
como eixo de simetria a reta de equação x – 2 = 0. Se a
distância entre os pontos que representam as raízes da
função é de 6 unidades e a função assume valor máximo
igual a 18, então o valor de f(0) é:
a)
b)
c)
d)
e)
– 10
–5
0
5
10
a)
b)
c)
d)
e)
4,5 cm
5 cm
5,5 cm
6 cm
6,5 cm
9
92. Um grupo de estudantes de meteorologia pesquisa as
variações bruscas de temperatura numa certa cidade.
Após longa coleta de dados, conclui-se que, às t horas
da madrugada, a temperatura, em um determinado dia,
foi dada por C(t) = -
100.(Uneb-BA)
t2
+ 4t + 10, em graus Celsius.
6
Quanto aumentou ou diminuiu a temperatura, nesse dia,
entre 18 e 21 horas?
93. (Consultec-BA) O trinômio ax2 + bx + c é negativo,
"x, se:
a) a > 0 e D < 0
b) a < 0 e D > 0
Da análise do gráfico onde estão representadas as
funções f(x) = – x + 2 e g(x) = x2, pode-se concluir que
f (x )
o conjunto-solução da inequação
< 1 é:
g(x )
c) a > 0 e D > 0
d) a < 0 e D < 0
94. (Consultec-BA) Se uma equação da forma ax2 + bx + c = 0,
a ¹ 0, apresenta raízes reais de sinais contrários, então:
a) c / a > 0
b) – b / a > 0
a) ]– 2, 1[ – {0}
b) ]– 1, 2[ – {0}
c) R – [– 1, 1]
101.O conjunto solução da equação |3x – 2| = 3x – 2 é:
c) c / a < 0
é2
é
a) ê ;+¥ ê
3
ë
ë
d) a / b > 0
95. Determine o domínio da seguinte função:
b) R+
ù2
é
d) ú ;+¥ ê
û3
ë
c) R
2ù
ù
e) ú - ¥; ú
3û
û
y = x (x - 5)
96. Determine o domínio da seguinte função:
y=
x-2
x+4
97. (PUC-SP) Os valores de m Î R, para os quais o domínio
1
da função f(x) =
é R, são:
2
2 x - mx + m
a) 0 < m < 8
b) m > 10
c) m > 0
d) 1 < m < 2
e) 0 £ m £ 7
98. (PUC-MG) A função quadrática f(x) = mx2 + 2(m – 2)x
+ m é positiva para qualquer valor real de x se:
a) m ¹ 0
b) 0 < m < 1
c) m > 0
d) m >
d) R – [– 1, 2]
e) R – [– 2, 1]
1
4
e) m > 1
99. Determine m de modo que, para qualquer que seja o
valor real de x, ocorra mx2 + 4(m – 1)x + m – 1 > 0.
102.(ESPM-SP) Sabendo que |x|2 = x2, resolver a equação:
x2 – 5 × |x| + 6 = 0
103.(UEL-PR) No universo R, a equação |x|2 + |x| – 12 = 0:
a)
b)
c)
d)
e)
não admite soluções;
admite quatro soluções distintas;
admite duas soluções positivas;
admite duas soluções negativas;
admite duas soluções opostas entre si.
104.(Aman-RJ) O domínio de x em |x – 5| < 3 é:
a) não existe
b) 2 £ x £ 8
c) 2 < x < 8
d) x < 2 ou x > 8
e) x £ 2 ou x ³ 8
105.(PUC-SP) O número de soluções da equação ||x| – 1| = 1,
no universo R, é:
a)
b)
c)
d)
e)
0
1
2
3
4
10
GABARITO
0
6
7
8
0
1
– B 05 B C B D
B 32 E 04 D 26 D
C
D
B D
D 24
2
B
6
B 30 45 04 A
D
A
A
3
B
B
C
E
E
C
A
D
4
B
E
D
A
A 10 B 60 40 C
5
D
A
B
B
D
B
B
A
E
D
6
D
E
B
B
A
D C
D
C
C
7
C
B
B
D
B
B
C
E
B
C
E
¯
B
C
¯
¯
C
E
9
¯
D
¯
C
A
8
¯
C
¯
A
E
10 05 A
¯
E
C
¯
D
¯
¯
¯
¯
D
72. m =
1
2
3
3
2
75. m ¹ – 1
83. m = 1 ou m = – 5
84. m = ± 3
89. a) 90 000
b) 93 750
92. diminuiu 7,5oC
95. ]– ¥; 0] È [5; + ¥[
96. ]– ¥; – 4[ È [2; + ¥[
ù 4é
99. ú1; ê
û 3ë
102.{– 3, – 2, 2, 3}
4
5
A
C
9
RESOLUÇÃO COMENTADA - LISTA 05
01.
6a 3 = 4374
a 3 = 729
a =9m
2p
face
= 4.a = 4.9 = 36 m
02.
Vmaterial = Vbloco - 6.Vfuro
Vmaterial = 10 3.10 3.15 - 6.x.x.15
Vmaterial = 4500 - 90x
2
Vmaterial = 90æç 50 - x 2 ö÷
è
03.
ø
V = Sb.h
l2 3
.h
4
1 2
2 3
V=
.2
4
V=
V = 2 3 m3
04.
3
a6 = l
2
Sl = 2 p
3
3 3= l
2
Sl = 6.6.10
l = 6 cm
Sl = 360 cm 2
base
.h
05.
2 Sb + Sl = 110 ®ì
ï2ℓ + 4ℓ h = 110
í
3
3 2
AFACE = s b ® ïℓ h = ℓ
5
î
5
3
2ℓ 2 + 4. ℓ 2 = 110
5
2
V = Sb.h
ℓ 2 = 25
V = 5 2 .3
ℓ =5m
V = 75 m 3
3
5.h = .5 2
5
h = 3m
06.
d=a 2
5 2 =a 2
a =5
V = a 3 = 5 3 = 125 u.v.
12
07.
12a = 60
a =5m
D=a 3 =5 3m
08.
S T = 72
D=a 3
6a 2 = 72
D = 2 3. 3
a 2 = 12
D = 6m
a=2 3m
09.
6a 2 = 96
V = a' 3
a 2 = 16
216 = a' 3
a = 4m
a' = 3 216 '
a' = 6 m
Logo, a aresta deve aumentar em 2 m.
10.
cosα =
a
=
a 3
1
3
a 3
11. Chamando de x o número de cubos a ser colocado em cada aresta, temos:
x 3 + 5 = (x + 1)3 - 32
x 3 + 5 = x 3 + 3x 2 + 3x + 1 - 32
2
3x + 3x - 36 = 0 (¸3)
x 2 + x - 12 = 0
x 1 = -4 (Não convém )
x2 = 3
Portanto, o número total de cubos é 33 + 5 = 32.
12.
d 2 = (2a )2 + a 2
d 2 = 5a 2 ® d = a 5
13
13.
V = 13 = 1 m 3 = 1000 dm 3 = 1000l
1000l - 100%
10l - x
1000x = 1000%
x = 1% =
1
100
= 10 - 2
14.
A secção = 6
V = a3
a.a 2 = 6
V=
a2 =
V = 4 27 m 3
3
( 3)
3
4
a=43m
15.
æx + y + z = 8 ® x + y = 8 - z
ç
ç 2x + y + z = 9
ç z + 3(x + y ) = 16
è
ìx + y + 4 = 8
í
z + 3(8 - z ) = 16
î2x + y + 4 = 9
z + 24 - 3z = 16
2z = 8
x =1
y=3
z=4
2
2
2
d =x +y +z
2
d 2 = 12 + 3 2 + 4 2
d 2 = 26
16.
SB
V = S B .h = 34.14.8 = 3808 cm 3
17.
V = a.b.c
60 = 3.5.c
c = 4m
D2 = a 2 + b2 + c2
D
4
3
5
D = 50
D=5 2m
14
18.
22a 2 = 198
a2 = 9
a = 3 cm
V = a 3 = 33 = 27 cm 3
19.
ì 13
ì 13
ïïh = 10 r
ïïh = 10 r
®
í
í
ï 1 (h + 2r ) = 16,5 ïr = 16,5 - h
îï 2
îï
2
h=
13 æ
hö
ç16,5 - ÷
10 è
2ø
h = 13 m
r = 10 m
Sl CIL = 2.p .10.13 = 260π cm 2
26 2 = 10 2 + H 2
260π = π.10.g
g = 26
H
26
H = 576
H = 24 m
10
20.
a 3 = 64
4
2
4
2
VCIL = π r .h
y π = π.2 2 .4
y = 16
21.
2
6a = 2π r h
6.2 2 = 2p .2.h
h=
6
π
x=6
m
4
a = 4 cm
15
22.
0,8 mm = 0,08 cm
VPEDRA = VÁGUA DESLOCADA = π.20 2 .0,08 = 32π cm 3
VPEDRA @ 32.3,14 @ 100,5 cm 3
23.
(01) FALSA.
Sb =
l2 3
4
=
(1,2)2
3
4
= 0,36 3 m 2
(02) VERDADEIRA
(04) VERDADEIRA
Sl = 2p.h = 3.1, 2.1, 8 = 6,48 m 2 = 648 dm 2
(08) VERDADEIRA
l=R 3
V = Sb.h = 0,36 3.1,8 = 0,648 3 m 3 = 648 3 dm 3
®R=
1,2 = R 3
(16) VERDADEIRA
l
=
a
(64) FALSA
3
.
3
3
R = 0,4 3 m
Como o prisma e a pirâmide têm base e altura iguais, então :
VPIRÂMIDE =
(32) FALSA
1,2
1
V
® VPRISMA = 3.VPIRÂMIDE.
3 PRISMA
l
l
l
6
3
=
=
=
.
=2 3
h
l 3
l 3
3 3
3
2
6
3
A• = 0,36 3
L2 = 0,36 3
L = 0,36 3
L = 0,6 4 3 m
24.
d= 6
l4 2 = 6
l4 = 3 m
3
3
l
2
2
2
æ l ö æç 3 ö÷
l =ç ÷ +
è 2 ø çè 2 ÷ø
2
3l 2
4
l
2
4
l =1m
V=
2
3
=
V=
6.12 3
4
9
2
. 3
3
m =x
10x = 10.
9
2
= 45
2
16
25.
VCIL
VCUB
VCIL
VCUB
=
=
π.r 2 .h
a3
π.r 2 .2 r
=
(2 r )3
=
2 π r3
8 r3
π
4
26.
V = π.5 2 .30
30 cm
V = 750π @ 2355 cm 3
V = 2,355 l
Logo, colocando -se 2 l de água no cano, a água ultrapassa o meio do cano.
10 cm
27.
C1 = 2 π R 1
C2 = 2 π R 2
6 = 2 π R1
4 = 2 π R2
R1 =
3
R2 =
π
2
æ3ö
V1 = π.ç ÷ .4 π
èπø
V1 = 36
2
π
2
æ2ö
V2 = π.ç ÷ .6π
èπø
V2 = 24
Logo, 2 V1 = 3 V2
28.
St 1 = Sl 2
2 π r 2 + 2 π r. 20 = 2 π (r + 5).20
r 2 +20 r = 20 r + 100
r = 10
29.
V = π.3 2 .10
V = 90π m 3
90π m 3
5h
x
1h
x=
90π
5
m 3 = 18π m 3
17
30.
ìïπ r 2 .h = L + 2 ®
í
ïî2π r.h = L
®
r.
L
2
r=
ìπ.r.r.h = L + 2
ï
í
L
ïîπ r h = 2
=L+2
2
L
.(L + 2 )
31.
Sl 1 = Sl 2
V1
2π R 1 H1 = 2π R 2 H 2
V2
R 1H1 = R 2 H 2
=
π R 12 H1
π R 22 H 2
=
R 1 .R 1 .H 1
R 2 .R 2 .H 2
=
R 1 .R 2 .H 2
R 2 .R 2 .H 2
32.
1m
1m
50 m
0,04 m
1m
Vcil = π.(0,02)2 .50 @ 0,06 m 3
Vcubo = 13 = 1 m 3
Após o cilindro encher de água :
V' cubo = Vcubo - Vcil = 1 - 0,06 = 0,94 m 3
V' cubo = 1.1.h' ® 0,94 = 1.1.h' ® h' = 0,94 m
h' = 94 cm
B
33.
B
A
5
C
BC
B
A
ht
h = 10 dm
h=
10
45
º
O
O
O
45º
R = 5 dm
5
B
A
45º
O ΔBC é retângulo e isósceles, logo AB = BC = 5
h = hf + BC ® 10 = hf + 5 ® hf = 5
V = A base .h ® V = π.r 2 .hf ® V = (3,14 ) . 5 2 . 5
º
45
C
V = 392,5 dm 3
=
R1
R2
18
34.
A = 90
4 2 = 32 + 4 2
15.x = 90
y= 7m
x=6
4- 7
3
3
y
7
4
4
(
)
(
)
d = 4 + 7 m ou 4 - 7 m
35.
2x + 1
4x
x -1
=
2x + 1
2
4x - 4x = 4x 2 + 2x + 2x + 1
- 8x = 1
x=-
1
8
36.
x+9
=
x
x + 45
x+9
2
x + 9x + 9x + 81 = x 2 + 45x
27x = 81
x=3
a1 = 3
q=
a 2 = 12
37.
a 8 = a 1 .q
7
æ1ö
= a 1 .ç ÷
2
è2ø
1
1
2
=
7
a1
2
a1 =
7
27
= 26
2
38.
a 5 = a 1 .q 4
324 = 4.q 4
4
q = 81
q=3
12
3
=4
19
39.
(..., a 5 , a 6 , a 7, ... ) P.G.
a 62 = a 5 .a 7
a 6 = 10.16
a 6 = 4 10
40.
æ 6
ö
çç ..., , 6, 6q, ... ÷÷ P.G.
è q
ø
6
q
+ 6 + 6q = 26
6 + 6q + 6q 2 = 26q
6q 2 - 20q + 6 = 0 ( ¸2 )
2
3q - 10q + 3 = 0
Δ = 100 - 36
Δ = 64
q=
10 ± 8
6
6q = 6.3 = 18
q1 = 3
ou
1
q 2 = (Não convém )
3
41.
x
æ
ö
, x 1 , - 3x, ... ÷ P.G.
ç ...,
è -3
ø
x
-3
.x.(- 3x ) = 216
x 3 = 216
a 5 = a 1.q 4
a 5 = -2.(- 3)4
a 5 = -162
x=6
42.
ìa + a .q 2 = 5
ìa 1+ a 3 = 5
ï 1 1
®í
í
îa 2 + a 4 = 10 ïîa 1 .q + a 1 .q 3 = 10
q æç a 1 + a 1 .q 2 ö÷ = 10
è
ø
q . 5 = 10
a 4 = a 1 .q 3
q=2
a 4 = 1.2 3
a 1 + a 1 .2 2 = 5
a4 = 8
a1 = 1
20
43.
a 1 æç q11 - 1ö÷
è
S11 =
ø
q -1
3 0 æç 311 - 1ö÷
è
S11 =
ø
3 -1
11
3
S11 =
-1
2
44.
S6 =
a 1 æç q 6 - 1ö÷
è
ø
q -1
x æç 2 6 - 1ö÷
è
756 =
ø
2 -1
756 = x . 63
x = 12
45.
Sn =
a 1 æç q n -1ö÷
è
ø
q -1
é 1
ù
æ ö
1êç ÷ - 1ú
êè 2 ø
ú
n
1023
512
=
ë
û
1
2
-1
n
1023
512
-
=
æ1ö
ç ÷ -1
è2ø
1
-
2
n
æ1ö
= ç ÷ -1
1024 è 2 ø
1023
æ1ö
=ç ÷
1024 è 2 ø
1
2 -10 = 2 - n
n
n = 10
46.
1
S¥ =
a1
1- q
=
1
1
= 3 =
1 2 2
13 3
3
21
47.
Sn =
(a 1 + a n ). n
1830 =
2
(a 1 + a 1 + (n - 1) R ). n
2
3660 = (1 + 1 + n - 1).n
3660 = n + n 2
n 2 + n - 3660 = 0
n 1 = 60 ou n 2 = -61
(Não convém)
48.
(a 1 , ..., ..., ..., ..., a 15 ) P.A.
a 15 = a 1 + 14 R
620 = 60 + 14 R
14 R = 560
R = 40
49.
a 13 = a 1 .q 12
a 13 = 1.212
a 13 = 4096
50.
ìïa 1 + a 1 .q = 8
ìa 1 + a 2 = 8
®í
í
îa 6 + a 7 = 1944 ïîa 1 .q 5 + a 1 .q 6 = 1944
q 5 (a 1 + a 1 .q ) = 1944
q 5 .8 = 1944
q 5 = 243
q=3
Logo, a razão é um número natural múltiplo de 3.
51.
S¥ =
a1
1- q
9=
x +1
2
x +1
2
12 =
112.
3
4
=
1
4
x +1
2
x = 17
Logo, x é um número primo.
22
52.
S¥ >
a1
x
3>
13.
x<2
1- q
2
3
1
3
>x
53.
P = Po (1 - i )n
P = Po (1 - 0,12)3
P = Po (0,88)3
P @ 0,68 Po
Logo, a desvalorização é de aproximadamente 32%.
54.
Supondo que a produção de suco seja de 100 l :
caju : 50 (1 + 0,1)2 = 60,5 l
maracujá : 50 (1 + 0,2)2 = 72 l
72
132,5
@ 0,543 @ 54,3%
55.
1,3 n + 1 n = 6,9ü
2,3 n = 6,9
n = 3 kg
ï
ý Barraca A
ï
þ
1,5.3 + x. 3 = 6,6ü
3x = 2.1
x = 0,70
ï
ý Barraca B
ï
þ
Logo, o preço da cenoura na Barraca B era 30% mais barato do que na Barraca A.
56.
p = p o (1 + i )
19500 = p o (1 + 0,3)
p o = 15000
p' = p o (1 + i')
p' = 15000 (1 + 0,6 )
p' = 24000,00
23
57.
Sendo x a parte do lucro: :
0,3x + 3 000 + 0,35x + 5 000 + 0,25x + 2 000 = x
0,1x = 10 000
x = 100 000,00
1a Filial :
3 a Filial :
30
100
25
.100 000 + 3 000 = 33 000,00
100
.100 000 + 2 000 = 27 000,00
Diferença
58.
= 6 000,00
10%.1000 = 100
20%.r = 0,2 r
i = 0,2 r - 100
59.
Chapa 1 : 30% . 734 400 = 220 320 votos
Chapa 2 :183 600 votos
Chapa 3 : 734400 - 403 920 = 330 480 votos
Logo, a chapa 3 foi a vencedora, com 330 480 votos.
60.
I = 30.000.0,2% = 60,00
61.
8.1x + 2.1,5x = 3300
11x = 3300
x = 300,00
1,5.300 = 450,00
62.
Tingem o cabelo de louro
60
35
= 0,21 = 21%
100 100
Se 30% das mulheres têm cabelo louro, e dessas, 21% têm cabelo tingido, então 9% não tingem o cabelo.
.
63.
· Mulheres em Atlanta : 20% . 225 = 45
1
· Delegação em Sydney : 225 - .225 = 150
3
· Mulheres em Sydney : 2.45 = 90
· Homens em Sydney :150 - 90 = 60
60
150
= 0,4 = 40%
64.
x
y
=
3,6 . 10 - 6
0,75.10 - 4
= 4,8.10
-2
= 4,8%
24
65.
Inglês : 55% . 240 = 132
Carro : 35% . 240 = 84
60 + 72 + 12 + x = 240
x = 96
96
240
= 0,4 = 40%
66.
· Despesa do adolescente :120,00
· Empréstimo :120,00 - 90,00 = 30,00
30 - 20%
x - 100%
x=
30.100
= 150,00
20
Soma das mesadas : 90,00 + 150,00 = 240,00
67.
Como ele levou 18 refeições, então pagou apenas 15.
15.3 = 45,00
45,00
18
= 2,50
68.
14500 - 2000 = 12500,00
12500.0,9 = 11250,00
Logo, o desconto foi de 14500 - 11250 = 3250,00
3250
14500
@ 0,2241 = 22,41%
69.
0,6.35 = 21 kg/m 2
21 =
m
(1,7 )2
m = 60,69 kg
25
70.
· Juliana :1200 = 600 + 0,05x
x = 12 000, 00
· Carolina :1350 = 600 + 0,05y
y = 15 000, 00
12 000
100%
15 000
k=
k
15 .100%
12
k = 125%
Logo, a porcentagem foi superior em 25%.
71.
x v = -1
-4k
2.1
k=2
= -1
y v = -4
- æç 2 2 - 4.1.m ö÷
è
ø
= -4
4 .1
4 - 4m = 16
- 4m = 12
m = -3
k + m = 2 + (- 3) = -1
72.
2m - 1 = 2
m=
73.
3
2
Como a > 0, Im = {y Î R/y ³ y v }
yv = -
Δ
æç 0 2 - 4 . 1 (- 3)ö÷
è
ø
=4a
4. 1
y v = -3
Im = {y Î R/y ³ -3}
74.
Δ<0
(- 6)2 - 4 (1) .k < 0
36 - 4 k < 0
36 < 4 k
k >9
75.
m +1¹ 0
m ¹ -1
26
76.
Δ=0
m 2 - 4 (1) (8 - m ) = 0
2
m - 32 + 4m = 0
m 2 + 4m - 32 = 0
m1 = -8 ou m 2 = 4
77.
6 = a.(0 )2 + b.0 + c
c=6
ì- 2a - b = 1
+
í
î3a + b = -2
a = -1
4 = a.2 + b.2 + 6
3 (- 1) + b = -2
4a + 2b = -2
b =1
2a + b = -1 (I)
a + b + c = -1 + 1 + 6 = 6
2
0 = a.3 2 + b.3 + 6
9a + 3b = -6
3a + b = -2 (II)
78.
Δ=0
b 2 - 4.1.c = 0
2
b - 4c = 0
b 2 = 4c
c=
b2
4
79.
2x + 12
ì
ïy =
3
ï
í
- 2x 2 + 4x + 16
ï
y
=
ïî
3
2x + 12
3
=
- 2x 2 + 4x + 16
y1 =
2 (2 ) + 12
=
16
3
3
2 (- 1) + 12 10
y2 =
=
3
3
No trapézio hachurado :
3
2x 2 - 2x - 4 = 0 (- 2 )
B = 16
x2 - x - 2 = 0
b = 10
x 1 = 2 ou x 2 = -1
h =3
3
æ 16 10 ö
ç + ÷.3
è3 3ø
A=
2
3
A = 13 u.a.
27
80.
0 = -6 (- 1)2 + m (- 1) + t
2
y = -6x + 24x + 30
- æç 24 2 - 4. (- 6 ). 30 ö÷
m - t = -6 (I )
yv =
è
4.(- 6 )
xv = 2
-m
2 (- 6 )
=2
m = 24
a=
- 1296
- 24
a = 54
24 - t = -6
t = 30
81.
a<0
b<0
c<0
82.
yv = 2
- é(m - 2 )2 - 4.1 (4 - m )ù
êë
úû
=2
4.1
2
m - 12 = -8
m2 = 4
m = ±2
83.
y v = 4.x v
-Δ 2 æ- bö
= 4.ç
÷
4a
è 2a ø
- é(- 2m )2 - 4. (- 1) (- 5)ù
êë
úû
4 (- 1)
- 4m 2 + 20
-4
æ 2m ö
÷
è -1 ø
= 2.ç
= -4m
m 2 + 4m - 5 = 0
m 1 = -5
ou
m2 =1
84.
ìx 1 = 2x 2
ï
í
ïîx 1 .x 2 = 2
2x 2 .x 2 = 2
x 22 = 1
x 2 = ±1
x1 = ± 2
x1 + x 2 =
-m
1
1 + 2 = -m ®
m = -3
ou
ou
- 1 + (- 2 ) = - m ® m = 3
ø
28
85.
y v = 2k
- (4 - 4k )
= 2k
4
- 1 + k = 2k
k = -1
86.
ìb = -4a (I)
ïï
ía - b + c = 0 (II)
ï 2
ïî- b + 4ac - 72a = 0 (III)
· xv - 2 = 0
xv = 2
SUBST. (I) em (II):
-b
a - ( -4a) + c = 0
2a
= 2 ® b = -4a
c = -5a (IV)
SUBST. (I) e (IV) em (III):
2
x1 = -1
x2 = 5
- (- 4a )2 +4a (- 5a )- 72a = 0
2
x1 = -1 ® 0 = a (- 1)2 + b (- 1) + c
a-b+c=0
· y v = 18
-Δ
4a
a (a + 2 )= 0
= 18
a =0
ø = 18 ® - b 2 + 4 a c = 72a
4a
- b 2 + 4 a c - 72a = 0
87.
ìa + b = - m ® (a + b )2 = (- m )2
ï
í
ïîa . b = 2
a 2 + 2 ab + b 2 = m 2
a 2 + b 2 = m 2 - 2 ab
a 2 + b2 = m2 - 4
b
b
a
=
a2 + b2
ab
=
m2 - 4
2
88.
- æç 360 2 - 4.(- 60).0 ö÷
yv =
yv =
è
- 36a 2 - 72a = 0 ( ¸ - 36 )
2
è
+
- 36a 2 - 72a = 0
a + 2a = 0
- æç b 2 - 4 a c ö÷
a
2
-16a - 20a - 72a = 0
6 u.c.
4.(- 60)
- 129600
- 240
y v = 540 m
ø
ou
a = -2
(Não convém)
Logo, b = 8 e c = 10.
f(x) = - 2x 2 + 8x +10
f(0) = -2 (0) 2 + 8 (0 ) + 10 ® f(0) = 10
29
89.
ì2x + y = 60 ® y = 60 - 2x
í
îA = x.y
A = x (60 - 2x )
A = -2x 2 + 60x
xv =
- 60
= 15 m
-4
y v = 60 - 2.15 = 30 m
90.
ì y + 2x = 60 ® y = 60 - 2x
í
îA = x.y
A = x (60 - 2x )
A = -2x 2 + 60x
xv =
- 60
2 (- 2 )
= 15 m
y v = 60 - 2.15
y v = 30 m
91.
A somb = 2.[(24 - 2x ).x ] + 2.[(20 - 2x ).x ]
A somb = 2 æç 24x - 2x 2 ö÷ + 2 æç 20x - 2x 2 ö÷
è
ø
è
ø
2
A somb = -8x + 88x
x máx = x v =
-b
2a
=
- 88
2 (- 8)
= 5,5 cm
92
xv =
-4
= 12
C (18) = -
æ 1ö
2 ç- ÷
è 6 øC
18 2
6
+ 4.18 + 10
C (18) = 28°C
C (21) = t
12
Logo, de t = 18 a t = 21, a temperatura diminui.
93.
a<0
e
Δ<0
C (21)
212
+ 4.21 + 10
6
= 20,5°C
Logo, diminui 28°C - 20,5°C = 7,5°C
30
94.
OU
x1
x2
x1
x2
a > 0 e c < 0 ou a < 0 e c > 0
Logo, c < 0.
a
95.
x.(x - 5) ³ 0
x 2 - 5x ³ 0
x = 0 ou x = 5
D =] - ¥, 0] È [5; ¥ [
96.
x-2
-4
³0
x+4
x-2=0
x+4¹0
x=2
x ¹ -4
-
+
D = ] - ¥, - 4 [ È [ 2; ¥ [
2
97.
2x 2 - mx + m > 0
isso ocorre para a > 0 e Δ < 0.
Como a = 2 > 0, façamos Δ < 0.
Δ = (- m )2 - 4 (2 )(m ) < 0
m 2 - 8m < 0
m 2 - 8m = 0
m (m - 8) = 0
2
+
+
0
ou
m1 = 0
m2 = 8
Logo, 0 < m < 8.
8
31
98.
a > 0eΔ < 0
m>0
Δ = [2 (m - 2 )]2 - 4.m.m < 0
m > 0em >1
4 æç m 2 - 4m + 4 ö÷ - 4m 2 < 0
Logo, m > 1.
è
ø
4m 2 - 16m + 16 - 4m 2 < 0
- 16m < -16
m >1
99.
m > 0eΔ < 0
[4 (m - 1)]2 - 4.m (m - 1) < 0
12m 2 - 28m + 16 < 0 ( ¸ 4)
3m 2 - 7m + 4 < 0
+
Δ = 49 - 48 = 1
7 ±1
m=
+
1
4
4
m1 =
ou 3
m2 = 1
6
3
S = ] 1; 4 [
3
100.
-x+2
2
x
-x+2
x
2
<1
0
1
-1< 0
- x + 2 - x2
x2
-2
<0
2
2
-x -x+2=0
x ¹0
x 1 = -2 ou x 2 = 1
x¹0
S = R - [ -2; 1]
+
+
0
101.
Como o “modulando” é igual ao segundo membro, qualquer valor de x satisfaz a igualdade, desde que esse valor
pertença à condição de existência do 2o membro.
2
é2
é
3x - 2 ³ 0 ® x ³
S = ê ;¥ ê
3
ë3
ë
32
102.
Δ = (- 5)2 - 4.1 (6 ) = 1
x =
5 ±1
2
x = 3 ou x = 2
x = ± 3 ou x = ± 2
103.
Δ = 12 - 4.1 (- 12) = 49
x =
-1± 7
x =3
x =±3
104.
2
ou
x - 5 < 3 e x - 5 > -3
x <8e x > 2
D = {X Î R / 2 < n < 8}
105.
x - 1 = 1 ou x - 1 = -1
x = 2 ou x = 0
x = ± 2 ou x = 0
Logo, a equação possui 3 soluções reais.