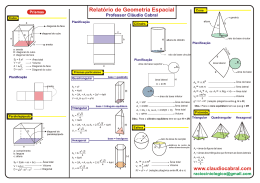
GEOMETRIA ESPACIAL
Triângulo equilátero
CUBO
Considere um cubo de aresta a:
ÁREA
√
ALTURA
√
ÁREA TOTAL
DIAGONAL
√
VOLUME
√
APÓTEMA
Hexágono regular
PARALELEPÍPEDO
Um hexágono pode ser dividido em 6 triângulo
equiláteros. Assim, a sua área equivale à área de 6
triângulos equiláteros e sua apótema corresponde à
altura do triângulo equilátero.
ÁREA TOTAL
DIAGONAL
√
ÁREA
√
VOLUME
APÓTEMA
√
PRISMAS
CILINDRO
Considere um cilindro reto de raio r e altura h.
ÁREA LATERAL
ÁREA TOTAL
VOLUME
A área lateral é igual à
área das faces.
A área total é igual à
soma da área lateral com
o dobro da área da base.
É o produto da área da
base pela altura do
prisma.
ÁREA LATERAL
ÁREA DA BASE
ÁREA TOTAL
VOLUME
Cilindro equilátero: h = 2r
PIRÂMIDE
CONE
Considere um cone de raio r, altura h e geratriz g.
Considere uma pirâmide de aresta lateral a, aresta
da base , altura h, apótema da base ab e apótema
lateral ap, com n lados.
RELAÇÃO ENTRE
APÓTEMAS E
ALTURA
ÁREA LATERAL
ÁREA LATERAL
ÁREA TOTAL
(
)
VOLUME
ÁREA TOTAL
SETOR CIRCULAR
Cone equilátero: g = 2r.
VOLUME
Tetraedro
Considere um tetraedro de aresta igual a .
ALTURA
√
√
ÁREA LATERAL
√
ÁREA TOTAL
VOLUME
√
√
Octaedro
Considere um octaedro de aresta igual a .
ALTURA
√
ÁREA TOTAL
VOLUME
RELAÇÃO ENTRE
RAIO, ALTURA E
GERATRIZ
√
√