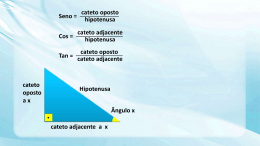
atemática
ES
SUAS
UAS TEC
CNO
NOLO
OG
GI A
AS
S
Ficha de Estudo
42
Tema
Atuando no dia a dia da Sociedade
Tópico de estudo
Triângulo Retângulo: Razões Trigonométricas e Relações Métricas
Entendendo a competência
Competência 3 – (Construir noções de grandezas e medidas para a compreensão da realidade e a solução de problemas do cotidiano).
Refere-se à capacidade de identificar as grandezas (tudo que pode ser medido), entender seu papel de descrever
quantitativa e qualitativamente os fenômenos, fazer cálculos de medidas e usá-los na representação da realidade, na
construção de argumentos e na solução de problemas do cotidiano.
Desvendando a habilidade
Habilidade 12 – (Resolver situação-problema que envolva medidas de grandezas).
Significa saber utilizar a noção de grandezas e suas medidas na resolução de problemas do cotidiano. Medir áreas e
perímetros de terrenos, volumes de recipientes, alturas de construções são práticas comuns em nosso dia a dia que
requerem identificação de grandezas, conhecimento de unidades de medidas relacionadas a essas grandezas e suas
conversões, além de prática em métodos geométricos.
© Delfim Martins/Pulsar Imagens
Situações-problema e conceitos básicos
Medindo Grandes Alturas
O teodolito é um instrumento ótico muito usado em topografia na
medição de grandes distâncias e alturas. É constituída por uma luneta,
apoiada em um tripé, que permite que um observador, situado em um
ponto P, aponte-a para um referencial R para que o teodolito forneça o
ângulo agudo ! que o segmento PR faz com o plano horizontal.
Um topógrafo decidiu calcular a altura de uma montanha com o auxílio de um teodolito, procedendo da seguinte forma:
1a Medição: Instalou o teodolito em um ponto A do solo e o apontou
para um ponto P no alto da montanha, obtendo um ângulo de 45".
2a Medição: Aproximou-se 170 m da montanha, fixou novamente o teodolito e mirou novamente no ponto P, obtendo agora um ângulo de 60".
Curso Pré-ENEM
Matemática
Com esses valores, como o topógrafo pode calcular a altura desejada?
Para resolver esse problema, vale lembrar das RAZÕES TRIGONOMÉTRICAS em um triângulo retângulo.
a: hipotenusa
b: cateto oposto ao ângulo !
c: cateto adjacente ao ângulo !
RAZÕES TRIGONOMÉTRICAS:
sen ! 5
cateto oposto ao ângulo !
b
5
hipotenusa
a
cos ! 5
cateto adjacente ao ângulo !
c
5
hipotenusa
a
tg ! 5
cateto oposto ao ângulo !
b
sen !
5 5
cateto adjacente ao ângulo !
c
cos !
Relação Fundamental: sen2 ! 1 cos2 ! 5 1
RAZÕES TRIGONOMÉTRICAS NOTÁVEIS:
sen
cos
tg
30°
1
2
3
2
3
3
45°
2
2
2
2
1
60°
3
2
1
2
3
Aproveitando que o assunto é o triângulo retângulo, vamos fazer uma revisão de algumas relações métricas
importantes válidas neste tipo de polígono:
a: hipotenusa
b, c: catetos
h: altura relativa à hipotenusa
m, n: projeções ortogonais dos catetos sobre a hipotenusa
b?c5a?h
; b2 5 a ? m ; c2 5 a ? n
; h2 5 m ? n
Teorema de Pitágoras: a2 5 b2 1 c2
Voltando à medição da altura da montanha, o topógrafo utiliza os dados fornecidos pelo teodolito da seguinte
forma:
tg 60" 5 H 5 3 # x 5 H 3
x
3
tg 45" 5
H
5 1 # x 5 H 2 170
x 1 170
# H 2 170 5 H 3 #
3
510
H5
5 510(3 1 3 ) 5 85(3 1 3 ) > 402,5 m
32 3
6
Curso Pré-ENEM
Matemática