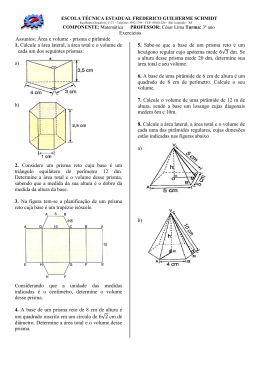
LISTA DE EXERCÍCIOS
Goiânia, ____ de ___________ de 2014
Série: 3ª Série
 Turma: _____
Aluno(a):______________________________________________________________
Disciplina: Matemática  Professor: JR  e-mail: [email protected]
Bloco Retangulares
1. (UNICAMP) Responsável por 20% dos acidentes, o uso de pneu
“careca” é considerado falta grave e o condutor recebe punição de 5
pontos na carteira de habilitação. A borracha do pneu, entre outros
materiais, é constituída por um polímero de isopreno (C5H8) e tem uma
densidade igual a 0,92 g cm–3. Considere que o desgaste médio de um
pneu até o momento de sua troca corresponda ao consumo de 31 mols
de isopreno e que a manta que forma a banda de rodagem desse pneu
seja um retângulo de 20 cm × 190 cm. Para esse caso específico, a
espessura gasta do pneu seria de, aproximadamente,
a) 0,55 cm.
b) 0,51 cm.
c) 0,75 cm.
d) 0,60 cm.
Dados de massas molares em g mol–1 : C=12 e H =1.
2.
(UNIMONTES) Um tanque tem a forma de um paralelepípedo
reto de dimensões 3m, 3m e 10m. Para enchê-lo de água, são
necessárias 5 horas. Esse tanque recebe água à razão de
a) 30m3 por hora.
b) 6m3 por hora.
c) 15m3 por hora.
d) 18m3 por hora.
3.
(UNEMAT) Se um cubo tem suas arestas aumentadas em 50%, o
seu volume aumentará em:
a) 237,5%
b) 337,5%
c) 50%
d) 235,5%
e) 100%
4.
(UNICAMP) Um cidadão precavido foi fazer uma retirada de
dinheiro em um banco. Para tanto, levou sua mala executiva, cujo
interior tem 56 cm de comprimento, 39 cm de largura e 10 cm de
altura. O cidadão só pretende carregar notas de R$ 50,00. Cada nota
tem 140 mm de comprimento, 65 mm de largura, 0,2 mm de espessura
e densidade igual a 0,75 g/cm3.
a) Qual é a máxima quantia, em reais, que o cidadão poderá
colocar na mala?
b) Se a mala vazia pesa 2,6 kg, qual será o peso da mala cheia de
dinheiro?
a) Encontre o valor de x, em centímetros, de modo que a
capacidade dessa caixa seja de 50 litros.
b) Se o material utilizado custa R$ 10,00 por metro quadrado,
qual é o custo de uma dessas caixas de 50 litros considerando-se
apenas o custo da folha retangular plana?
8.
(ITA) São dados dois cubos I e II de áreas totais S1 e S2 e de
diagonais d1 e d2, respectivamente. Sabendo-se que S1 – S2 = 54m2 e
que d2 = 3m, então o valor da razão
a) 3/2
9.
b) 5/2
d1
é:
d2
c) 2
d) 7/3
e) 3
(UNIFOR) Leia com atenção a tirinha em quadrinhos abaixo:
5.
(UERJ) As figuras a seguir mostram dois pacotes de café em pó
que têm a forma de paralelepípedos retângulos semelhantes.
Se o volume do pacote maior é o dobro do volume do menor, a
razão entre a medida da área total do maior pacote e a do menor é
igual a:
a) 3 3
b) 3 4
c) 6
d) 8
(DAVIS, Jim. Garfield um gato em apuros. Porto Alegre: L&PM,
2008,
p. 75 – Coleção L&PM Pocket)
Garfield passa seus melhor momentos na sua caixinha, ou seja,
dormindo. Para fazer uma caixinha parecida com a do Garlfield, usa-se
um papelão com a forma de um retângulo, conforme a figura abaixo,
onde os cantos são retirados e as abas são dobradas.
6.
(UFG) Em uma aula de geometria espacial foi construído um
paralelepípedo retangular utilizando-se como arestas canudos inteiros
de refrigerantes, sendo oito canudos de 12 cm e quatro canudos de 16
cm. Para garantir que o paralelepípedo ficasse “firme” deveriam ser
colocados suportes nas diagonais do paralelepípedo. Tendo em vista
esses dados, qual o comprimento da diagonal do paralelepípedo?
7.
(UNICAMP) A figura abaixo é a planificação de uma caixa sem
tampa:
Sabendo que o volume da caixa é de 384m3, que o comprimento é
três vezes a altura e, por sua vez, a altura é metade da largura, quantos
metros quadrados devem ser cortados nos quatro cantos do papelão
para fazer a caixinha do Garfield?
a) 16m2
b) 32 m2
c) 64 m2
d) 128m2 e) 256m2
10. (FUVEST) Dois blocos de alumínio, em forma de cubo, com
arestas medindo 10 cm e 6 cm, são levados juntos à fusão e, em
seguida, o alumínio líquido é moldado como um paralelepípedo reto
de arestas 8 cm, 8 cm e x cm. O valor de x é:
www.colegiopodium.com.br
RESPONSABILIDADE AMBIENTAL – Nossos papéis são de florestas 100% plantadas e renováveis
-1-
a) 16
b) 17
c) 18
d) 19
e) 20
11. (UFTM) Um paralelepípedo reto-retângulo de dimensões a, b e c,
cubos menores dos centros de cada face e um cubo menor do seu
centro. A figura I mostra o que restou do cubo maior, enquanto a
figura II mostra o que foi retirado do cubo.
dadas em centímetros, cujo volume é 1080 cm3, tem duas faces
paralelas e congruentes, de dimensões a e b, cujas áreas somam 216
cm2 e representam as suas bases.
Sabendo-se que a e b são números inteiros, tais que o
mmc  a,b   36 , e que a medida a é 3 cm maior que a medida b, podese concluir que a soma das áreas de todas as faces desse paralelepípedo
é, em cm2, igual a
a) 696.
b) 636.
c) 616.
d) 576.
e) 432.
12. (UFMA) Seja um paralelepípedo retângulo de dimensões p, q, r.
a) Calcule o volume da figura I.
b) Calcule a área da superfície da figura II.
17. (UNCISAL) Se a diagonal de uma face de um cubo mede 6 2 ,
então a medida da diagonal desse cubo é
a) 6 3
b) 6 6
c) 8 2
d) 8 3
e) 12 3
Sabendo-se que a sua área total é igual a 78 m2 e o seu volume 39 m3,
1 1 1
então o valor de:   é:
p q r
a) 1 m–1
b) 2 m–1
c) 3 m–1
d) 4 m–1
e) 5 m–1
18. (UnB) As dimensões de um paralelepípedo retângulo são
13. (PUC) Um cubo tem área total igual a 72m2. Sua diagonal mede:
19. (Mackenzie) A figura representa a maquete de uma escada que
a) 2 6 m
b) 6m
c)
6m
d) 2 3m
e) 4 6 m
14. (OBMEP) Emília quer encher uma caixa com cubos de madeira
diretamente proporcionais aos números 2, 3 e 5. Se a diagonal desse
paralelepípedo mede 2 19 , indicando por V o seu volume, obtenha
V
.
2
foi construída com a retirada de um paralelepípedo reto-retângulo, de
outro paralelepípedo reto-retângulo de dimensões 12, 4 e 6. O menor
volume possível para essa maquete é
de 5 cm de aresta. Como mostra a figura, a caixa tem a forma de um
bloco retangular, e
alguns cubos já foram colocados na caixa.
A) Quantos cubos Emília já colocou na caixa?
B) Calcule o comprimento, a largura e a altura da caixa.
C) Quantos cubos ainda faltam para Emília encher a caixa
completamente, se ela continuar a empilhá-los conforme indicado na
figura?
a) 190
b) 180
c) 200
d) 194
e) 240
20. (FGV) A soma das medidas das 12 arestas de um paralelepípedo
reto-retângulo é igual a 140 cm.
Se a distância máxima entre dois vértices do paralelepípedo é 21
cm, sua área total, em cm2, é
a) 776.
b) 784.
c) 798.
d) 800.
e) 812.
21. (UNICAMP) Um queijo tem o formato de paralelepípedo, com
15. (OBMEP) Um bloco retangular de madeira tem 320cm de
dimensões 20 cm × 8 cm × 5 cm. Sem descascar o queijo, uma pessoa
o divide em cubos com 1 cm de aresta, de modo que alguns cubos
ficam totalmente sem casca, outros permanecem com casca em apenas
uma face, alguns com casca em duas faces e os restantes com casca em
três faces. Nesse caso, o número de cubos que possuem casca em
apenas uma face é igual a
comprimento, 60cm de largura e 75cm de altura. O bloco é cortado
várias vezes, com cortes paralelos às suas faces, de modo a subdividilo em blocos também retangulares de 80cm de comprimento por
30cmde largura por 15cm de altura.
a) 360.
b) 344.
c) 324.
d) 368.
22. Considere o paralelepípedo reto-retângulo maciço da figura.
A
2c
m
B
a) Quantas peças foram obtidas?
b) Um metro cúbico dessa madeira pesa aproximadamente 900
quilogramas. Qual é o peso de cada uma dessas peças?
3c
m
4c
m
Se uma formiguinha sai de A e vai até B pelo caminho mais curto,
que distância ela deverá caminhar?
16. (UEG) Considere um cubo com 3 cm de aresta, subdividido em
cubos menores, cada um com 1 cm de aresta. Dele foram retirados
Goiânia-GO - Fone: 3088-0088 – www.colegiopodium.com.br
-2-
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
Gabarito
D
D
A
a) R$600.000,00
b) 18,98kg
B
d  544 cm
a) x = 50 cm.
b) R$8,40.
C
C
D
B
A
B
a) 31 cubos
b) 50 cm, 35 cm e 30 cm
a) 40 peças
b) 32,4 kg
a) 20 cm3
b) 30 cm2
A
60
E
B
A
41 cm
b) a área de uma face lateral;
c) 389 cubos
c) a área lateral;
d) a área total;
e) o volume;
2.
(ITA) Dado um prisma hexagonal regular, sabe-se que sua altura
mede 3 cm e que sua área lateral é o dobro da área de sua base. O
volume desse prisma, em cm3, é:
a) 27 3
Prisma
Considere um prima de área da base AB e altura H, onde a altura
do prisma é a distância entre os planos das bases.
c) 12
b) 13 2
d) 54 3
e) 17 5
3.
(UnB) Em um prisma triangular regular, a área lateral é o
quádruplo da área da base. Sabendo que o triângulo da base pode ser
inscrito em uma circunferência de raio 2 dm, calcule a área total do
prisma em dm2 e multiplique o resultado por 3 .
4.
(UFG) O projeto Icedream é uma iniciativa que tem como meta
levar um iceberg das regiões geladas para abastecer a sede de países
áridos. A ideia do projeto é amarrar a um iceberg tabular uma cinta e
rebocá-lo com um navio. A figura a seguir representa a forma que o
iceberg tem no momento em que é amarrada à cinta para rebocá-lo.
Prisma Reto
Classificação de um prisma
a) Prisma reto: é qualquer prisma cujas arestas laterais são
perpendiculares ao plano da base.
b) Prisma oblíquo: é qualquer prisma cujas arestas laterais são
oblíquas ao plano da base.
c) Prisma regular: é qualquer prisma reto cujas bases são
polígonos regulares.
 Área da base de um prisma (AB): Área delimitada pelo
polígono da base.
 Área lateral de um prisma (AL): Soma das áreas das faces
laterais.
 Área total de um prisma (AT): Soma das áreas de todas as faces
do prisma, ou seja, AT  AL  2.AB.
 Volume: V  AB  H .
1.
Considerando que o iceberg é formado somente por água potável
e que, após o deslocamento, 10% do volume do bloco foi perdido,
determine qual a quantidade de água obtida transportando-se um
iceberg com as dimensões, em metros, indicadas na figura apresentada.
EXERCÍCIOS PROPOSTOS
(PUC) Tem-se um prisma de base hexagonal, cuja altura é
h  3 e cujo raio do círculo que circunscreve a base é R  2. A área
total deste prisma é:
1.
EXERCÍCIOS EM SALA
Considere o prisma regular de base hexagonal da figura.
a)
3
b) 24 3
c) 30
d) 10 2
e) 8
2.
(VUNESP) As faces de um paralelepípedo retangular têm áreas 6
cm2, 9 cm2 e 24 cm2. O volume desse paralelepípedo é
a) 1.296cm 3
b) 48cm 3
c) 39cm 3
d) 36cm 3
Desse prisma, calcule:
a) a área da base e o apótema da base;
3.
e) 6 6 cm 3
(PUC) A figura abaixo mostra a seção transversal de uma piscina
com 20m de comprimento por 15m de largura, cuja profundidade varia
uniformemente de 1m a 3m.
Goiânia-GO - Fone: 3088-0088 – www.colegiopodium.com.br
-3-
Considerando-se que o volume dessa piscina é o produto da área
da seção exibida pela largura da piscina, é CORRETO afirmar que a
capacidade máxima da mesma, em litros, é igual a:
a) 600
b) 6.000
c) 60.000
d) 600.000
Considerando 3  1,73 , é correto afirmar que a capacidade
desse recipiente é, em mL, aproximadamente,
a) 934.
b) 1 150. c) 650.
d) 865.
e) 1 350.
4.
11. (FGV) Uma piscina tem o formato de um prisma hexagonal
(UFG) Uma piscina, com o formato de um prisma, possui as
dimensões que estão ilustradas na figura abaixo:
3
m.
2
Cada lado do hexágono mede 2 m. O volume de água necessário
para encher 80% do volume da piscina é igual a:
a) 6,9 m3 b) 7 m3
c) 7,1 m3 d) 7,2 m3 e) 7,3 m3
regular reto com profundidade igual a
12. (FGV) A figura mostra a maquete do depósito a ser construído. A
escala é 1 : 500, ou seja, 1cm, na representação, corresponde a 500 cm
na realidade.
Qual será a capacidade, em metros cúbicos, do depósito?
Calcule o volume de água contida na piscina, quando ela está com
água até os seus 3 metros de altura.
5.
(VUNESP) Uma piscina de forma retangular tem 8 m de largura,
15 m de comprimento, 0,9 m de profundidade num de seus extremos e
2,7 m de profundidade no outro extremo, sendo o seu fundo um plano
inclinado. Calcule o volume de água da piscina quando a altura do
nível da água é de 0,6 m na extremidade mais funda.
6.
(Unesp) Considere um prisma hexagonal regular, sendo a altura
igual a 5 cm e a área lateral igual a 60 cm2.
a) Encontre o comprimento de cada um de seus lados.
b) Calcule o volume do prisma.
7.
1.
2.
3.
4.
5.
Gabarito – Exercícios Propostos
B
D
D
825m3 de água
12 m 3 ou 12.000 litros.
8.
6.
7.
8.
9.
10.
11.
12.
a) 2cm
b) 30 3 cm3
D
a) 8 dm, b) 512 .
a) V = 1980 cm3
b) V0 = 1650 cm3
A
D
3240 m3
(ITA) Dado um prisma hexagonal regular, sabe-se que sua altura
mede 3 cm e que sua área lateral é o dobro da área de sua base. O
volume deste prisma, em cm3, é:
a) 27 3
b) 13 2
c) 12
d) 54 3
e) 17 5
(UNICAMP) Ao serem retirados 128 litros de água de uma caixa
d’água de forma cúbica, o nível da água baixa 20 cm.
a) Calcule o comprimento das arestas da referida caixa.
b) Calcule a sua capacidade em litros (1  equivale a 1 dm3).
9.
(UFJF) Uma empresa de sorvete utiliza como embalagem um
prisma reto, cuja altura mede 10 cm e cuja base é dada conforme
descrição a seguir: de um retângulo de dimensões 20 cm por 10 cm,
extrai-se em cada um dos quatro vértices um triângulo retângulo
isósceles de catetos de medida 1cm.
a) Calcule o volume da embalagem.
b) Sabendo que o volume ocupado por esse sorvete aumenta em
1
(um quinto) quando passa do estado líquido para o estado sólido,
5
qual deve ser o volume máximo ocupado por esse sorvete no estado
líquido, nessa embalagem, para que, ao congelar, o sorvete não
transborde?
10. (UFTM) Um rótulo de forma retangular (figura 1) será colado em
toda a superfície lateral de um recipiente com a forma de um prisma
hexagonal regular (figura 2), sem haver superposição.
Goiânia-GO - Fone: 3088-0088 – www.colegiopodium.com.br
-4-