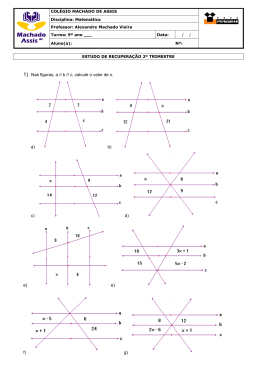
 PARTE A 
1) Dada a figura, calcule os elementos pedidos, para cada uma das hipóteses a seguir:
x
y
z
a) Se y  3cm e z  4cm , calcule x .
b) Se y  6cm e z  8cm , calcule x .
c) Se y  1,5cm e z  2cm , calcule x .
d) Se x  13cm e z  12cm , calcule y .
e) Se x  20cm e z  12cm , calcule y .
f) Se x  100cm e y  60cm , calcule z .
g) Se x  17cm e y  8cm , calcule z .
2) Para o triângulos retângulo em cada item determine o que é pedido.
a) Os catetos medem, respectivamente, 30cm e 40cm; determine a medida da hipotenusa.
b) Os catetos medem, respectivamente, 5cm e 12cm; determine a medida da hipotenusa.
c) Um cateto mede 15cm e a hipotenusa mede 17cm; determine a medida do outro cateto.
d) Um cateto mede 10cm e a hipotenusa mede 26cm; determine a medida do outro cateto.
3) Em uma indústria as caixas armazenadas no subsolo são transportadas para o andar térreo com a ajuda
de uma esteira de 7,5m de comprimento. O esquema “subsolo-esteira-térreo” descrito está representado
na figura a seguir. Determine a medida H do “pé-direito” (ou “altura”) do subsolo sabendo que a caixa ao
ser transportada tem um deslocamento horizontal, “d”, igual a 4,5m.
Térreo
ira
te
Es
H
Caixa
Subsolo
d
1
4) Determine o perímetro e a área do trapézio retângulo.
5 cm
10
c
m
13 cm
5) Calcule o perímetro do triângulo, a seguir, sabendo que sua área mede 60cm2.
15 cm
6) Uma escada de 3,0 m de comprimento está apoiada em uma parede e seu pé dista 1,8 m da parede.
Determine a altura que a escada atinge a parede.
 PARTE B 
7) De acordo com cada figura, determine o valor das incógnitas indicadas.
a)
b)
x+
13cm
c)
12cm
y
5
x+2
9
x+
6
5
3cm
x+5
x
8) Desenhe um retângulo de lados 12cm e 5cm e em seguida determine a medida de suas diagonais.
9) Dois amigos, João e Maria, estão de mãos dadas no centro de uma quadra poliesportiva e decidem se
separar caminhando em direções perpendiculares. Então, João dá 15 passos e Maria dá 8 passos.
Considerando que cada passo deles mede 0,5m, qual a distância que agora os separa?
2
10) Em um triângulo isósceles a altura mede 8cm e a base relativa mede 12cm. Determine as medidas dos
lados congruentes.
 PARTE C 
11) Dois ciclistas partem de uma mesma cidade em direção reta; um em direção leste e outro em direção
norte, suas velocidades são de 30 km/h e 40 km/h respectivamente. Após duas horas os ciclistas param.
a) Desenhe a situação descrita.
b) Determine a distância que separa os dois ciclistas após as duas horas.
12) Calcule a área de um triângulo isósceles de lados medindo 8cm, 5cm e 5 cm.
13) Determine o valor da incógnita de acordo com as figuras.
b)
8
A
17
B
A
15
x -1
3
x
x+
9
x+
a)
15
B
14) Quantos metros tem o perímetro de um losango cujas diagonais medem 14cm e 48cm,
respectivamente?
15) Uma antena de 18m de altura, usada para transmissões de rádio, após um vendaval dobra-se em um
ponto de tal maneira que o topo da antena toca o chão plano em um ponto que dista 6 metros de sua base.
A outra parte da antena continua perpendicular ao chão. A que altura encontra-se o ponto onde foi
dobrada a antena?
 PARTE D 
16) Calcule a hipotenusa de um triângulo retângulo em que um dos catetos mede 5m e a altura relativa à
hipotenusa mede 3m.
3
17) O menor dos lados de um trapézio retângulo é a base menor. Calcule o perímetro do trapézio sabendo
que os lados desse quadrilátero são números inteiros consecutivos.
18) Os raios de dois círculos medem 15m e 20m e a distância de seus centros tem 25m. Calcule o
comprimento da corda comum.
 RESPOSTAS 
1)
a) x  5cm
b) x  10cm
c) x  2,5cm
e) y  16cm
f) z  80cm
g) z  15cm
2) a) Hipotenusa: 50cm
b) Hipotenusa: 13cm
d) y  5cm
c) Cateto: 8cm
d) Cateto: 24cm
3) 6m é a medida do “pé direito”.
4) Perímetro: 34cm; Área: 54cm2
5) Perímetro: 40cm
6) Altura de 2,4m.
7) a) x  4cm e y  5cm
b) x  10
c) x  7
8) As diagonais medem 13cm.
9) A distância que os separa é de 8,5m.
10) Os lados congruentes medem 10cm cada.
11) a) Desenho
b) 100km.
12) 12cm2
13) a) x  5
b) x  7
14) O perímetro tem 1m.
15) O ponto encontra-se a 8m de altura.
16) A hipotenusa mede
25
m (ou 6,25 m).
4
17) O perímetro é 18.
18) A corda mede 24m.
4