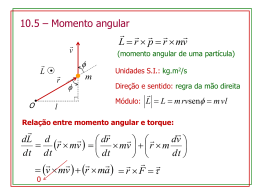
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.

Introdução:
Ao usarmos uma chave de roda para retirar o
parafuso para trocar o pneu de um automóvel, a roda
inteira pode começar a girar, a menos que você descubra
um meio de mantê-la firme. O que ocorre com a força
que você realiza sobre a chave de roda que ocasiona a
rotação da roda? De modo geral, o que produz a
aceleração angular em um corpo que gira? Uma força
pode puxar, empurrar mas para produzir um movimento
de rotação é necessária uma ação giratória ou de
rotação.
Analisaremos uma nova grandeza física, o
torque, que descreve a ação giratória da força.
Desenvolveremos um novo princípio de
conservação, a lei da conservação do momento angular,
que é extremamente útil para entender o movimento de
rotação do corpo rígido e de corpos não rígidos. Uma
aplicação interessante é o movimento de um giroscópio,
que se comporta de acordo com a dinâmica do
movimento de rotação.
1
Torque
Definimos como torque, ou momento da força
F em relação a um ponto O como sendo o produto da
distância l perpendicular entre o ponto O e a linha de
ação da força e o módulo da força
  F l
Em notação vetorial:
  r F
 Unidade: N.m
F : F . Assim:
 Exemplo 1 – Um bombeiro hidráulico, incapaz
de afrouxar a conexão de um tubo, encaixa um pedaço
de sucata (―uma alavanca‖) sobre a haste da chave de
grifa. A seguir ele usa seu peso de 900 N para ficar em
pé na extremidade da alavanca. A distância entre o
centro da conexão e o ponto onde o peso atua é igual a
0.80 m, e o eixo da alavanca faz um ângulo de 19° com
a horizontal.
Calcule o módulo, a direção e o sentido do
torque que ele aplica em torno do centro de conexão.
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.

Solução:
O ângulo  entre r e F é igual a 190°. Assim,
o braço l da alavanca é:
l  0.8 sen109  l  0.76m
  F  l   900 0.76
  680N  m
 Torque e aceleração angular de um corpo
rígido.
2
A relação fundamental para a dinâmica da
rotação de um corpo rígido pode ser feita se
imaginarmos que o corpo constituí de um número
grande de partículas. Escolhemos para o eixo de rotação
o eixo Oy; a primeira partícula de massa m1 está a uma
distância r1 do eixo. Assim, a segunda lei de Newton
para o movimento tangencial é:
 Exemplo 2 – Desenrolando um cabo. A
figura mostra a mesma situação mostrada no exemplo
do capítulo anterior.
F1,tan  m1  a1,tan
F1,tan  r1  m1  r12  
Somando sobre todas as partículas:
    m  r   
2
i
i
i
Segunda lei de Newton para o movimento de
rotação:
  I 
Um cabo é enrolado diversas vezes em torno de
um cilindro sólido uniforme que pode girar em torno de
seu eixo. O cilindro possui diâmetro igual a 0.120 m e
massa de 50 kg. O cabo é puxado com uma força de 9.0
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
N. Supondo que o cabo seja desenrolado sem se dilatar
e sem deslizar, qual sua aceleração?

Solução:
  F  l   9 0.060
  0.54N  m
1
I  M  R2
2
1
I  50  0.062
2
I  0.09  kg  m2 


I
0.054
rad

   6.0 2
0.090
s
 Exemplo 3 – Desenrolando um cabo II.
Suponha a mesma situação mostrada no exemplo
anterior. Ache a aceleração do objeto de massa m e a
aceleração angular do cilindro.
a  atan  R 
1
m g  M  a  m a
2
g
a
M
1
2m
1
T  M a
2
1
g
T  M
M
2
1
2m
M
g
M 2m  g
T

T 

2 2m  M
2 2m  M
2m
m M
T
g
2m  M
 Exemplo 4 – Um cavaleiro de massa m1
desliza sem atrito ao longo de um trilho de ar horizontal.
Ele está ligado a um objeto de massa m2 por meio de um
fio de massa desprezível. A polia é uma casca cilíndrica
(ligada ao centro por raios de massa desprezível) com
massa M e raio R, e o fio faz o cilindro sem deslizar
nem dilatar. Ache a aceleração angular da polia e a
tensão em cada parte do fio.
 Solução:
As equações de movimento para o cavaleiro e o
objeto são:
 Solução:
F
y
F
 m g T  m a
O peso Mg e a força normal N não possuem
torque em relação ao eixo de rotação.
Assim:
  I 
R  T  I   R  T 
1
M  R2 
2
a
R
T
1
M a
2
F
y
x
 T1  m1  a1
 m2  g  T2  m2  a2
Momento de inércia da polia em torno do eixo:
I  M  R2
Considerando positivo o sentido da rotação dos
ponteiros do relógio, a equação do movimento da polia
é:
  I   T  R  T  R  M  R
2
1
2

Como o fio não dilata nem desliza, temos as
relações cinemáticas adicionais:
3
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
a1  a2  R 
Juntando as equações, teremos:
T1  m1  a1


m2  g  T2  m2  a2
 T T  M a
1
 2 1
Somando
eliminando-se T1 e T2:
a1 
as
três
equações
e
m2
g
m1  m2  M
4
Substituindo na relação acima:
m1  m2
g
m1  m2  M
 m  M   m2  g
T2  1
m1  m2  M
T1 
 Movimento combinado de rotação
translação: Relações envolvendo energia.
e
Todo movimento de um corpo rígido pode ser
sempre dividido em um movimento de translação do
centro de massa e outro de rotação em torno do centro
de massa. A energia cinética do corpo possui duas
parcelas: uma devida à translação do centro de massa e
outra devida à rotação:
1
1
2
K  M  vcm
 Icm  2
2
2

Condição para rolamento sem deslizamento:
vCM  R 
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
 Exemplo 5 – Enrolamento de uma casca
cilíndrica. Uma casca cilíndrica oca de raio R e massa
M rola sem deslizar com uma velocidade vCM ao longo
de uma superfície plana. Qual a sua energia cinética?

Solução:
 Exemplo 7 – Competição entre corpos
girando. Em uma demosntração durante a aula de
física, o professor faz uma ―competição‖ de vários
corpos rígidos redondos, deixando-os rolar do alto de
um plano inclinado. Qual a forma do corpo que alcança
primeiro a parte inferior?
1
1
2
K  M  vcm
 Icm  2
2
2
2
1
1
 vCM 
2
2
K  M  vcm   M  R   

2
2
 R 
2
K  M  vcm
 Exemplo 6 – Velocidade de um ioiô. Um ioiô
é feito enrolando-se um fio diversas vezes em torno de
um cilindro de massa M e raio R. Mantém-se presa a
extremidade enquanto o cilindro é liberado sem
velocidade inicial. O fio se desenrola, mas não desliza
nem se dilata à medida que o cilindro cai e gira. Use
considerações de energia para achar a velocidade do
centro de massa vCM do cilindro sólido depois que ele
caiu a uma distância h.
5
 Solução:
K1  0 U1  M  g  h U2  0
1
1
2
K2  M  vcm
 Icm   2
2
2
K1 U1  K2 U2
1
1
2
0  M  g  h  M  vcm
 Icm  2  0
2
2
Chamando de:
I cm  c  M  R 2
2
 Solução:
1
1
2
K  M  vcm
 Icm  2
2
2
v
1
  CM  I  M  R2
R
2
2
1
1 1
2
2  vCM 
K2  M  vcm   M  R  

2
2 2
 R 
3
2
K2  M  vcm
4
Aplicando a conservação da energia:
K1 U1  K2 U2
3
2
0  M  g  h  M  vcm
0
4
vcm 
4
g h
3
1
1
v 
2
M  g  h  M  vcm
 c  M  R2   cm 
2
2
 R 
1
1
2
2
M  g  h  M  vcm
 M  vcm
c
2
2
1
2 gh
2
M  g  h  M  vcm
1  c   vcm 
2
1 c
Todos os cilindros sólidos possuem a mesma
velocidade no ponto inferior do plano, mesmo quando
possuem massas e raios diferentes, pois eles possuem o
mesmo valor da constante c. Todas as esferas sólidas
possuem a mesma velocidade na base do plano. Quando
menor o valor de c maior a velocidade do corpo quando
ele chega na parte inferior do plano. Observando a
tabela de momento de inércia, vemos que a ordem de
chegada do plano é: Qualquer esfera maciça, qualquer
cilindro maciço, qualquer esfera oca com parede fina ou
casca esférica e, finalmente, qualquer casca cilíndrica.
 Exemplo 8 – Aceleração de um ioiô. Ache a
aceleração de cima para baixo do ioiô e a tensão no fio.
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
2
T  M g
3
 Exemplo 9 – Aceleração de uma esfera
rolando. Uma esfera de bliche sólida rola sem deslizar
para baixo de uma rampa ao longo de uma guia. O
ângulo de inclinação da rampa em relação à horizontal é
. Qual é a aceleração da bola? Considere a bola uma
esfera homogênea sólida, desprezando seus orifícios.
6
 Solução:
A equação para o movimento de translação do
centro de massa é:
F
y
 M  g  T  M  acm
O momento de inércia em relação a um eixo
que passa pelo centro de massa:
1
I  M  R2
2
Somente a força de tensão possui torque em
relação a um eixo que passa pelo centro de massa é:
1
  T  R  Icm   T  R  2 M  R2 
Como o fio se desenrola sem se deslizar:
vCM  R 
aCM  R    
T
aCM
R
1
M  R 
2
acm
1
T  M  acm
2
M  g T  M  acm
1
M  g  M  acm  M  acm
2
1
M  g  M  acm  M  acm
2
3
2
M  g  M  acm  acm  g
2
3
1
T  M  acm
2
1
2
T  M g
2
3
 Solução:
A figura mostra o diagrama de corpo livre,
mostrando o sentido positivo das coordenadas.
Usando o momento de inércia da esfera sólida:
2
I  M  R2
5
Equações de translação e rotação do centro de
massa e chamando de f a força de atrito:
F
x
 M  g  sen  f  M  acm
  f  R  I
Como:
2
   f  R  M  R2  
5
a
 R     CM
R
cm
aCM
Substituindo, teremos:
2
M  acm
5
M  g  sen  f  M  acm
2
M  g  sen  M  acm  M  acm
5
2
M  g  sen  M  acm  M  acm
5
7
5
M  g  sen  M  acm  acm   g  sen
5
7
2
2
5
f  M  acm  f  M   g  sen
5
5
7
2
f   M  g  sen
7
f 
Coeficiente de atrito:
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
2
 M  g  sen
f
7
 
N
M  g  cos 
2
  tg 
7
 Exemplo 10 – Um anúncio fazendo
propaganda da potência desenvolvida pelo motor de um
automóvel afirma que o motor desenvolve 1.49.10 5W
para uma rotação de 6000 rpm. Qual é o torque
desenvolvido pelo motor?

Solução:
dW  Ftan ds  ds  R  d
dW  Ftan R  d
dW    d
6000
f  6000rpm 
Hz
60
f  100Hz
 Trabalho e potência no movimento de rotação
Podemos escrever:
2
W     d
1
Podemos desenvolver:
dW    d
dW  I   d  dW  I 
d
 d
dt
dW  I   d
d
 d
dt
dW  I 
2
W   I    d
1
1
1
I  22  I  12
2
2
dW
d
 
dt
dt
P   
Wtot 
P      
P

rad
  2  f    2 100    200
s
5
1.49 10

200
  237N  m
 Exemplo 11 - Um motor elétrico desenvolve
um torque constante de  = 10 N.m sobre o esmeril
montado no seu eixo motor. O momento de inércia é I =
2.0 kg.m². Sabendo que o sistema começa a se mover a
partir do repouso, calcule o trabalho realizado pelo
motor em 8.0 s e a energia cinética no instante final.
Qual a potência média desenvolvida pelo motor?
 Solução:
  I    

I
10
rad
    2
2
s
   t
rad
  5  8    40
s
1
1
K  I  2  K  2  402  K  1600J
2
2
1
1
    t 2    5  82    160rad
2
2
W    W  10160 W  1600J
W
1600
P
P
 P  200W
t
8
A potência instantânea P = não é constante,
porque  cresce continuamente. Porém podemos
calcular o trabalho total por:
t2
t2
t1
t1
W   P  dt  W       dt
7
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
t2
8
W       t  dt   10  5  tdt
t1
0
W  50
2 t 8
t
2
 W  1600 J
t 0
 Momento angular
Uma grandeza análoga ao momento linear p de uma
partícula é o momento angular, que representamos por
L . Definimos como:
8
Lrp
Para um corpo rígido de i partículas, o momento
angular de cada uma será:
Li  mi  vi  ri
Li  mi   ri  i   ri
Li  mi  ri 2  i
L   Li  L   mi  ri2  i
L  I 
L  m  v  r  sen
L  m v  l
Pode-se mostrar que a taxa de variação do momento
angular é igual ao torque da força resultante:
dL dr
dp

 pr
dt dt
dt
dL dr
mdv

 mv  r 
dt dt
dt
dL
 v  mv  r  ma
dt
0
dL
 r F
dt
dL

dt
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
9
 Exemplo 12 – A hélice da turbina de um motor
a jato possui momento de inércia 2.5 kg.m² em torno do
eixo de rotação. Quando a turbina começa a girar, sua
velocidade angular em função do tempo é dada por
  400  t 2  rad s 3 
(a) Calcule o momento angular da hélice em função
do tempo e ache seu valor em t = 3.0 s.
(b) Determine o torque resultante que atua sobre a
hélice em função do tempo e calcule seu valor para t =
3.0 s.
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
 Solução:
2
(a) L  I    L  2.5  400  t
L  1000  t 2
kg  m2
L  t  3  1000  32  L  9000
s
dL
(b)  
   1000  2t
dt
  2000  t
 t  3  2000  3    6000N  m

Conservação do momento angular
Princípio da conservação do momento angular: Esse
princípio vale em todas escalas, desde o sistema
atômico como o planetário e decorre da equação:
dL

dt
dL
0
Quando  i  0 
dt
i
Podemos escrever também:
I1  1  I 2  2
 Exemplo 13 – Qualquer um pode ser
bailarino. Um professor de física acrobata está de pé
sobre o centro de uma mesa girante, mantendo seus
braços estendidos horizontalmente com um haltere de
5.0 kg em cada mão.
Ele está girando em torno de um eixo vertical
completando uma volta a cada 2.0 s. Calcule a nova
velocidade angular do professor quando ele aproxima os
dois halteres do seu estômago e discuta como isso
modifica a sua energia cinética. Seu momento de
inércia (sem os halteres) é igual a 3.0 kg.m² quando seus
braços estão distendidos para fora, diminuindo para 2.2
kg.m² quando suas mãos estão próximas do seu
estômago. Os halteres estão inicialmente a uma
distância de 1.0 m do eixo e a distância final é igual a
0.20 m. Considere o halteres como partículas.

Solução
I  I prof  I halteres
I1  3  2  5 12
I1  13kg  m2
I 2  2.2  2  5  0.22
I 2  2.6kg  m2
f 
1
1
rad
 f  Hz    2 f    
T
2
s
I1  1  I 2  2
I1
13
rad
 1  2 
   2  5
I2
2.6
s
I
13
f2  1  f1  f2 
 0.5  f2  2.5Hz
I2
2.6
1
1
K1  I1  12  K1  13  2  K1  64J
2
2
1
1
2
K2  I2  22  K2  2.6  5   K1  320J
2
2
2 
 Exemplo 14 – A figura mostra 2 discos, um
deles é o volante de um motor e o outro é um disco
ligado a um eixo de transmissão. Seus momentos de
inércia são IA e IB, respectivamente; inicialmente eles
estão girando com a mesma velocidade angular A e B,
respectivamente. A seguir empurramos os dois discos
um contra o outro aplicando forças que atuam ao longo
do eixo, de modo que sobre nenhum dos dois discos
surge torque em relação ao eixo. Os discos permanecem
unidos um contra o outro e atingem uma velocidade
angular final . Deduza uma expressão para .
10
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
 Solução:
O único torque que atua sobre cada disco é o torque
que cada disco exerce sobre o outro disco; não existe
nenhum torque externo. Logo o momento angular total
do sistema dos dois discos é o mesmo antes e depois de
eles serem unidos. No equilíbrio final eles giram juntos
como se constituíssem um único corpo com momento
de inércia:
I  IA  IB
A conservação do momento angular fornece:
I A A  IB B  I 
I   I 
 A A B B
I
I A  A  I B  B

I A  IB
completamente inelástica. Não deveríamos esperar
conservação da energia cinética, embora a força externa
resultante e o torque resultante sejam nulos, porque
existem forças internas não conservativas (forças de
atrito) que atuam enquanti os dois discos começam a
girar unidos e tendem a girar com uma velocidade
angular comum.
 Exemplo 16 – Momento angular em uma
ação policial. Uma porta de largura 1 m e massa de 15
kg é articulada com dobradiças em um dos lados de
modo que possa girar sem atrito em torno de um eixo
vertical. Ela inicialmente não está aberta. Um policial dá
um tiro com uma bala de 10 g e velocidade de 400 m/s
exatamente no canto da porta. Calcule a velocidade
angular da porta imediatamente depois que a bala
penetra na porta. A energia cinética se conserva?
 Exemplo 15 – No exemplo anterior, suponha
que o volante A tenha massa de 2.0 kg, um raio de 0.20
m e uma velocidade angular inicial de 200 rad/s.
Calcule a velocidade angular comum final  depois que
os discos ficam em contato. A energia cinética se
conserva nesse processo?
 Solução:
1
1
I A  mA  rA2  I A  2  0.22  I A  0.040kg  m2
2
2
1
1
2
I B  mB  rB  I B  4  0.12  I B  0.020kg  m2
2
2

I A  A  I B  B
I A  IB
0.04  50  0.02  200
0.04  0.02
rad
  100
s
1
1
K1  I A  A2  I B  B2
2
2
1
1
K1  0.04  502  0.02  2002
2
2
K1  450J
1
K2   I A  I B    2
2
1
K2   0.04  0.02 1002
2
K2  300J

Um terço da energia foi perdida na ―colisão
angular‖, o análogo rotacional de uma colisão linear
 Solução:
Considere um sistema formado pela porta
juntamente com a bala em seu interior. Não existe
nenhum torque externo em torno do eixo definido pelas
dobradiças, de modo que o momento angular em torno
desse eixo deve se conservar. O momento angular da
bala é:
L  m v  l  L  0.01 400  0.5
L  2kg  m 2 s
O momento angular final é:
L  I 
I  I porta  I bala
I
mp  d 2
 mbala  l 2
3
15 12
I
 0.010  0.52
3
I  5.0025kg  m2
m v  L
L  I    
I
2
rad

   0.40
5.0025
s
11
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
A colisão entre a porta e a bala é inelástica porque
forças não conservativas atuam durante o impacto da
bala. Logo, não esperamos que haja conservação da
energia cinética. Para conferirmos, calculamos a energia
cinética inicial e final:
1
1
K1  m  v2  K1  0.010  4002
2
2
K1  800 J
1
K2  I   2
2
1
K2  5.0025  0.42
2
K2  0.40J
A energia cinética final é apenas 1/2000 da energia
cinética inicial.
Giroscópios e precessão
Se o eixo do volante for inicialmente colocado
horizontalmente e depois largado, sua extremidade livre
começará a cair sob a ação da gravidade, se o volante
inicialmente não estava girando. Porém, quando o
volante está inicialmente girando, o que ocorre é
basicamente diferente. Um movimento possível é o
movimento circular uniforme do eixo em um plano
horizontal combinado com o movimento de rotação do
volante em torno desse eixo. Esse movimento
surpreendente, que não é intuitivo, denomina-se
precessão. A precessão ocorre na natureza, assim como
nas máquinas que giram, como no caso do giroscópio. A
Terra sofre precessão: seu eixo de rotação ( o eixo que
liga o pólo norte ao pólo sul) muda constantemente de
direção, e a direção desse eixo só retorna exatamente à
posição inicial depois de um ciclo completo de
precessão que dura 26000 anos.
Para estudar o estranho fenômeno da precessão,
devemos nos lembrar que o torque, o momento angular
e o linear são grandezas vetoriais. Em particular,
precisamos da relação geral entre o torque resultante
 que atua sobre um corpo e a taxa de variação de
momento angular L , dada por
dL
  dt .
Vamos
inicialmente aplicar essa equação ao caso em que o
volante não está girando. Tomamos a origem sobre o
ponto O do pivô e supomos que o volante seja
simétrico, com massa M e momento de inércia I em
torno do eixo do volante. O eixo do volante está
inicialmente na direção ao longo do eixo Ox. As únicas
forças que atuam sobre o giroscópio são a força normal
que atua sobre o pivô N e o peso w do volante que atua
no centro de massa, situado a uma distância r do pivô.
A força normal possui torque nulo em relação ao
pivô e o peso possui torque  na direção do eixo Oy ,
como indicado na figura a seguir.
Inicialmente não existe rotação e o momento angular
inicial Li
 0 .Pela equação:
dL
  dt
A variação dL do momento angular em um intervalo de
tempo curto dt é:
dL    dt
12
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
Essa variação está na direção Oy porque  também
está. À medida que decorre cada intervalo de tempo dt, o
momento angular varia em incrementos adicionais dL
na direção Oy porque a direção do torque é constante. O
aumento crescente do momento angular horizontal
significa que o giroscópio gira para baixo com
velocidade crescente em torno do eixo Oy até que ele
atinja o suporte ou então que caia na mesa onde ele se
apoia.
Vamos agora analisar o que ocorre quando o
volante está inicialmente girando, de modo que o
momento angular inicial
Li não é igual a. Uma vez que
o volante gira em torno do eixo de simetria Li está ao
longo desse eixo. Porém, cada variação de momento
angular
dL é perpendicular ao eixo, porque o torque
  r 
No instante indicado na Figura (a), o giroscópio
L . Depois de um intervalo de
tempo curto dt, o momento angular passa para L  dL
possui momento angular
a variação infinitesimal do momento angular e
dL    dt que é perpendicular a L . Como indica o
diagrama vetorial da Figura, isso significa que o eixo
do volante do giroscópio girou de um ângulo pequeno
d dado por:
é perpendicular ao eixo. Isso faz com que a
direção do eixo varie, porém seu módulo não varia. As
variações de dL ocorrem sempre no plano xy
horizontal, de modo que o vetor momento angular e o
eixo do volante que com ele se move estão sempre em
um plano horizontal. Em outras palavras, o eixo não cai
— ele apenas sofre precessão.
Caso isso ainda lhe pareça difícil, pense em uma
bola presa a um fio. Se a bola estiver inicialmente em
repouso e você puxar o fio para você, a bola também se
deslocará para você. Porém, se a bola estiver
inicialmente
se
movendo
e
você
puxá-la
perpendicularmente à direção do seu movimento, ela se
moverá em um círculo em torno de sua mão: ela não se
aproximará de sua mão. No primeiro caso a bola possuía
momento angular zero; quando você aplica uma força
F orientada para você durante um intervalo de tempo
dt, a bola adquire um momento linear dp  Fdt que
também está orientado para você. Porém, quando a bola
já possui um momento linear p , uma variação do
momento angular dp perpendicular a p produzirá uma
variação da direção do movimento, e não uma variação
do módulo da sua velocidade. Troque
p por L e F
por  neste raciocínio, e você verá que a precessão é
simplesmente o análogo relacional do movimento
circular uniforme.
d 
dL
L
A taxa com a qual o eixo se move. d/dt, denominase velocidade angular de precessão escalar:
representando essa grandeza por , achamos:
dL

L
d
 w r

 
dt
dt
L I 
Portanto a velocidade angular de precessão é
inversamente proporcional à velocidade angular da
rotação em torno do eixo. Um giroscópio que gira
rapidamente realiza uma precessão lenta; caso o atrito
nos mancais faça diminuir a velocidade angular do
volante, a velocidade angular de precessão aumenta. A
velocidade angular de precessão da Terra é muito lenta (
l rev/26000 anos) porque sua velocidade angular em
torno do eixo, ou velocidade angular de spin é muito
grande, e o torque 
devido às influencias
gravitacionais do Sol e da Lua é relativamente pequeno.
A medida que o giroscópio realiza uma precessão,
seu centro de massa se move em um círculo de raio r
sobre um plano horizontal. Seu componente vertical da
aceleração é zero, de modo que a torça normal de baixo
para cima N exercida pelo pivô deve ter módulo pre
cisamente igual ao peso. O movimento circular do
centro de massa com velocidade angular  necessita de
F orientada para o interior do círculo, com
2
módulo F  M   r . Essa força também deve ser
uma força
fornecida pelo pivô.
Uma hipótese básica que lidemos em nossa
analise do giroscópio foi que o vetor momento angular
L está associado somente com o momento angular de
13
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
spin do volante e e puramente horizontal. Contudo,
existirá também um componente vertical do momento
angular associado com o movimento de precessão do
giroscópio.
Ignorando isso estamos tacitamente
supondo que a precessão é lenta, isto é, que a velocidade
angular de precessão  é muito menor do que a
velocidade angular de spin . Como a Equação anterior
de  mostra, um valor elevado de  automaticamente
fornece um valor pequeno de , de modo que essa
aproximação é razoável. Quando a precessão não é
lenta, efeitos adicionais mostram que surge um
movimento ondulado de cima para baixo, denominado
nutação do eixo do volante, que se superpõe com o
movimento de precessão. Você pode ver o movimento
de nutação ocorrendo em um giroscópio à medida que
sua velocidade angular de spin diminui, de modo que 
aumenta, e o componente vertical de
mais desprezado.
Dessa maneira, o giroscópio serve como referência de
direção, mas não de posição. Ou seja, é possível movimentar um
giroscópio normalmente no espaço sem qualquer trabalho além do
necessário para transportar sua massa. A resistência surge contrária a
forças que atuem de maneira a rotacionar seu eixo de rotação a
qualquer configuração não paralela à sua posição original. Assim, um
veículo munido de um giroscópio e sensores apropriados pode medir
com precisão qualquer mudança em sua orientação, exceto rotações
que ocorram no plano de giro dos discos do giroscópio. Por essa
razão, normalmente são utilizados dois giroscópios perpendiculares de
modo a integralizar a possibilidade de detecção de variações na
orientação.
É usado como auxiliar em navegação de helicópteros radio
controlados, corrigindo automaticamente o curso.
As agências espaciais utilizam um aparelho baseado no
giroscópio conhecido como giroscópio humano para o treinamento de
astronautas. O astronauta utiliza o peso como motor e tem a sensação
de "driblar a gravidade". Somente depois de estar apto ao Giroscópio
humano o astrounauta estará pronto para fazer viagens espaciais.
L não pode ser
Adaptado de:
http://pt.wikipedia.org/wiki/Giroscópio
Sears & Zemansky, Young, Física, V 1, Ed. Pearson 10a Edição.
Giroscópio é um dispositivo que consiste de
um rotor suspenso
por
um
suporte
formado
por
dois circulos articulados, com juntas tipo cardan. Seu funcionamento
baseia-se no princípio da inércia. O eixo em rotação guarda direção
fixa em relação ao espaço. O giroscópio veio a substituir a bússola na
navegação marítima. Na aviação, serve de girocompasso e piloto
automático, permitindo o vôo em condições de visibilidade zero.
Nos vôos espaciais o dispositivo é fundamental para a
orientação das espaçonaves.
O giroscópio consiste essencialmente em uma roda livre,
ou varias rodas, para girar em qualquer direção e com uma
propriedade: opõe-se a qualquer tentativa de mudar sua direção
original. Exemplo facilmente observável é que, ao girar a roda de uma
bicicleta no ar e tentar mudar a direção de seu eixo bruscamente,
percebe-se uma enorme reação.
14
Física 1 – Capítulo 7 – Dinâmica do Movimento de Rotação – Prof. Dr. Cláudio Sérgio Sartori.
15