Binômio de Newton
1. (Uepg 2014) Sobre os polinômios P(x)  (2x  1)n e Q(x)  (2x  1)n , com n  *, assinale o
que for correto.
01) Se n  6, o termo médio de P(x) vale 40x3 .
02) A soma dos coeficientes de Q(x) é 1, qualquer que seja n.
04) Se n  4, então P(x)  Q(x) tem 3 termos.
08) Se n  10, o último termo de Q(x) é negativo.
16) Se n  5, então P(x)  Q(x) tem 10 termos.
2. (Uem 2014) Dados os inteiros não negativos n e k, sendo k  n, define-se o símbolo
n
n!
. Para cada inteiro n  1, considere pn  x  como sendo o polinômio
 
 k  k! n  k!
 n  n  n  n1  n  n2
n
n

 ...    x    .
 x  
x
x
n
 n  1
n  2
 1
0
Assinale o que for correto.
01) p4  x   x 4  4x3  6x2  4x  1.
02) Para todo inteiro n positivo, o polinômio pn (x) admite raízes não reais.
04) Para todos os valores de n, o polinômio pn (x) é divisível por x +1.
08) Para todo inteiro n > 2 , existem dois números racionais distintos, a e b , para os quais pn
(x) é divisível por x − a e por x − b .
16) Para cada inteiro positivo n, a soma de todos os coeficientes de pn (x) é 2n.
1
4
10
20
35
...
1
5
15
35
...
1
6
21
...
1
7
...
Coluna 7
1
3
6
10
15
21
...
Coluna 6
Coluna 3
1
2
3
4
5
6
7
...
Coluna 5
Coluna 2
1
1
1
1
1
1
1
1
...
Coluna 4
Coluna 1
Linha 0
Linha 1
Linha 2
Linha 3
Linha 4
Linha 5
Linha 6
Linha 7
...
Coluna 0
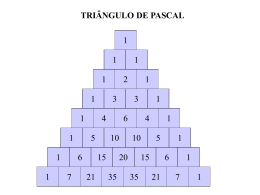
3. (Ufrgs 2014) Considere a configuração dos números dispostos nas colunas e linhas abaixo.
...
1
...
www.nsaulasparticulares.com.br
O número localizado na linha
15 e na coluna 13 é
a) 15.
b) 91.
c) 105.
d) 120.
e) 455.
Página 1 de 15
4. (Fgv 2013) Desenvolvendo-se o binômio P(x)  (x  1)5 , podemos dizer que a soma de seus
coeficientes é
a) 16
b) 24
c) 32
d) 40
e) 48
5. (Unioeste 2013) O valor da expressão
1534  4  1533  3  6  1532  32  4  153  33  34
é igual a
a) 153(153  3)3  3.
b) 1474.
c) 154  34.
d) 1534.
e) 154  104.
6. (Uern 2013) A soma dos algarismos do termo independente de x no desenvolvimento do
8
2

binômio de Newton   x  é
x


a) 3
b) 4
c) 6
d) 7
7
2

7. (Esc. Naval 2013) O coeficiente de x5 no desenvolvimento de   x3  é
x

a) 30
b) 90
c) 120
d) 270
e) 560
8. (Uepg 2013) Assinale o que for correto.
n  n 
01)    

 2 n  2
 4  4  4  4
02)             15
 1  2   3   4
 11  10   10 
04) A soma das soluções da equação         é 11.
x 3 2
 10   10 
08) A equação    
 tem duas soluções distintas.
 x   2x  4 
 n   n   n  1
16)       

 1  2   2 
www.nsaulasparticulares.com.br
Página 2 de 15
10
9. (Unioeste 2013) Seja f(x)  1 
 n!(10  n)! xn
10!
uma função real de variável real em que n!
n1
indica o fatorial de n.
Considere as afirmações:
I. f(0) = 0.
II. f(1) = 10.
III. f(−1) = 0.
Pode-se afirmar que
a) somente I é correta.
b) todas as afirmações são corretas.
c) II e III são corretas e I é incorreta.
d) III é correta e I e II são incorretas.
e) todas as afirmações são incorretas.
10. (G1 - ifal 2012) A expressão (x + y)n, com “n” natural, é conhecida como binômio de
Newton. Seu desenvolvimento é dado assim:
(x  y)n  Cn,0 xn y0  Cn,1xn1y1  Cn,p xnp yp  Cn,n xnn y
Por exemplo :
(x  y)3  C3,0 x3 y0  C3,1x31y1  C3,2 x3 2 y 2  C3,3 x3 3 y3 
 x3  3x 2 y  3xy 2  y3 .
Assim, a expressão 4x2 + 4xy + y2 corresponde a
a) C2,0 (2x)2 y0  C2,1(4x)1y1  C2,2 (2x)0 y2.
b) C2,0 (2x)2 y0  C2,1(2x)1y1  C2,2 (4x)0 y2.
c) C2,0 (x)2 y0  C2,1(2x)1y1  C2,2 (2x)0 y2.
d) C2,0 (4x)2 y0  C2,1(4x)1y1  C2,2 (4x)0 y2.
e) C2,0 (2x)2 y0  C2,1(2x)1y1  C2,2 (2x)0 y2.
12
1 

11. (Fgv 2012) O termo independente de x do desenvolvimento de  x 


x3 
a) 26.
b) 169.
c) 220.
d) 280.
e) 310.
é
n
 2

 x ,
12. (Uern 2012) Qual é o valor do termo independente de x do binômio 
2
x

considerando que o mesmo corresponde ao sétimo termo de seu desenvolvimento?
a) 435
b) 672
c) 543
d) 245
13. (Uespi 2012) Qual o coeficiente de x7 na expansão de (2  3x  x 2 )4 ?
a) 18
b) 16
c) 14
d) 12
e) 10
www.nsaulasparticulares.com.br
Página 3 de 15
14. (Ufpe 2012) Encontre o inteiro positivo n para o qual o quinto termo da expansão binomial
n
1

de  3 x   seja independente de x na expansão em potências decrescentes de x.

x
 (x  1)(5x  7) 
15. (Esc. Naval 2012) Seja m a menor raiz inteira da equação 
 !  1. Pode-se
3


afirmar que o termo médio do desenvolvimento de ( y  z3 )12m é
3
12! 18 2
a)
y z
6!6!
12! 3 18
b)
y z
6!6!
15
30!
c)
y 2 z45
15!15!
15
30! 2 45
y z
15!15!
12! 3 18
e)
y z
6!6!
d)
10
1

16. (Ufpe 2011) No desenvolvimento binomial de  1  
 3
inteiros?
, quantas parcelas são números
17. (Uepg 2011) Considerando que, a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 = 32 e a – b = –1,
assinale o que for correto.
01) a > 1.
02) b < 0.
b
04) é um número natural.
a
5
08) a2 + b2 = .
2
a 1
16)  .
b 3
18. (Uem 2011) Assinale o que for correto.
9
2

01) O coeficiente do termo x3 em  x   é - 672.
x

02)


2 1
x

 2  1 
x
 2  1
2  2 são maiores que 1.
04) Se x e y são números reais tais que y > x, então ay  ax , em que a é uma constante real
positiva.
08) A equação 4!Cx2,2  A x,3  0 possui exatamente duas soluções no conjunto dos números
inteiros maiores ou iguais a 4.
1
16) log 1 7   .
4
49
www.nsaulasparticulares.com.br
Página 4 de 15
n
3

No desenvolvimento  x 2   , n  , os coeficientes binominais do

x
quarto e do décimo terceiro termos são iguais. Então, o termo independente de x é o:
19. (G1 - ifal 2011)
a) décimo.
b) décimo-primeiro.
c) nono.
d) décimo-segundo.
e) oitavo.
20. (Uff 2010) Povos diferentes com escrita e símbolos diferentes podem descobrir um mesmo
resultado matemático. Por exemplo, a figura a seguir ilustra o Triângulo de Yang Yui, publicado
na China em 1303, que é equivalente ao Triângulo de Pascal, proposto por Blaise Pascal 352
anos depois.
Na expressão algébrica:
100
(x + 1)100 = a0 + a1 . x + a2 . x2 +...+a99 . x99 + a100 . x100 =
a
n
 xn
n 0
2
o coeficiente a2 de x é igual a:
a) 2
b) 100
c) 4950
d) 9900
e) 2100
21. (Ita 2010) A expressão (2 3  5 )5 – (2 3  5 )5 é igual a
a) 2630 5 .
b) 2690 5 .
c) 2712 5 .
d) 1584 15 .
e) 1604 15 .
www.nsaulasparticulares.com.br
Página 5 de 15
22. (Uff 2010)
Em computação gráfica, o sistema RGB identifica uma cor a partir de três números R, G e B
que especificam, respectivamente, as quantidades de vermelho (Red), verde (Green) e azul
(Blue) que compõem a cor. Outro sistema de identificação de cores é o NTSC (usado em TV).
Nesse sistema, uma cor também é definida por três números: Y (luminância), I (sinal em fase) e
Q (quadratura). Os dois sistemas estão relacionados através da seguinte equação matricial:
0,114  R 
 Y  0,299 0,587
 I   0,596 0,274 0,322 G
  
 
Q  0,211 0,523 0,312  B 
Se 0 ≤ R ≤ 1, 0 ≤ G ≤ 1 e 0 ≤ B ≤ 1, então
a) 0 ≤ Y ≤ 1, 0 ≤ / ≤ 1 e 0 ≤ Q ≤ 1
b) 0 ≤ Y ≤ 1, – 0,596 ≤ / ≤ 0,596 e – 0,523 ≤ Q ≤ 0,523
c) 0 ≤ Y ≤ 0,299, 0 ≤ / ≤ 0,596 e 0 ≤ Q ≤ 0,211
d) 0,114 ≤ Y ≤ 0,587, – 0,322 ≤ / ≤ 0,596 e – 0,523 ≤ Q ≤ 0,312
e) 0,211 ≤ Y ≤ 0,596, – 0,523 ≤ / ≤ 0,587 e – 0,322 ≤ Q ≤ 0,312
23. (Uel 1994) Se um dos termos do desenvolvimento do binômio (x + a) 5, com a ∈ IR, é 80x2,
então o valor de a é
a) 6
b) 5
c) 4
d) 3
e) 2
www.nsaulasparticulares.com.br
Página 6 de 15
Gabarito:
Resposta da questão 1:
02 + 04 = 06.
n
Os termos gerais de P e Q são, respectivamente, Tp1     2np  xnp e
p
n
Tq1  ( 1)q     2nq  xnq.
 q
[01] Incorreto. Se n  6, o termo médio de P(x) vale
6
T4     263  x 63
3
 20  8  x3
 160x3 .
[02] Correto. Tomando x  1, segue que a soma dos coeficientes de Q(x) é (2  1  1)n  1n  1,
qualquer que seja n.
[04] Correto. Se n  4, temos
 4
 4
 4
P(x)  Q(x)  2     24  x 4  2     22  x 2  2     20  x0
0
 2
 4
 32x 4  48x 2  2.
Portanto, P(x)  Q(x) tem 3 termos.
[08] Incorreto. Se n  10, então o último termo de Q(x) é
 10 
( 1)10     21010  x1010  1  0.
 10 
[16] Incorreto. Se n  5, então
P(x)  Q(x)  (2x  1)5  (2x  1)5
 [(2x  1)(2x  1)]5
 (4x 2  1)5 .
Por conseguinte, P(x)  Q(x) tem 5  1  6 termos.
Resposta da questão 2:
01 + 04 + 16 = 22.
[01] Verdadeira, pois x4 + 4x3 + 6x2 + 4x + 1 = (x + 1)4 e admite -1 como raiz.
[02] Falsa, para n = 2, P(x) = x2 + 2x + 1, possui duas raízes reais e iguais.
[04] Verdadeira, pois p(x) = (x + 1)n.
[08] Falsa, pois p(x) = (x +1 )n, portanto, a = b = - 1.
[16] Verdadeira, pois a soma dos coeficientes de (x + 1) n = (1 + 1)n = 2n.
www.nsaulasparticulares.com.br
Página 7 de 15
Resposta da questão 3:
[C]
A tabela acima é o famoso triângulo de Pascal.
 15 
15!
15  14

 105
 
2
 13  2! 13!
Resposta da questão 4:
[C]
A soma dos coeficientes de P é dada por
P(1)  (1  1)5  25  32.
Resposta da questão 5:
[E]
1534  4  1533  3  6  1532  32  4  153  33  34  (153  3)4  1504  154  104.
Resposta da questão 6:
[B]
O termo geral do binômio é
8 p
8  2 
Tp1      
 xp
p  x 
8!

 28p  x 2p8 .
p!  (8  p)!
O termo independente de x, se existir, é o natural p que torna o expoente de x igual a zero,
ou seja,
2p  8  0  p  4.
Em consequência, o termo independente de x existe e é igual a
T5 
8!
 28 4
4!  (8  4)!
8765 4
2
432
 1120.

Portanto, segue-se que o resultado é 1  1  2  0  4.
www.nsaulasparticulares.com.br
Página 8 de 15
Resposta da questão 7:
[E]
7p
 
7  2 
  
p  x 
 x3
p
7
    27p  x 4p7
p
Como o expoente de x é 5, temos 4p – 7 = 5, isto é p = 3. Fazendo, agora, p = 3, temos:
 7  73 437
x
 35  16  x5  560x5 .
 2
3
 
Portanto, o coeficiente pedido é 560.
Resposta da questão 8:
01 + 02 + 04 + 16 = 23.
[01] (Verdadeira), pois n - 2 + 2 = n (binomiais complementares).
 4  4  4  4
 4
[02] (Verdadeira).             24     15.
 1  2   3   4 
0
 11  10   10   11  11
[04] (Verdadeira).                x  3 ou x  3  11  x  2 ou x  8
x  3  2 x 3
e 8 + 3 = 11.
[08] (Falsa).
 10   10 
14
(não convém).
 
  2x  4  x ou 2x  4  x  10  x  4 ou x 
x
2x

4
3
  

 n   n   n  1
[16] (Verdadeira).       
 (relação de Stifel).
 1  2   2 
Resposta da questão 9:
[D]
10
f(x)  1 
 n!(10  n)! xn
10!
n1
n
f(x) 1  1  x   110
f (x)  1  x 
10
Então,
[I] f(0) = (1 + 0)10 = 1
[II] f(1) = (1 + 1)10 = 1024
[III] f(-1) = (1+(-1))10 = 0
Portanto, [III] é correta e [I] e [II] são incorretas.
Resposta da questão 10:
[E]
C2,0 (2x)2 y0  C2,1(2x)1y1  C2,2 (2x)0 y2  (2x  y)2  4x2  4xy  y 2
www.nsaulasparticulares.com.br
Página 9 de 15
Resposta da questão 11:
[C]
 
p  12 
 12 
O termo Geral do Binômio de Newton será dado por:   x12p  x 3     x124p
p
p
12
1 

Para que T seja o termo independente do desenvolvimento de  x 


x3 
12  4p  0  p  3
, devemos admitir
 12  12!
Logo, T    
 220
 3  3! 9!
Resposta da questão 12:
[B]
O termo geral do binômio é dado por
np
n  2 
Tp1     

 p   x2 
 xp
 n  2np
  
 xp
 p  x 2n2p
n
    2np  x3p 2n .
p
Sabendo que o termo independente de x é o sétimo, segue que p  6 e, assim,
n
T61     2n6  x182n .
6
Daí, impondo 18 – 2n = 0, concluímos que n = 9 e, portanto,
9!
987
9
T7     296 
 23 
 8  672.
6
6!

3!
32
 
Resposta da questão 13:
[D]
Reescrevendo o polinômio, obtemos
(2  3x  x 2 )4  
4!
 21  (3x)2  (x 2 )3
1!  2 !  3 !

4!
 21  32  x 2  23 .
1!  2 !  3 !
Para que o expoente de x seja 7, devemos ter 1  2  3  4 e 2  23  7. Desse modo,
como (1, 2, 3 )  (0,1, 3) é a única terna coordenada que satisfaz essas condições, temos
que o coeficiente de x 7 é dado por
4!
 20  31  12.
0!  1!  3!
www.nsaulasparticulares.com.br
Página 10 de 15
Resposta da questão 14:
16.
n
1

O termo geral do binômio  3 x   é dado por

x
n
Tk 1     ( 3 x )nk
k 
n
  x
k 
n
  x
k 
nk
3

k
 1
 
x
1
xk
n 4k
3 .
Sabendo que o quinto termo é independente de x, temos que k  4 e, portanto,
n 44
 0  n  16.
3
Resposta da questão 15:
[E]
Sabendo que 0!  1 e 1!  1, vem
(x  1)(5x  7)
7
 0  x  1 ou x 
3
5
ou
(x  1)(5x  7)
 1  5x 2  12x  4  0
3
2
 x  2 ou x  .
5
Donde concluímos que m  1.
Assim, como o termo geral de ( y  z3 )12 é
p
 12 
 12 
p
3 12p
 ( 1)12p   y 2 z363p ,
  ( y ) ( z )
p
p
e o termo médio é tal que
p 1
12
 1  p  6,
2
concluímos que o termo médio é igual a
6
 12 
12! 3 18
( 1)126   y 2 z3636 
y z .
6!6!
6
www.nsaulasparticulares.com.br
Página 11 de 15
Resposta da questão 16:
p
 10 
10!
1
 1
O termo geral do binômio é dado por Tp1     110p    
 p.


3
p!(10

p)!
p
3
 
Como 10!  10  9  8  7  6  5  4  3  2  34  10  8  7  2  5  4  2, segue que a maior potência de 3
que divide 10! é 34. Assim, p  {0, 1, 2, 3, 4}. Desses valores, os únicos que produzem parcelas
inteiras são 0 e 2. Portanto, duas parcelas do binômio dado são números inteiros.
Resposta da questão 17:
04 + 08 + 16 = 28.
Cálculos auxiliares
a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 = 32  (a + b)5 = 32  a + b = 2.
Portanto:
a  b  2

a  b  1

a 

b 

1
2
3
2
Item (01) – Falso
1
a  1
2
Item (02) – Falso
3
b 0
2
Item (04) – Verdadeiro
3
b  2 

 3 N
a  1
2
 
Item (08) – Verdadeiro
2
2
5
 1
3
a2  b2       
2
2
2
 
 
Item (16) – Verdadeiro
 1
a  2  1


b 3 3
2
 
www.nsaulasparticulares.com.br
Página 12 de 15
Resposta da questão 18:
01 + 08 + 16 = 25.
9
2

01) Correto. O termo geral do binômio  x   é dado por
x

9
Tk 1     x9k
k 
k
 2
 
 x
2k
9
    x9k  ( 1)k 
k 
xk
9
 ( 1)k  2k     x9 2k .
k 
Para determinarmos o coeficiente de x 3 devemos impor 9  2k  3  k  3.
Logo, o resultado pedido é
9!
9 3  8 4  7
9
( 1)3  23     8 
 8 
 672.
3!  6!
3 1  2 1
3
02) Incorreto. Fazendo ( 2  1)x  y, y  * , segue que
y
2 1
 2  2  y 2  ( 2  2)y  2  1  0
y
y
2 2 2
2
 y  2  1 ou y  1.
Portanto, como ( 2  1)x  2  1  x  1 e ( 2  1)x  1  x  0, temos que nenhuma das
raízes da equação é maior do que 1.
04) Incorreto. Se 0  a  1 e y  x, então ay  ax , sendo a uma constante real positiva.
08) Correto. Temos que
4!Cx 2,2  A x,3  0  4! 
(x  2)!
x!

0
2!  (x  4)! (x  3)!
 4  3  (x  2)  (x  3)  x  (x  1)  (x  2)  0
 (x  2)  (  x 2  13x  36)  0
 (x  2)  (x  4)(x  9)  0
 x  4 ou x  9.
Note que o conjunto universo das soluções da equação dada é {x  | x  4}.
16) Correto. Temos que log 1
49
7  log
72
1
2
7
1 1
1
    log7 7   .
2 2
4
www.nsaulasparticulares.com.br
Página 13 de 15
Resposta da questão 19:
[B]
p
n
n
3

3
O termo geral do binômio  x 2   é Tp1     (x 2 )np    .

x
x
p
Se os coeficientes binominais do quarto e do décimo terceiro termos são iguais, então
n  n 
      n  3  12  15.
 3   12 
Logo,
p
 15 
3
Tp1     (x 2 )15p   
p
x
 
 15 
3p
    x302p  p
x
p
 15 
    x303p  3p
p
Como o desenvolvimento do binômio apresenta um termo independente de x, deve-se ter
30  3p  0  p  10.
Portanto, o termo pedido é o décimo primeiro.
Resposta da questão 20:
[C]
100  100 p 100 p
 x
T  
.1
 p 
100  p  2  p  98, fazendo p  98 temos :
100  2 98
.x .1  T  4950 x 2
T  
 98 
Logo o coeficiente de x2 é 4950.
Resposta da questão 21:
[B]
Utilizando o Binômio de Newton, temos
(a + b) 5 = a5 + 5.a4.b+10.a 3.b2 + 10.a 2.b2 + 5.a.b4 + b5
(a - b) 5 = a5 - 5.a4.b + 10.a 3.b2 - 10.a 2.b2 + 5.a.b4 - b5
(a + b) 5 - (a - b) 5 = 10a 4.b + 20.a 2.b3 + 2b5
Logo:
2
2
2
 
5   2
5   2
5
  10.(2 3) . 5  20.(2 3) .
5   1440 5  1200 5  50 5
5   2690 5
3 5  2 3 5
3
3
5
3
5
3
5
4
2
3
5  2. 5
5
5
5
www.nsaulasparticulares.com.br
Página 14 de 15
Resposta da questão 22:
[B]
Multiplicando as matrizes temos:
0,114 B 
Y  0,299 R 0,587]G
 I   0,596 R  0,274G  0,322 B 
  

O   0,211R  0,523G 0,312 B 
Menor Y = 0,299.0 + 0,587.0 + 0,114.0 = 0
Maior Y = 0,299.1 + 0,587.1 + 0,114.1 = 1
Menor I = 0,596.0 – 0,274.1 – 0,322.1 = - 0,596
Maior I = 0,596.1 – 0,274.0 – 0,322.0 = 0,596
Menor O = 0,211.0 - 0,523.1 + 0,312.0 = - 0,523
Maior O = 0,211.1 - 0,523.0 + 0,312.1 = 0,523
Resposta da questão 23:
[E]
www.nsaulasparticulares.com.br
Página 15 de 15