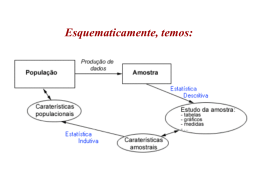
ESTATÍSTICA
Ciências Contábeis
Professor: Ricardo Vojta
RAMOS DA ESTATÍSTICA
A estatística dedutiva (também conhecida como
Estatística Descritiva) se encarrega de descrever
o conjunto de dado desde a elaboração da
pesquisa até o cálculo de determinada medida.
A estatística indutiva (ou Estatística Inferencial)
está relacionada a incerteza. Inicia-se no cálculo
das Probabilidades e se desenvolve por todo a
área da inferência.
1 – ESTATÍSTICA DESCRITIVA
- Variáveis
- População e Amostra
- Técnicas de Amostragem
- Séries Estatísticas
- Gráficos Estatísticos
- Distribuição de Freqüências
MÉTODO ESTATÍSTICO
- MÉTODO: conjunto de meios dispostos convenientemente
para se chegar a um fim que se deseja
1.MÉTODO EXPERIMENTAL: consiste em manter
constantes todas as causas (fatores), menos uma, e variar esta
causa de modo que o pesquisador possa descobrir seus efeitos,
caso existam.
2.MÉTODO ESTATÍSTICO: diante da impossibilidade de
manter as causas constantes, admite todas essas causas
presentes variando-as, registrando essas variações e
procurando determinar, no resultado final, que influências
cabem a cada uma delas.
ESTATÍSTICA
Def.: é a parte da matemática aplicada que fornece
métodos para a coleta, organização, descrição, análise e
interpretação de dados e para a utilização dos mesmos na
tomada de decisões.
FASES DO MÉTODO ESTATÍSTICO
1 – Coleta de dados: pode ser direta ou indireta.
a) Direta: quando feita sobre elementos informativos de
registro obrigatório ou coletados pelo próprio
pesquisador. Essa coleta pode ser contínua, periódica
ou ocasional.
b) Indireta: quando é feita com base em elementos já
pesquisados (revista, jornal, livros, etc.)
2- Crítica dos dados: nesta fase os dados são contados e
recontados, em busca de possíveis falhas (omissões,
repetições, etc), sendo:
a) Externa: informante
b) Interna: pesquisador
3- Apuração dos dados: é a soma e o processamento dos
dados obtidos. Pode ser manual, eletromecânica ou
eletrônica.
4 – Apresentação dos dados: os dados devem ser
apresentados sob a forma de tabelas e gráficos.
5 – Análise dos resultados: o objetivo último da
Estatística é tirar conclusões sobre o todo a partir de
informações fornecidas por uma parte deste
representativa, através de técnicas apropriadas
RESUMO
COLETA
DE DADOS
CRÍTICA
DOS DADOS
APURAÇÃO DOS DADOS
TABELAS
GRÁFICOS
ANÁLISE DE
RESULTADOS
VARIÁVEL: é, convencionalmente, o conjunto de
resultados possíveis de um fenômeno.
1.Qualitativa:
1.1 – Nominal: quando seus valores são expressos por
atributos. Ex.: cor dos olhos, da pele, do cabelo, religião,
sexo, tipo de condução, curso de graduação,
nacionalidade, naturalidade, etc.
1.2 – Ordinal: quando, apesar de não poder ser medida, a
variável segue uma ordem. Ex.: escolaridade, patente
militar, cargos dentro de uma empresa, hierarquia no
serviço público civil, etc.
2.Quantitativa: quando as variáveis são expressas em
números, e podem ser:
2.1 –Discretas: resultam de um conjunto enumerável de
valores (aceita apenas números inteiros). Ex.: quantidade
de carros no estacionamento, número de filhos de um
casal, quantidade de cursos de uma faculdade, etc.
2.2 – Contínuas: quando uma variável pode assumir
qualquer valor entre dois limites (valores inteiros e
decimais). Ex.: faixa etária, horas, faixa salarial,
comprimento, temperatura, peso, altura, etc.
POPULAÇÃO, AMOSTRA e AMOSTRAGEM
POPULAÇÃO: É um conjunto de indivíduos ou
objetos que apresentam pelo menos uma
característica em comum.
AMOSTRA: Considerando a impossibilidade, na
maioria das vezes do tratamento de todos os
elementos da população, necessitaremos de uma parte
representativa da mesma. A esta porção da população
chamaremos de amostra.
AMOSTRAGEM: é uma técnica especial para recolher
amostras que garante, tanto quanto possível, o acaso na
escolha, de modo a garantir à amostra o caráter de
representatividade.
TÉCNICAS DE AMOSTRAGEM
1. Casual ou Aleatória Simples: equivalente a um sorteio, é
utilizada quando a população encontra-se desordenada, sendo que
por essa técnica, qualquer elemento tem a mesma chance de ser
sorteado.
- Quando a população é relativamente pequena (até 30, por
exemplo), pode-se numerar os elementos e em seguida, realizar o
sorteio.
- Tratando-se de uma quantidade grande, o processo de
numeração torna-se trabalhoso. Para tanto, utiliza-se a TABELA
DE NÚMEROS ALEÁTORIOS (TNA).
-A leitura dessa tabela é feita, após escolhido o ponto de início, da
esquerda para a direita e vice-versa, de cima para baixo e viceversa, na diagonal, etc. A opção deve ser feita antes de iniciado o
processo.
Ex.: Suponhamos que uma amostra deverá ter 12 elementos de
uma população total de 90 indivíduos, e que se tenha escolhido
começar na primeira linha da Tabela de Números Aleatórios
(TNA), partindo da esquerda para a direita. O primeiro número
escolhido seria 57, o segundo 72, e a seqüência seria:
57 - 72 - 00 - 39 - 84 - 84 - 41 - 79 - 67 - 71 - 40 - 21 - 13
97 - 56 - 49 - 86 - 54 - 08 - 93 - 29 - 68 - 74 - 54 - 83
Destes números sorteados seriam utilizados os 12 primeiros:
57 - 72 - 39 - 84 - 41 - 79 - 67 - 71 - 40 - 21 - 13 - 56
Se o procedimento escolhido fosse da direita para esquerda, os
elementos utilizados:
83 - 54 - 74 - 68 - 29 - 08 - 86 - 49 - 56 - 13 - 21 - 40
2. SISTEMÁTICA - novamente é feito o sorteio, sendo que
nessa amostragem os elementos da população já se encontram
ordenados e, nesses casos, não é necessário se construir um
sistema de referência (TNA).
Exemplos de populações ordenadas: fichas individuais de
empregados (alfabética), casas de uma rua (número), notas
fiscais (data), etc.
Ex.: Suponhamos que uma empresa tenha 720 colaboradores
em determinado setor, dentre os quais deseja-se uma amostra
formada por 30 destes empregados
Procedimento:
1.Determinar o intervalo de amostragem.
população
Intervalo =
amostra
Þ
720
30
Þ
Intervalo = 24
2.Escolhemos, por sorteio, um número de 01 a 24 (inclusive).
Este número indicará o primeiro elemento da amostra
3. Se o primeiro número sorteado for o 5, escolhemos os demais
colaboradores relacionado com o primeiro elemento da amostra:
2.º ® 5 + 24 = 29.º
3.º ® 29 + 24 = 53.º
4.º ® 53 + 24 = 77.º
Os demais elementos serão escolhidos, periodicamente, em
intervalos de 24 em 24.
3. ESTRATIFICADA PROPORCIONAL: utilizada quando
a população encontra-se dividida em estratos (ou camadas,
faixas, intervalos, etc).
Exemplos de populações divididas em estratos
-sexo (homem e mulher);
- idade (criança, adolescente, adulto e idoso);
- setores de uma empresa (administração, vendas, tesouraria,
serviços gerais, etc)
-Cursos de uma faculdade (C. Contábeis, Administração,
Direito, Enfermagem, etc);
-Faixa salarial (até 1 SM, de 1 a 2 SM, de 2 a 4 SM, acima de
4 salários-mínimos).
Obs.: após a escolha da quantidade de elementos por
estrato, será utilizado o sorteio (simples ou TNA) para
determinar os indivíduos que comporão a amostra.
Ex.: Será realizada uma pesquisa, a partir de uma
amostra, de 12 pessoas. Essa pessoas compõem um
grupo de 94 que farão parte de uma expedição na
Amazônia, sendo: 45 argentinos, 18 bolivianos e 31
colombianos. Determinar a quantidade de pessoas de
cada nacionalidade que responderá a pesquisa
Resolução:
Calcula-se primeiramente percentual da amostra:
amostra
%amostra =
´ 100
população
Þ
Estrato
População
(Nacionalidade)
12
´100 Þ
94
%amostra = 12,766%
Cálculo
Proporcional
Valor
Amostra
6
2
Argentina
45
45´12,766%
5,745
Boliviana
18
18´ 12,766%
2,298
Colombiana
31
31´12,766%
3,957
Total
94
__
__
4
12
Questão 1: A Prefeitura Municipal de Santarém tem 450 moto-taxistas oficiais.
Obtenha uma amostra representativa (aleatória simples), correspondendo a 4%
do total. Utilize a TNA, a partir da 2.ª linha, da esquerda para a direita
Questão 2: Uma rede de franquia possui 240 pontos, (numerados de 001 até
240) em todo território brasileiro. Desejando-se saber como está o nível de
satisfação de seus franqueados, será realizada uma pesquisa com 20 desses
pontos. Determine quais pontos serão selecionados para a amostra, sendo que
o primeiro é o de n.º 7 e que a técnica utilizada é a amostragem sistemática.
Questão 3: Suponha que determinada faculdade tenha 5 cursos de graduação,
assim distribuídos: 175 alunos em Administração, 153 em Biologia, 141 em
Contabilidade, 249 em Direito e 295 em Enfermagem. Uma pesquisa será
realizada com 50 acadêmicos. Determine, pela técnica de amostragem
estratificada, a quantidade de alunos de cada curso que comporão a amostra.
Ex.:Uma empresa apresenta o seguinte quadro relativo às suas
filiais em seis diferentes cidades do Pará:
Filial
homens
mulheres
Alenquer
80
95
Itaituba
102
120
Juruti
110
92
Monte Alegre
134
228
Oriximiná
150
130
Santarém
300
290
total
Total
Obtenha uma amostra proporcional estratificada de 120 estudantes
Resolução:
%amostra =
amostra
´ 100
população
Þ 120 ´100 Þ
1831
%amostra = 6,554%
Cálculo proporcional
escola
homens
mulheres
amostra
total
homens
mulheres
total
homens
mulheres
total
A
80
95
195
5,243
6,226 11,469
5
6
B
102
120
6,685
7,865 14,550
7
8
C
110
92
222
202
11
15
7
6
13
D
134
228
362
6,029 13,238
8,782 14,943 23,725
9
15
24
E
160
120
280
7,865
18,351
10
8
18
F
300
290
19,661 19,006
19
39
886
945
38,667
__
20
totais
590
1831
58
62
120
7,209
10,486
58,067 61,933
NORMAS PARA CONSTRUÇÃO DE TABELAS
TABELAS ESTATÍSTICAS
- Um dos objetivos da estatística é sintetizar os valores
que uma ou mais variáveis podem assumir, para que
tenhamos uma visão global da variação das mesmas.
Tabela é uma maneira de apresentar de forma resumida
um conjunto de dados.
ELEMENTOS DE UMA TABELA
TÍTULO (o quê ?; onde ?; quando ?)
Coluna
Coluna
Coluna
indicadora
numérica 1
numérica 2
Cabeçalho
casa ou célula
linhas
rodapé : fonte, notas, chamadas
TÍTULO DA TABELA
Conjunto de informações, as mais completas possíveis, respondendo
às perguntas: O que?, Quando? E Onde?, localizado no topo da
tabela, além de conter a palavra “TABELA” e sua respectiva
numeração.
CORPO DA TABELA: é o conjunto de Linhas e Colunas que
contém informações sobre a variável em estudo.
a) Cabeçalho da Coluna – Parte superior da tabela que especifica o conteúdo
das colunas;
b) Coluna Indicadora – Parte da tabela que especifica o conteúdo das linhas;
c) Linhas – retas imaginárias que facilitam a leitura, no sentido horizontal, de
dados que se inscrevem nos seus cruzamentos com as linhas;
d) Casa ou Célula – espaço destinado a um só número;
e) Total – deve ser SEMPRE destacado de alguma forma;
f) Laterais da tabela – não devem ser fechadas. Caso as feche, passa a ser
chamada de “QUADRO”.
g) Número – preferencialmente utilizar separador de 1000 (por exemplo:
1.854.985 ao invés de 1854985).
Há ainda a considerar os elementos complementares da tabela,
que são a fonte, as notas, e as chamadas, localizadas, de preferência,
no rodapé.
a) Fonte – identifica o responsável (pessoa física ou jurídica) ou
responsável pelos dados numéricos;
b) Notas – é o texto que irá esclarecer o conteúdo estudado, que
poderá ser de caráter geral ou específico de uma tabela;
c) Chamadas – símbolo remissivo atribuído a algum elemento de
uma tabela que necessita de uma nota específica.