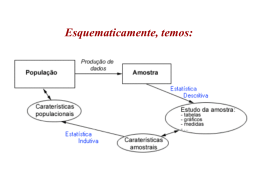
Estatística Aplicada ao Serviço Social
Módulo 1:
Introdução à Estatística
Importância da Estatística
Fases do Método Estatístico
Variáveis estatísticas.
Formas Iniciais de Tratamento dos Dados
Séries Estatísticas.
Apresentação de Dados – Gráficos e Tabelas
ESTATÍSTICA.
Estatística é método cientifico que permite organizar dados, analisá-los e
tomar decisões em condições de incerteza.
A coleta, a organização, a descrição dos dados, o cálculo e a interpretação de
coeficientes pertencem à ESTATÍSTICA DESCRITIVA enquanto a análise e a
interpretação dos dados, associado a uma margem de incerteza, ficam a cargo
da ESTATÍSTICA INDUTIVA ou INFERENCIAL, também chamada como
medida da incerteza ou métodos que se fundamentam na teoria da
probabilidade.
POPULAÇÃO E AMOSTRA
População é um conjunto de elementos com uma característica comum.
O termo é mais amplo no senso comum, pois envolve aglomerado de pessoas,
objetos ou mesmo idéias. Exemplo: todos os alunos de uma faculdade.
Amostra são subconjuntos da população que conservam, portanto, a
característica comum da população é retirada por técnicas adequadas,
chamadas de amostragem. Exemplo 50 alunos de uma faculdade.
Variáveis ou parâmetros são características numéricas da população.
Exemplo notas dos alunos da faculdade.
VARIÁVEIS ESTATÍSTICAS
Variável é o conjunto de resultados possíveis de um fenômeno. As variáveis
estatísticas podem ser qualitativas ou quantitativas
Variáveis qualitativas são as que expressão atributos (qualidades) e podem
ser nominais ou ordinais. As ordinais possuem uma ordem natural enquanto
que as nominais não.
Exemplo: sexo, cor, raça são vaiáveis qualitativas nominais enquanto que grau
de escolaridade, faixa etária (criança, adolescente, adulto e idoso) são
variáveis qualitativas ordinais.
Variáveis quantitativas são as que expressão valores numéricos, ou seja,
quantidade. As variáveis quantitativas podem ser discretas (só admite valores
inteiros) ou continuas (podem ser fracionadas ou seja apresenta continuidade).
Exemplo: quantidade aluno de uma sala, número de defeitos em aparelhos de
TV são vaiáveis quantitativas discretas enquanto que peso de pessoas,
produção de café no Brasil são variáveis quantitativas continuas.
TECNICAS DE AMOSTRAGEM
Amostragem aleatória ou causal simples.
A amostra é escolhida de forma que todos os elementos da população
possuem a mesma chance.
Exemplo: alunos escolhidos por sorteio para responder um teste.
Amostragem sistemática.
Quando os elementos da população já se acham ordenados, não há
necessidade de construir o sistema de referência. São exemplos os prontuários
médicos de um hospital, os prédios de uma rua, etc. Nestes casos, a seleção
dos elementos que constituirão a amostra pode ser feita por um sistema
imposto pelo pesquisador.
Exemplo: Suponhamos uma rua com 900 casas, das quais desejamos obter
uma amostra formada por 50 casas para uma pesquisa de opinião. Podemos,
neste caso, usar o seguinte procedimento: como 900/50 = 18, escolhemos por
sorteio casual um número de 01 a 18, o qual indicaria o primeiro elemento
sorteado para a amostra; os demais elementos seriam periodicamente
considerados de 18 em 18. Assim, suponhamos que o número sorteado fosse
4 a amostra seria: 4ª casa, 22ª casa, 40ª casa, 58ª casa, 76ª casa, etc.
Amostragem proporcional estratificada.
Quando a população se divide em estratos (sub-populações), convém que o
sorteio dos elementos da amostra leve em consideração tais estratos, daí
obtemos os elementos da amostra proporcional ao número de elementos
desses estratos.
Exemplo: Vamos obter uma amostra proporcional estratificada, de 10%,
supondo, que, numa classe de 90 alunos, 54 sejam meninos e 36 sejam
meninas. São, portanto dois estratos (sexo masculino e sexo feminino). Logo,
temos:
SEXO POPULACÃO
10 %
AMOSTRA
MASC.
54
5,4
5
FEMIN.
36
3,6
4
Total
90
9,0
9
Numeramos então os alunos de 01 a 90, sendo 01 a 54 meninos e 55 a 90,
meninas e procedemos o sorteio casual com urna ou tabela de números
aleatórios.
Amostragem por conveniência.
Quando é usado como amostra um cadastro já existente ou grupo de fácil
pesquisa. Exemplo: ficha de empregados de uma empresa, alunos de uma
sala de aula.
ARREDONDAMENTO DE DADOS
Quando o primeiro algarismo a ser abandonado for 0, 1, 2, 3 ou 4, fica último
algarismo a permanecer.
Exemplo: Arredondando para uma casa decimal 53,24 passa a 53,2
Quando o primeiro algarismo a ser abandonado for 5, 6, 7, 8, ou 9, aumenta-se
de uma unidade o algarismo a permanecer.
Exemplos: Arredondando para uma casa decimal 42,87 passa a 42,9; 2,352
passa a 2,4 e 24,75 passa a 24,8
Apresentação de Dados em Tabela e Gráficos
Tabela é um quadro que resume um conjunto de dados dispostos segundo
linhas e colunas de maneira sistemática.
De acordo com a Resolução 886 do IBGE, nas casas ou células da tabela
devemos colocar:
um traço horizontal ( - ) quando o valor é zero;
três pontos ( ... ) quando não temos os dados;
zero ( 0 ) quando o valor é muito pequeno para ser expresso pela unidade
utilizada;
um ponto de interrogação ( ? ) quando temos dúvida quanto à exatidão de
determinado valor.
Obs: O lado direito e esquerdo de uma tabela oficial deve ser aberto.
COMPONENTES DE UMA TABELA
Título é o conjunto de informações localizado no topo da tabela
Corpo é o conjunto de linhas e colunas que contém informações sobre a
variável em estudo.
Cabeçalho parte superior que especifica o conteúdo das colunas.
Coluna indicadora especifica o conteúdo das linhas.
Casas ou células espaço destinado a um só número.
Obs: No rodapé de uma tabela podem aparecer informações complementares
que são:
Fonte que indica a procedência dos dados
Notas que são informações complementares
Chamadas que são observações especificadas sobre um ou alguns dados.
TABELA DE DUPLA ENTRADA OU SÉRIES CONJUGADAS
É sua usada quando temos a necessidade de apresentar em uma única tabela,
a variação de valores de mais de uma variável.
Exemplo:
Tipo sanguíneo e fator Rh dos funcionários da indústria X
Tipos sanguíneos
Fator Rh
O
A
B
AB Total
Positivo
156
139
37
12
344
Negativo
28
25
8
4
65
Total
184
164
45
16
409
GRÁFICOS ESTATÍSTICOS
São representações visuais dos dados estatísticos que devem corresponder,
mas nunca substituir as tabelas estatísticas. Os gráficos devem ter
simplicidade, clareza e veracidade.
Alguns gráficos podem transmitir uma idéia falsa dos dados que estão sendo
analisados, chegando mesmo a confundir o leitor. Trata-se, na realidade, de
um problema de construção de escalas.
Os gráficos mais utilizados em estatísticas são os seguintes:
Gráficos em barras horizontais.
Gráficos em barras verticais (colunas).
Gráficos em barras compostas.
Gráficos em colunas superpostas.
Gráficos em linhas ou lineares.
Gráficos em setores (Pizza).
Pictogramas (São construídos a partir de figuras representativas da
intensidade do fenômeno. Este tipo de gráfico tem a vantagem de despertar a
atenção do público leigo, pois sua forma é atraente e sugestiva.)
Exercício Resolvido - 1
Considerando a série estatística abaixo, complete as porcentagens com uma
casa decimal e fazendo a compensação, se necessário.
Alunos
Séries
%
matriculados
1ª
546
2ª
328
3ª
280
4ª
120
Total
1274
Solução:
Para fazermos o cálculo das porcentagens podemos usar a regra pratica:
(valor  total).100%
(546  1274).100% = 42,8571% fazendo o arredondamento temos 42,9%
(328  1274).100% = 25,7456% fazendo o arredondamento temos 25,7%
(280  1274).100% = 21,9780% fazendo o arredondamento temos 22,0%
(120  1274).100% = 9,4191% fazendo o arredondamento temos 9,4%
O total das porcentagens deve fechar em 100,0%.
Conferindo 42,9 + 25,7 + 22,0 + 9,4 = 100,0%. Então não há necessidade de
fazer a compensação.
Completando a tabela temos:
Alunos
Séries
matriculados
1ª
546
2ª
328
3ª
280
4ª
120
Total
1274
%
42,9
25,7
22,0
9,4
100
Exercício Resolvido - 2
Para convencer a população local da ineficiência da Companhia Telefônica
Vilatel na expansão da oferta de linhas, um político publicou no jornal local o
gráfico 1, abaixo representado. A Companhia Vilatel respondeu publicando dias
depois o gráfico II, onde pretende justificar um grande aumento na oferta de
linhas. O fato é que, no período considerado, foram instaladas, efetivamente,
200 novas linhas telefônicas.
Analisando os gráficos, pode-se concluir que
a) o gráfico II representa um crescimento real maior do que o do gráfico 1.
b) o gráfico I apresenta o crescimento real, sendo o II incorreto.
c) o gráfico II apresenta o crescimento real, sendo o gráfico 1 incorreto.
d) a aparente diferença de crescimento nos dois gráficos decorre da escolha
das diferentes escalas.
e) os dois gráficos são incomparáveis, pois usam escalas diferentes.
Solução:
Os dois gráficos contem o mesmo tipo de informação. A aprente diferença é
devido a escala, portanto o item correto é da alternativa D
Exercícios propostos
Exercício 1
Um determinado curso de uma faculdade possui 450 alunos sendo que 125
alunos cursam o 1º ano; 115 alunos cursam o 2º ano, 108 alunos cursam o 3°
ano e 102 alunos cursam o 4º ano. O coordenador do curso deseja fazer uma
pesquisa entrevistando os alunos. Como não dispõe de tempo para entrevistar
todos resolveu fazer por amostragem estratificada de 12%. Determine a
quantidade de alunos a ser entrevistados no total e por ano.
Exercício 2
Abaixo temos variáveis qualitativas e quantitativas. Assinale a alternativa que
corresponde à variável qualitativa:
a) População: alunos de uma escola.
Variável: cor dos cabelos
b) População: casais residentes em uma cidade.
Variável: número de filhos
c) População: as jogadas de um dado.
Variável: o ponto obtido em cada face
d) População: peças produzidas por certa máquina.
Variável: número de peças produzidas por hora
e) População: peças produzidas por certa máquina.
Variável: diâmetro externo
Exercício 3
Quando uma variável é quantitativa como ela pode se apresentar
a) Contensiva ou Discrepante
b) Caracterizada ou Personalizada
c) Contínua ou Discreta
d) Contensiva ou Discreta
e) Contínua ou Discrepante
Exercício 4
Quando dizemos que chegamos a uma conclusão partindo da observação de
partes de um todo, estamos falando sobre?
a) População
b) Amostra
c) Censo
d) Pesquisa
e) Resto
Referência bibliográfica: Bibliografia básica e complementar da disciplina