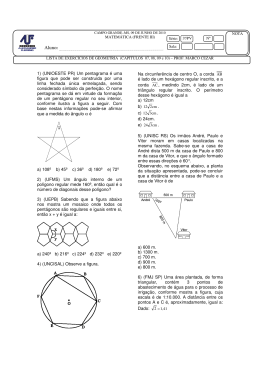
Aluno(a):_____________________________________________________________ Código:__|__|__|__|__
Série: 3ª  Turma: _______
Data: ___/___/___
04. Dois robôs, a e B, trafegam sobre um plano cartesiano. Suponha que
2
no instante t suas posições são dadas pelos pares ordenados sA (t) = (t, –t
+ 3t + 10) e sB (t) = (t, 2t + 9), respectivamente.
Sabendo que os robôs começam a se mover em t = 0,
1. DETERMINE o instante t em que o robô a se chocará com o robô B .
01. Num dado momento, três canais de TV tinham, em sua programação,
novelas em seus horários nobres: a novela A no canal A, a novela B no
canal B e a novela C no canal C. Numa pesquisa com 3000 pessoas,
perguntou-se quais novelas agradavam. A tabela a seguir indica o número
de telespectadores que designaram as novelas como agradáveis.
Gab:
Número de
telespectadores
A
1450
B
1150
C
900
AeB
350
AeC
400
BeC
300
A, B e C
100
t
Novelas
1 5
2
2. Suponha que haja um terceiro robô C cuja posição é dada por sc (t) = (t,
kt + 11) , em que k é um número real positivo.
DETERMINE o maior valor de k para que a trajetória do robô C intercepte
a trajetória do robô a.
Quantos telespectadores entrevistados não acham agradável
nenhuma das três novelas?
Gab:
kmáx = 1
Gab: 450
02. No dia 17 de Maio próximo passado, houve uma campanha de doação
de sangue no campos da Universidade de Fortaleza. Sabemos que o
sangue das pessoas pode ser classificado em quatro tipos quanto a
antígenos. Uma pesquisa feita com um grupo de 100 alunos da
Universidade constatou que 42 deles têm o antígeno A, 36 têm o
antígeno B e 12 o antígeno AB. Sendo assim, determine o número de
alunos cujo sangue tem o antígeno O.
05. A distância entre duas retas paralelas é o comprimento do segmento
de perpendicular às retas que tem uma extremidade em uma reta e a
outra extremidade na outra reta.
No plano cartesiano, calcule a distância entre as retas de equações
3x + 4y = 0 e 3x + 4y + 10 = 0.
Gab: 2
Gab: 34
06. Um frasco em forma de um cone circular reto com boca de 8 cm de
diâmetro e 16 cm de altura contém um líquido até a altura de 10 cm,
conforme mostra a figura.
03. Foi aplicado um teste contendo três questões para um grupo de 80
alunos. O gráfico abaixo representa a porcentagem de acerto dos alunos
por questão.
3
Considerando  = 3, determine o volume de líquido, em cm , que
ainda precisa ser colocado dentro desse cone para completar sua
capacidade máxima.
Suponha que 52 alunos acertaram pelo menos duas questões e 8
alunos não acertaram nenhuma. Calcule o número de alunos que
acertaram as três questões.
Gab: 12
Gab: 193,5
2
Rua T-53 Qd. 92 Lt. 10/11 nº 1356 – Setor Bueno – 62-3285-7473 – www.milleniumclasse.com.br
07. A figura a seguir representa uma garrafa cheia de vinho e uma taça,
em formato de cone, com suas respectivas medidas.
i
Q
Δt
 i
10N  1020
n e
Δt
 n
i Δt
0,4  60

e
1,6  1019
 n  1,5  1020.
 N  20.
12. Ao ser conectado a uma rede elétrica que fornece uma tensão eficaz
de 200 V, a taxa de consumo de energia de um resistor ôhmico é igual a
60 W. Determine o consumo de energia, em kWh, desse resistor, durante
quatro horas, ao ser conectado a uma rede que fornece uma tensão
eficaz de 100 V.
Dados nominais fornecidos no enunciado:
U  200V P  60w
De acordo com os dados apresentados, determine no máximo
quantas taças que essa garrafa serve.
A partir destes dados, temos:
E  P  Δt  15.103 kω  4 h neste resistor é dada por:
U2
1002
3.10000


R
2000
 2000 
 3 


30
P
 P  15w
2
Gab: cinco taças cheias
P
08. Em um reservatório cilíndrico, com 2 metros de diâmetro, foram
colocados 12 000 litros de água, fazendo com que a água atingisse 80%
da altura total do reservatório. Considerando  = 3, determine a altura,
em metros, desse reservatório.
Gab: 5
A energia consumida em 4 horas é dada por:
09. Um silo para armazenamento de cereais é formado pela junção de um
cilindro e um cone com o mesmo raio da base e dimensões internas
indicadas na figura a seguir. Determine quantos metros cúbicos de
cereais podem ser armazenados neste silo. (Adote  = 3,14)
E  P  Δt  15.103 kw   4 h
 E  0,06kwh
13. Uma câmara escura de orifício reproduz uma imagem de 10 cm de
altura de uma árvore observada. Se reduzirmos em 15 m a distância
horizontal da câmara à árvore, essa imagem passa a ter altura de 15 cm
Gab: 3454
10. Um reservatório tem a forma de uma esfera. Se aumentarmos o raio
da esfera em 20%, calcule o aumento percentual do volume do novo
reservatório, em relação ao volume inicial.
Gab: 72,8%
a) Qual é a distância horizontal inicial da árvore à câmara?
ANTES:
11. Um fio metálico e cilíndrico é percorrido por uma corrente elétrica
constante de 0,4 A. Considere o módulo da carga do elétron igual a
-19
1,6 x 10 C Expressando a ordem de grandeza do número de elétrons de
condução que atravessam uma seção transversal do fio em 60 segundos
N
na forma 10 , qual o valor de N?
DEPOIS:
Da definição de corrente elétrica:
3
Rua T-53 Qd. 92 Lt. 10/11 nº 1356 – Setor Bueno – 62-3285-7473 – www.milleniumclasse.com.br
Nessa figura nota-se que o eclipse anelar do Sol ocorre
quando a Lua está mais afastada do observador, ou seja, a
Lua está no apogeu.
6
3
b) Sabendo que o raio do Sol é 0,70 x 10 km, o da Lua, 1,75 x 10 km, e
que a distância entre o centro do Sol e o observador na Terra é de 150 x
6
10 km, calcule a distância d entre o observador e o centro da Lua para a
qual ocorre o eclipse total indicado na figura.
H  10cm 
 H.d  10D
Dd

H  15cm 
 H.d  15(D  15)
D  15m  d
Dados: RS = 0,70  106 km; RL = 1,75  103 km, dS = 150  106
km.
10D  15(D  15)
10D  15D  225
5D  225
 D  45m
b) Ao se diminuir o comprimento da câmara, porém mantendo seu
orifício à mesma distância da árvore, o que ocorre com a imagem
formada? Justifique.
Da semelhança de triângulos na figura:
d
d
 S
RL RS
A imagem irá diminuir. Observe a justificativa:
d
150  106

3
1,75  10
0,7  106

d
1,75  106  150
0,7

H  h
 H.d  h.D
D  d
h

d = 3,75  105 km.
H.d
D
15. Um menino de 1,5 m de altura produz uma sombra de 50 cm. No
mesmo instante, um prédio próximo ao menino produz uma sombra de
20 m. Calcule a altura do prédio, em metros.
Dados: h = 1,5 m; d = 50 cm = 0,5 m; D = 20 m.
Note que para “H” e “D” constantes a “h” é diretamente
proporcional a “d”, ou seja se “d” diminui “h” também
diminui. Vale salientar que apesar da imagem diminuir ela
ficará mais nítida sobre a tela, uma vez que, a mesma
intensidade luminosa será projetada em uma área menor,
aumentado a nitidez.
H D
H
20
 H = 1,5 (40)  H = 60 m.



h d
1,5 0,5
16. O gráfico mostra a variação da corrente elétrica I, em ampère, num
fio em função do tempo t, em segundos. Qual a carga elétrica, em
coulomb, que passa por uma seção transversal do condutor nos
primeiros 4,0 segundos?
14. A figura a seguir (evidentemente fora de escala) mostra o ponto O em
que está o olho de um observador da Terra olhando um eclipse solar
total, isto é, aquele no qual a Lua impede toda luz do Sol de chegar ao
observador.
a) Para que o eclipse seja anelar, isto é, para que a Lua impeça a visão dos
raios emitidos por uma parte central do Sol, mas permita a visão da luz
emitida pelo restante do Sol, a Lua deve estar mais próxima ou mais
afastada do observador do que na situação da figura? Justifique sua
resposta com palavras ou com um desenho.
Portanto:
Justificando com um desenho. A figura mostra a posição da
Lua relativamente à Terra e ao Sol, em dois tipos de eclipse
do Sol: total e anelar.
Q
 4  1
2
 4  Q  10 C.
4
Rua T-53 Qd. 92 Lt. 10/11 nº 1356 – Setor Bueno – 62-3285-7473 – www.milleniumclasse.com.br
17.
No arranjo experimental da figura, os corpos A e B têm massas,
respectivamente, iguais a 2,0 kg e 3,0 kg. Despreze atritos e as massas do
2
fio e da polia. Adote g = 10,0 m/s .
Considerando que os corpos são abandonados em repouso, calcule
os trabalhos realizados pelos pesos dos corpos A e B sobre os respectivos
corpos durante o primeiro segundo de movimento.
a = 2m/s2
20 J e 30 J
18. Considere um ferro elétrico que tem uma resistência elétrica de 22Ù e
fica ligado duas horas por dia a uma voltagem de 110 V.
a) Qual o valor da corrente elétrica que passa por este ferro elétrico?
GAB: 5A
b) Qual o consumo de energia elétrica (em kWh) deste ferro ao longo de
30 dias?
33kWh
19. Na brincadeira conhecida como cabo de guerra, dois grupos de
palhaços utilizam uma corda ideal que apresenta um nó no seu ponto
mediano. O gráfico a seguir mostra a variação da intensidade da
resultante F das forças aplicadas sobre o nó, em função da sua posição x.
Considere que a força resultante e o deslocamento sejam paralelos.
Determine o trabalho realizado por F no deslocamento entre 2,0 e 9,0m.
GAB: 190 J
20. Uma criança de 20kg parte do repouso no topo de um escorregador a
2,0m de altura. Sua velocidade quando chega à base é de 6,0m/s. Qual foi
o módulo do trabalho realizado pelas forças de atrito, em joules?
GAB: 40
5
Rua T-53 Qd. 92 Lt. 10/11 nº 1356 – Setor Bueno – 62-3285-7473 – www.milleniumclasse.com.br