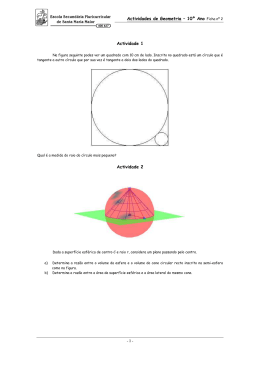
Inscrição e circunscrição de
sólidos geométricos
Esfera e cubo
Esfera e cilindro
Esfera e cone reto
Cilindro e cone reto
Introdução
Nosso último estudo em Geometria será
destinado aos sólidos inscritos e
circunscritos.
Existem numerosas relações entre dois
sólido quando construímos um deles dentro
do outro.
São algumas dessas relações que
estudaremos a partir de agora.
Esfera e cubo
Considere uma esfera cujo
o raio mede R inscrita em
um cubo cujas arestas têm
medida a.
Existe uma relação entre as
medidas das arestas do
cubo e do raio da esfera.
Como a superfície esférica
intersecta o cubo em seis
pontos, localizados nos
centros das faces, temos
três pares de pontos
diametralmente opostos.
Assim, a medida de cada
aresta do cubo é igual ao
dobro da medida do raio da
esfera.
a = 2.R
Esfera e cubo
Considere um cubo
cujas arestas medem
A, inscrito em uma
esfera cujo o raio tem
medida R:
Observe que os vértices do
cubo pertencem à superfície
esférica.
Assim, a medida da
diagonal do cubo é igual ao
dobro da medida do raio da
esfera.
Dcubo = 2.R
a. 3 = 2.R
Esfera e cubo
Para você fazer – p. 34
1) Uma esfera está inscrita em um cubo cujo o
volume é igual a 64 dm³. Calcule o volume
da esfera.
Sendo " a" a medida das arestas do cubo, temos que a 3 = 64dm →
a = 4dm
Assim, a medida do raio da esfera é a = 2.R, portanto, R = 2 dm,
4
e seu volume é igual Vesfera = πR 3 , então :
3
4
Vesfera = .π 23
3
esfera
V
32π
3
dm
=
3
Esfera e cubo
Para você fazer – p. 34
2) Uma esfera, cuja área da superfície mede
192πcm², circunscreve um cubo. Calcule o
volume desse cubo.
Sendo R a medida do raio da esfera, temos que 4π .R 2 = 192π → R = 4 3cm
Sendo " a" a medida das arestas do cubo, temos a 3 = 4.2 3 → a = 8cm
Assim, o volume do cubo é igual a 8 = 512cm
3
3
Esfera e cilindro
Considere uma esfera cujo
raio mede R inscrita em um
cilindro reto.
Como a superfície intersecta
as bases do cilindro nos
seus centros, e o círculo
máximo da esfera é
congruente às bases do
cilindro, então as medidas
do raio e da altura do
cilindro são iguais,
respectivamente, a R e 2R,
ou seja o cilindro é
equilátero.
Esfera e cilindro
Nesse caso como podemos
estabelecer uma relação entre
as medidas do raio da esfera,
do raio do cilindro e da altura
do cilindro?
Observe a figura a seguir:
2R
h
No triângulo retângulo,
de catetos medindo h e
2r, onde h e r são as
medidas da altura e do
raio do cilindro, e da
hipotenusa medindo
2R, podemos escrever:
(2R )2 = (2r )2 + h 2
4 R = 4r + h
2
2r
2
2
Esfera e cilindro
Para você fazer – p. 35
Uma esfera está inscrita em um cilindro cuja altura mede
10cm. Calcule o volume compreendido entre o cilindro e a
esfera.
Resposta:
Se a altura do cilindro mede 10cm, então o raio da base
desse cilindro e o raio da esfera medem 5 cm.
Assim, o volume compreendido entre o cilindro e a esfera é
igual a
1)
Vesfera − Vcilindro
4
500π
3
π .5 .10 − .π .5 = 250π −
3
3
2
250π
3
Vt =
cm
3
Esfera e cilindro
Para você fazer – p. 35
2) Em uma esfera, está inscrita um cilindro reto cuja altura mede
20 cm e cujo raio da base mede 8cm. Calcule a área da
superfície dessa esfera.
Na figura, temos que (2R ) = (20) + 16 2 → 4 R 2 = 400 + 256 → R 2 = 164
2
2
→ R = 2 41 cm.
(
)
A área da superfície da esfera é igual a 4π . 2 41 = 656π cm 2
2
Esfera e cone reto
Da mesma forma como o cubo
e o cilindro, em uma cone
também é possível inscrever ou
circunscrever uma esfera.
Vamos, inicialmente, considerar
uma esfera de raio r inscrita em
um cone de raio R e altura h.
Sendo g a medida da
geratriz do cone, podemos,
por meio de uma
semelhança de triângulos,
estabelecer a seguinte
proporção
r h−r
=
R
g
Esfera e cone reto
Se o cone for equilátero,
não há necessidade de
utilizar a proporção anterior.
Basta lembrar que a medida
do raio da esfera é igual 1/3
da medida da altura do
cone, ou seja, h = 3r
Assim, por meio do
Teorema de Pitágoras,
temos:
(2 R )2 = R 2 + (3r )2
→ 4 R 2 = R 2 + 9r 2
→ 3R 2 = 9r 2
R=r 3
Esfera e cone reto
Agora, considere uma esfera de raio R,
circunscrevendo um cone de raio r e altura h.
No triângulo retângulo em destaque,
podemos escrever :
R = r + (h − r )
2
2
2
Esfera e cone reto
Existem outras relações
entre as medidas do raio da
esfera da base do cone, da
altura e da geratriz do cone.
Porém, não existe
necessidade de conhecêlas, pois, por meio da
relação anterior, podemos
obter quaisquer outras
medidas.
Se o cone é equilátero, a
media do raio é igual a 2/3
da medida da altura do
cone, ou seja, h = 3R/2.
Logo, por meio do Teorema
de Pitágoras, temos:
(2r )2 = r 2 +  3R 
 2 
2
9
R
4r 2 = r 2 +
4
9R 2
2
3r =
4
2
3
R
r2 =
4
2
R 3
r=
2
Esfera e cone reto
Para você fazer – p. 36
1)
Uma esfera está inscrita em um cone reto
cuja altura mede 8cm e cujo raio da base
mede 6cm. Calcule o volume dessa esfera.
Sendo g a medida da geratriz do cone, temos que g2 = 62 + 82 → g = 10cm
Sendo R a medida do raio da esfera, temos, por meio de uma semelhança
de triângulos, que :
R 8 −R
=
→ 10R = 48 − 6R → R = 3cm
6
10
Assim, o volume da esfera é igual a
4
.π .33 = 36π cm3
3
Esfera e cone reto
Para você fazer – p. 36
2) Em um cone equilátero, cujo volume é igual 72π√3 cm³, inscreve-se
uma esfera. Calcule a área da superfície dessa esfera.
Em um cone equilátero , a medida da geratriz é igual ao dobro da media
do raio.
Assim, sendo h a medida da altura do cone, temos que :
(2R )2 = R 2 + h 2 → h = R
3
Como o volume do cone é igual a 72π 3cm 3, temos :
1
72π 3 = .π .R 2 .R 3 → 216 = R 3 → R = 6cm
3
Assim, a medida da altura do cone é 6 3 cm e, como a medida do raio
da esfera é igual a terça parte da medida da altura do cone, o raio da esfera
mede 2 3
(
)
A área da superfície esférica é igual a 4π . 2 3 = 48πcm3
2
Esfera e cone reto
Para você fazer – p. 36
3) Um cone equilátero está inscrito em uma
esfera cujo volume mede 288π m³. Calcule a
área lateral desse cone.
Sendo R a medida do raio da esfera, temos
4
.π .R 3 = 288π → R 3 = 216 → R = 6cm
3
2
2
h → 6 = h → h = 9m
3
3
2
Sendo r a medida do raio da base cone equilátero , então (2R ) = R 2 + h 2
Sendo h a medida da altura do cone, temos R =
(2.6 )2 = r 2 + 9 2 → r 2 = 27 → r = 3
3m
Assim, a área lateral do cone é igual a π .r.g = π .3 3.6 3 = 54π m 2
Cilindro e cone retos
Considere um cilindro
de altura h e raio da
base R.
Inscrevendo-se nele
um cone reto, temos a
seguinte figura:
Note que o vértice do cone coincide com o centro de uma das bases do
cilindro, e a base do cone coincide com a outra base do cilindro.
Assim, os raios das bases do cone e do cilindro são, evidentemente,
congruentes, da mesma forma que as medidas das alturas.
Cilindro e cone retos
Observe um cilindro reto, com raio da base r
e altura h, inscrito em um cone reto de raio
da base R e altura H.
Cilindro e cone retos
H-h
g
G
r
H
Gg
h
h
r
R-r
R
Cilindro e cone retos
Pela semelhança existente entre três triângulos da
figura, podemos escrever as seguintes proporções:
Tomando II e I, temos
II
r H −r g
=
=
R
H
G
Tomando II e III, temos
r
H −r
g
=
=
R -r
h
G−g
I
III
Tomando III e I, temos
R -r h G − g
=
=
R
H
G
Cilindro e cone retos
Para você fazer – p. 37
Se um cilindro cuja altura mede 10cm está inscrito em cone
reto cuja geratriz mede 25 e com raio da base medindo 20 cm,
calcule o volume desse cilindro.
Para calcular o volume, temos :
Vcilindro = π .R 2 .h
Sendo h a medida da altura do cone,
temos que :
25 2 = 20 2 + h 2 → h = 15cm
Por meio de uma semelhança
de triângulo, podemos :
r H −r
r 15 − 10
20
=
→
=
→r =
cm
R
H
20
15
3
Assim o volume, temos :
Vcilindro
4000π
=
cm3
9
Vcilindro
2
4000π
 20 
= π .R 2 .h = π .  .10 =
9
 3 
Resolução de Atividades
Página 37 e 38
Nota livre - Vestibulares
Parabéns, chegamos
ao fim da Geometria