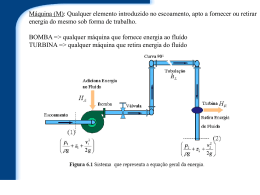
AULA 02 - DESEMPENHO DAS BOMBAS CENTRÍFUGAS
1 Objetivos
Determinar o ponto de trabalho de uma bomba centrífuga: vazão, altura
manométrica, potência consumida e eficiência.
2 Características do sistema de bombeamento.
Para determinar o ponto de trabalho de uma bomba é necessário
determinar a energia por unidade de peso que o sistema irá solicitar da bomba,
em função da vazão bombeada. Essa energia que o sistema exige recebe o
nome de altura manométrica do sistema.
2.1
Altura manométrica de um sistema ( )
A altura manométrica de um sistema em função da vazão é uma
característica particular de cada sistema. Este parâmetro depende da altura
estática de elevação do fluido, das diferenças de pressão entre sucção e
descarga e das perdas de carga do sistema. A Figura 1 apresenta um sistema
de bombeamento genérico:
Figura 1 - Sistema de Bombeamento
Para uma determinada vazão, a bomba da Figura 1 deve fornecer carga
suficiente para suprir a altura manométrica solicitada pelo sistema, ou seja,
deverá compensar a altura geométrica (
), compensar as diferenças
de pressão (
) e compensar todas as perdas de carga na linha.
2.2
Cálculo da Altura Manométrica de um sistema de bombeamento
A altura manométrica é a energia por unidade de peso que um sistema
solicita de uma bomba para uma determinada vazão e é calculada através da
expressão:
[
]
(Eq. 1)
Onde,
= energia já existente no flange de sucção. Corresponde a energia do
ponto 1 na Figura 1. Nesse ponto do sistema, as partículas de fluidos que se
deslocaram do reservatório de sucção já experimentaram a perda de carga nas
tubulações de sucção. Logo, essa energia é a energia existente na sucção.
= energia que deverá existir no flange de descarga. Corresponde a
energia do ponto 2 na Figura 1. Nesse ponto do sistema, as partículas de
fluidos ainda irão se deslocar da saída da bomba para o reservatório de
descarga e ainda não experimentaram a perda de carga nas tubulações de
descarga. Logo, essa energia é a energia deve existir na descarga para que as
partículas de fluido tenham condições de vencer as perdas de cargas e chegar
ao reservatório de descarga.
O cálculo da altura manométrica total do sistema pode ser feito em partes,
ou seja, primeiro calcula-se a energia na sucção e descarga separadamente e
em seguida, utiliza-se a Equação 1 para calcular a altura total. Inicialmente,
para determinar a altura manométrica da bomba no lado da sucção, deve-se
partir da equação de carga de um fluido aplicada na entrada da bomba:
(Eq. 2)
Onde,

= carga de pressão

= carga cinética

= carga potencial
Primeiramente, deve-se alinhar o eixo cartesiano xy com o eixo da
bomba, para conhecer as alturas de elevação existentes no sistema. Em
seguida, é necessário analisar no ponto observado a existência ou não de
pressão e velocidade. Por último, decidimos quais parcelas de carga serão
consideradas no cálculo da altura manométrica em cada ponto.
Para ilustrar o uso da Equação 2, será considerado o sistema de
bombeamento da Figura 2. O cálculo da altura manométrica no ponto b da
Figura 2 fornece exatamente a energia por unidade de peso no flange de
sucção da bomba. Vemos que as partículas de fluido que atravessam este
ponto estão no mesmo nível do eixo da bomba. Logo, a altura estática de
elevação nesse ponto é nula. A velocidade e a pressão do fluido nesse ponto
não devem ser desprezadas, já que o escoamento está em curso.
Figura 2 - Cálculo de hs
Vemos que no flange da bomba as parcelas de carga que compõem a
energia por unidade de peso no ponto b da Figura 2 são apenas em relação às
cargas cinéticas e de pressão. Dessa forma, a altura manométrica na sucção
pode ser dada pela seguinte expressão:
(Eq. 3)
Para o cálculo da altura manométrica diretamente no flange de sucção da
bomba é necessário conhecer a altura estática, pressão e vazão, com o auxilio
de algum tipo de instrumentação básica. Se na pratica não houver como
determinar tais parâmetros, é possível determinar a altura manométrica
considerando as condições do reservatório de sucção, através do uso da
equação de Bernoulli:
(Eq. 4)
A Equação 4 indica que entre duas seções num escoamento qualquer, as
energias nos pontos 1 e 2 serão iguais, se durante o trajeto as partículas de
fluido não perderem energia (carga) devido ao atrito. Na prática, o atrito da
parede dos tubos e demais acessórios da tubulação impõem perdas de carga
ao escoamento, e as energias dos pontos 1 e 2 não serão iguais. Então, para
calcular a energia no flange de sucção de uma bomba a partir dos dados do
reservatório é necessário considerar as perdas de carga ao longo do trajeto a
ser percorrido pelo fluido.
Considerando o exemplo dado na Figura 2, devemos escrever a equação
de Bernoulli entre os pontos a e b:
(Eq. 5)
No ponto a da Figura 2 foi considerado que a parcela de carga cinética é
nula, pois a velocidade das partículas de fluido na lamina d’água é desprezível,
pois as dimensões do reservatórios são muito maiores que a dimensão das
tubulações. No ponto b (flange de sucção da bomba) a parcela de carga
potencial também foi desprezada, uma vez que o eixo da bomba está na
mesma cota de altura de elevação que as partículas de fluido nesse ponto. O
termo
representa a perda de carga que ocorre no escoamento quando o
fluido se desloca do ponto a ao ponto b do sistema.
Somamos a perda de carga à energia do ponto b, pois no ponto b a
energia é menor que a energia do ponto a proporcionalmente à perda de carga
na sucção. Para que as energias entre esses dois pontos sejam iguais é
necessário somar a perda de carga ao valor da carga do ponto b, equilibrando
a energia entre os dois pontos.
Considerando que a altura manométrica no flange de sucção é dada pela
Equação 3, podemos substituir este resultado na Equação 5. Rearrumando os
termos, temos:
(Eq. 6)
E finalmente:
(Eq. 7)
A Equação 7 é equivalente a Equação 3, porém a Equação 3 foi deduzida
conhecendo os valores das parcelas de carga no flange de sucção da bomba e
a equação 7 foi deduzida aplicando a Equação de Bernoulli entre o reservatório
de sucção e o flange de sucção da bomba.
Para determinar a energia no flange de descarga ( ), basta seguir o
mesmo raciocínio considerado para calcular a energia no flange de sucção da
bomba.
3 Altura Manométrica Total - Curva do Sistema
Para determinar a altura manométrica total do sistema é necessário
determinar as condições de energia associada à carga do fluido nos flanges de
descarga e sucção da bomba. A energia total do sistema então é calculada
através da Equação1. Sabemos que existem duas maneiras de determinar a
energia no flange de sucção ou descarga: conhecendo as parcelas de carga na
entrada ou saída da bomba ou aplicando a equação de Bernoulli a partir do
reservatório de sucção ou descarga até o ponto desejado.
Assim, observando a Figura 1 novamente, a Equação 1 pode assumir as
formas abaixo:
(Eq. 8)
ou,
(Eq. 9)
Na Equação 9, o termo que contabiliza a carga cinética foi desprezado,
pois as dimensões dos reservatórios de sucção e descarga são bem maiores
que o diâmetro das tubulações. Ainda na Equação 9, temos que os termos
referentes as perdas de carga são afetados pela velocidade do escoamento e
aumentam com o aumento da velocidade. Se as dimensões da tubulação são
constantes, quanto maior a vazão de bombeamento, maior será a perda de
carga total.
Podemos ver que pressão e altura estática são cargas não influenciadas
pela velocidade do escoamento. Então, aumentando a vazão, aumentamos a
perda de carga, e aumentamos também a energia que o sistema irá solicitar da
bomba. Calculando a altura manométrica do sistema para vários valores de
vazão, podemos traçar a curva característica do sistema, que mostra a
variação de altura manométrica total em função da vazão, conforme a Figura 3:
Figura 3 - Curva do Sistema H x Q
4
Ponto de Trabalho
Para localizar o ponto de trabalho de uma bomba, basta cruzar as curvas H
x Q da bomba e do sistema, de acordo com a Figura 4. O ponto de interseção
entre estas duas curvas é o ponto de trabalho, indicando uma vazão de
trabalho ( ) e uma altura manométrica total de trabalho ( ). A curva H x Q do
sistema é calculada pelo projetista do sistema de bombeamento e a curva H x
Q da bomba é sempre fornecida pelo fabricante do equipamento.
O ponto de trabalho determina que se a bomba operar na vazão de
trabalho, o equipamento está operando com segurança. Normalmente, os
fabricantes também fornecem as curvas de desempenho de potência (
) e
rendimento ( ). Podemos identificar qual a potência e o rendimento da bomba
quando a mesma estiver operando na vazão de trabalho, pela interseção das
curvas de desempenho ( e
) com a linha vertical que passa pelo ponto de
trabalho.
Figura 4 – Ponto de Trabalho