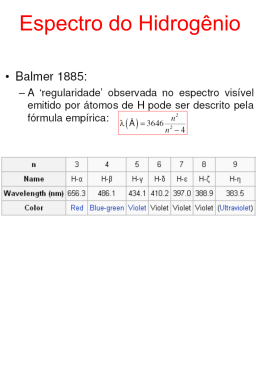
Capítulo 40
Mais ondas de matéria
40.1 A estrutura dos átomos
Inicio séc. XX
estrutura átomo?
1926 física quântica
Partículas = ondas de matéria
Eq. de Schroedinger
40.2 Ondas em cordas e ondas de
matéria
Confinamento

quantização
Estados discretos
Energias discretas
“O confinamento de uma onda leva à quantização, ou seja, à
existência de estados discretos com energias discretas. A onda
pode ter apenas uma destas energias.”
40.3 Energia de um elétron
confinado
Ondas em cordas:
Armadilhas unidimensionais
V  -
V=0
V  -
x
L
x=0
x=L
U(x)
x
0 L
Cálculo das energias quantizadas
De Broglie
(onda de matéria)
3o. Estado excitado
2o. Estado excitado
1o. Estado excitado
Estado fundamental
L=0.39 nm
Poço de potencial infinito
Mudanças de energia
E
emissão
E4
Emissão ou absorção de fótons:
E3
absorção
E2
E1
Verificação
Coloque em ordem os seguintes pares de estados quânticos de um
elétron confinado a um poço unidimensional infinito de acordo
com as diferenças de energia entre os estados, começando pela
maior: (a) n = 3 e n = 1; (b) n = 5 e n = 4; (c) n = 4 e n = 3.
(a)
(b)
(c)
Portanto (b) > (a) > (c)
Exercícios e Problemas
11P. Um elétron está confinado em um poço de potencial infinito
unidimensional de 250 pm de largura e se encontra no estado
fundamental. Quais são os quatro maiores comprimentos de onda
que podem ser absorvidos pelo elétron de uma só vez?
E
E5
E4
E3
E2
E1
40.4 Funções de onda de um
elétron aprisionado
Resolvendo eq. de Schroedinger:
para
Probabilidade de detecção
Probabilidade p(x) de
detecção no intervalo
dx com centro em x
Probabilidade de
detecção entre x1 e x2
=
=
Densidade de
probabilidade y2n(x)
no ponto x
(Intervalo dx )
n=2
n=1
0
50
100
0
x (pm)
50
100
x (pm)
n = 15
n=3
0
50
x (pm)
100
0
50
x (pm)
100
Princípio da correspondência
“Para grandes valores dos números quânticos, os resultados da física
quântica tendem para os resultados da física clássica.”
n = 15
0
50
x (pm)
100
0
50
x (pm)
100
Verificação
A figura abaixo mostra três poços infinitos de potencial de
largura L, 2L e 3L; cada poço contém um elétron no estado
n=10. Coloque os poços na ordem (a) do número máximo de
máximos da densidade de probabilidade do elétron, começando
pelo maior; (b) na ordem das energias do elétron, começando
pela maior.
L
2L
3L
Normalização
Partícula em algum lugar do espaço, logo:
Ex.:
Energia de ponto zero
Menor valor para n é 1, portanto menor energia é:
“Em sistemas confinados não existem estados de energia zero.”
Verificação
As partículas a seguir estão confinadas em poços de potencial
infinitos de mesma largura: (a) um elétron, (b) um próton, (c) um
deuteron e (d) uma partícula alfa. Coloque as partículas na ordem das
energias de ponto zero, começando pela maior.
40.5 Um elétron em um poço
finito
Poço infinito = idealização
Poço finito = mais realista
U
U(x)
U0
x
0
Equação de Schrödinger:
L
L
E (eV)
n=3
Não-quantizada
450
Alto do poço
E3=280 eV
n=2
E2=109 eV
n=1
E1=24 eV
0
0
x (pm)
100
U0 = 450 eV
L = 100 pm
Exercícios e Problemas
19E. Um elétron no estado n = 2 do poço de potencial finito da Fig.
40.7 absorve uma energia de 400 eV de uma fonte externa. Qual é a
energia cinética do elétron após esta absorção, supondo que o
elétron seja transferido para uma posição onde x > L?
U
U(x)
U0 = 450 eV
L = 100 pm
U0
x
0
L
E (eV)
Não-quantizada
450
Alto do poço
E3=280 eV
E2=109 eV
E1=24 eV
0
U0 = 450 eV
L = 100 pm
40.6 Outras armadilhas para
elétrons
Nanocristalitos
CdSe
Pontos quânticos
Auto-organizados
Pontos quânticos
Pontos quânticos
Estruturados
Currais quânticos
Átomos de Fe sobre cobre
40.7 Armadilhas eletrônicas
bidimensionais e tridimensionais
1-D
2-D
periodic in
one direction
periodic in
two directions
3-D
periodic in
three directions
Curral retangular (2D)
z
curral
y
Lx
Ly
x
Verificação
Na notação da equação abaixo, a energia do estado fundamental
do elétron em uma caixa retangular é E0,0 ; E1,0 ; E0,1 ou E1,1?
nx, ny = 1, 2, 3, …
Caixa retangular (3D)
z
Lz
y
Lx
Ly
x
Exercícios e Problemas
26P. Um curral retangular de larguras Lx=L e Ly=2L contém um
elétron. Determine, em múltiplos de h2/8mL2, onde m é a massa do
elétron, (a) a energia do estado fundamental do elétron, (b) a energia
do primeiro estado excitado, (c) a energia dos primeiros estados
degenerados e (d) a diferença entre as energias do segundo e do
terceiro estado excitado.
(a)
(b)
(c)
(d)
40.8 O átomo de hidrogênio
ep+
Energia (eV)
Energias dos estados do átomo de
hidrogênio
Distância radial (Å)
A teoria de Bohr do átomo de
hidrogênio
Números quânticos do átomo de
hidrogênio
Módulo do momento angular orbital
Orientação no espaço do momento angular orbital
Verificação
(a) Um grupo de estados quânticos do átomo de hidrogênio tem
n = 5. Quantos valores de l são possíveis para os estados do
grupo? (b) Um subgrupo de estados do átomo de hidrogênio
dentro do grupo n = 5 tem l = 3. Quantos valores de ml são
possíveis para os estados deste subgrupo?
A função de onda do estado
fundamental do átomo de hidrogênio
Estado fundamental:
a é o raio de Bohr:
Densidade de probabilidade
radial, estado fundamental
Estados do átomo de hidrogênio
com n = 2
Estados do átomo de hidrogênio
com n = 2
Estados do átomo de hidrogênio
com n = 3
Estados do átomo de hidrogênio
com n = 3
Estados do átomo de hidrogênio
com n = 3
Exercícios e Problemas
43P. Um fóton com um comprimento de onda de 486,1 nm é
emitido por um átomo de hidrogênio. (a) Que transição do átomo é
responsável por esta emissão? (b) A que série pertence esta
transição?
Série de Lyman
Série de Balmer
Perguntas
1. Quando multiplicamos por 2 a largura de um poço de potencial
infinito unidimensional, (a) a energia do estado fundamental do
elétron confinado é multiplicada por que número? (b) As energias
dos outros estados são multiplicadas por este número ou por algum
outro, que depende do número quântico?
Perguntas
2. Três elétrons são aprisionados em três diferentes poços de
potencial infinitos unidimensionais de largura (a) 50 pm, (b) 200
pm e (c) 100 pm. Coloque os elétrons na ordem das energias dos
estados fundamentais, começando pela maior?
Perguntas
3. Se o leitor quisesse usar a armadilha idealizada da figura abaixo
para capturar um pósitron, teria que mudar (a) a geometria da
armadilha, (b) o potencial elétrico do cilindro do meio ou (c) os
potenciais elétricos dos cilindros das extremidades? (O pósitron é
uma partícula de carga positiva com a mesma massa que o elétron).
V  -
V=0
V  -
L
x=0
x=L
Perguntas
4. Um elétron confinado em um poço de potencial infinito
unidimensional se encontra no estado n = 17. Quantos pontos de (a)
probabilidade zero e (b) probabilidade máxima; possui a onda de
matéria associada ao elétron?
n=2
n=1
0
50
100
0
x (pm)
50
100
x (pm)
n = 15
n=3
0
50
x (pm)
100
0
50
x (pm)
100