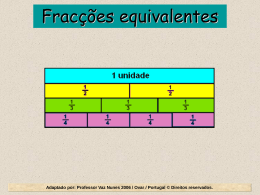
NÚMEROS RACIONAIS
FRACÇÕES
A Joana e o André parece terem voltado ao
tempo da pré-primária! Toda a tarde a fazer
figurinhas, pintar, contar … que giro!
Afinal, já estão no 6º Ano! Estão a trabalhar
com números racionais, fracções … sei lá …
nomes esquisitos ! ! !
Anda ! Vamos espreitar!
eh..eh!!?
Escreve para cada caso a fracção que representa a porção pintada.
2
3
1
4
3
2
4
4
5
4
8
8
3
6
4
3
3
3
Ah!...
Muito bem! Afinal tu também gostas destas brincadeiras…
Então, agora, responde-me tu, a ver se sabes:
De todas aquelas fracções, quais as que representam
números menores que 1? Números menores que a unidade?
2
3
1
4
3
6
Parabéns! Está correcto.
Concluímos que: Quando o numerador é menor que o
denominador, a fracção representa um número menor que
1.Chamam-se FRACÇÕES PRÓPRIAS.
E quais daquelas fracções representam números maiores que 1?
Números maiores que a unidade?
3
2
4
3
5
4
Parabéns, outra vez!
Concluímos que: quando o numerador é maior que o denominador, a
fracção representa um número maior que 1. Chamam-se FRACÇÕES
IMPRÓPRIAS.
E quais representam o número 1?
Representam a unidade?
4
4
8
8
3
3
Parabéns, pela 3ª vez!
Concluímos que: Uma fracção representa o número 1 (a unidade)
quando o numerador é igual ao denominador.
Agora vou eu brincar contigo! Queres?
Considera as fracções:
Descobre as duas
fracções que são
“intrusas” neste grupo.
1
2
5
100
8
1000
Pois é… também acertaste. As intrusas são:
25
10
3
4
96
10
12
1000
1 e 3
2
4
As outras são: FRACÇÕES DECIMAIS, ou seja, fracções
cujo denominador é 10, 100, 1000… (potência de base
10).
312
100
Mais um desafio para ti:
Escreve sob a forma de numeral decimal, o número representado por cada
uma das fracções decimais.
96

10
25

10
5

100
12

1000
312

100
Fracções com igual denominador….
Na festa de anos da Joana, todos os bolos estavam
cortados em doze fatias iguais. O gráfico refere-se ao
número de fatias de cada bolo, que se comeu durante a
festa.
12
Chocolate
Nº de fatias comidas
10
Amêndoa
8
6
Noz
4
2
0
Escreve a fracção correspondente ao número de fatias que se comeu
de cada bolo.
Amêndoas
8
12
Chocolate
11
12
Noz
4
12
11 8
4


12 12 12
Conclusão: Fracções com igual denominador, representa um número
maior a que tiver maior numerador.
Fracções com igual numerador…
A mãe do André pôs-lhe um problema: tenho uma barra de chocolate
para repartir por duas, três ou quatro crianças. Em que caso, ficará cada
criança com mais chocolate?
O André pensou, fez um esquema e depois respondeu.
1
2
1
3
1
4
Quando são só duas crianças.
1 1 1
 
2 3 4
Concordas com o André?
Conclusão: Fracções com igual numerador, é maior a que tiver menor
denominador.
E se as fracções tiverem diferentes numeradores e diferentes
denominadores? Como fazer?
2
1
é maior ou menor que
?
4
5
É fácil !!!
2
 2 : 4  0,5
4
1
 1 : 5  0,2
5
0,5  0,2
Logo
2 1

4 5
Podemos dividir o numerador pelo denominador e comparar os resultados.
FRACÕES EQUIVALENTES
A Educadora deu a cada um dos meninos: Zezinho, Pedrinho e Joãozinho,
uma folha A4 para pintarem como se fosse uma parede.
1
2
4
O Zezinho pintou
da folha, o Pedrinho
e o Joãozinho
. Qual deles
2
8
4
pintou mais?
1
Zezinho
2
Pedrinho 2
Joãozinho 4
4
8
1 2 4
   0,5
2 4 8
Afinal, pintaram todos a mesma porção de folha. Fracções
equivalentes são fracções que representam o mesmo número.
x4
Repara:
:4
x2
:2
1 2 4
 
2 4 8
x2
ou
1 2 4
 
2 4 8
:2
x4
:4
Princípio de equivalência de fracções: se multiplicarmos ou dividirmos
ambos os termos de uma fracção pelo mesmo número inteiro, diferente de
zero, obtemos uma fracção equivalente à dada.
Faz tu.
Por exemplo:
x3
x2
4 12

5 15
1
2

18
9
x3
x2
:5
15
3

30
6
:5
Simplificar uma fracção é, obter uma fracção equivalente com termos
menores.
Então, simplifica até ao máximo a fracção:
:2
:2
24 12 6 2

 
36 18 9 3
:2
2
3
:2
: 12
:3
ou
:3
não se pode simplificar mais. Chama-se FRACÇÃO
IRREDUTÍVEL.
2
24

3
36
: 12
Então, gostaste?
Aprendeste? Compreendeste?
Espero que sim, pois foi esse o meu objectivo.
Confesso que também me diverti a fazer estas “ Macacadas”; dei asas à
imaginação e, por momentos ( HORAS ), voltei a ser criança!
Mas, a pessoa mais importante agora és TU e como tal, espero que tenhas
chegado à minha conclusão:
A Matemática até é GIRA e a Brincar é mais fácil Aprender.
Até à próxima! ! ! !