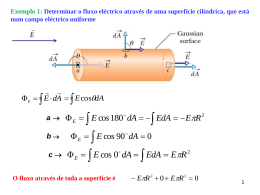
Exemplo 2
q2
Dados:
q1 = 1.5x10-3 C
q2 = -0.5x10-3 C
q3 = 0.2x10-3 C
rA = 1.2 m e rB = 0.5m
B
FR
F23
Determine a força resultante sobre a carga q3.
A
q1
C
F13
q3



q1q3 
q2 q3 
FR  F13  F23  k
e k
e
2 x
2 y
rA 
r B 
2
2

 q1q3   q2 q3 
3



FR   k

k

4
.
06
x
10
N
2 
2 

 rA    rB  
1
CAMPO ELÉCTRICO
O campo gravitacional num ponto no espaço é igual à força
gravitacional que age sobre uma partícula de prova (teste) de
massa m0 dividida pela massa da partícula de prova:

g

Fg
m0
O campo eléctrico num ponto do espaço é definido como a força
eléctrica que age sobre uma partícula de prova, colocada neste
ponto, dividida pela carga q0 da partícula de prova (teste). Assim:
Escolhemos a convenção de que uma partícula de prova tem sempre uma carga eléctrica positiva
A carga de teste serve como detector do campo eléctrico

 Fe
E
q0
O vector

E
tem as unidades SI de
newtons por coulomb (N/C)
2
Conhecendo-se o campo eléctrico num ponto P, podemos calcular a força que age sobre uma
partícula com carga q colocada nesse ponto, porque:


Fe  qE
A força exercida sobre uma carga de prova situado à uma distância r da carga q é dada pela Lei
de Coulomb:

qq0 ˆ
Fe  ke 2 r
r
O campo eléctrico criado por q no ponto P ( posição da carga de prova) é
 k qq0
e
 Fe
2 
r
E

rˆ
q0
q0


q ˆ
E  ke 2 r
r
3
Se q for positiva, o campo eléctrico estará orientado radialmente para fora a partir dela. Se q for
negativa, o campo se orientará para dentro.
Campo eléctrico num ponto P devido à um conjunto de partículas:

qi ˆ
E  k e  2 ri
i ri
Campo eléctrico num ponto P devido à uma distribuição contínua de cargas

dq ˆ
E  ke  2 r
r
4
LINHAS DO CAMPO ELÉCTRICO
As linhas de campo eléctrico é uma representação pictórica que fornece uma descrição qualitativa
do campo eléctrico.
• O vector campo eléctrico é tangente à linha do campo eléctrico em cada ponto
• O campo eléctrico é grande onde as linhas do campo estão próximas e pequeno onde as linhas
estão bem separadas  número de linhas por unidade de área é proporcional à intensidade do
campo eléctrico
LINHAS DE CAMPO PARA UMA CARGA
PONTUAL POSITIVA
 ESTÃO ORIENTADAS RADIALMENTE PARA
FORA
LINHAS DE CAMPO PARA UMA CARGA
PONTUAL NEGATIVA
 ESTÃO ORIENTADAS RADIALMENTE
PARA DENTRO
5
LINHAS DE CAMPO PARA CARGAS PONTUAIS (continuação)

E

E
 Pequenos pedaços
de fibra suspensas em
óleo se alinham com
as linhas de E
LINHAS DE CAMPO ELÉCTRICO PARA UMA CARGA PONTUAL POSITIVA E OUTRA NEGATIVA
IGUAIS:
6
LINHAS DE CAMPO ELÉCTRICO PARA UMA CARGA PONTUAL POSITIVA E OUTRA NEGATIVA
IGUAIS (continuação):
LINHAS DE CAMPO ELÉCTRICO PARA DUAS CARGAS PONTUAIS POSITIVAS
7
 LINHAS DE CAMPO ELÉCTRICO PARA UMA
CARGA POSITIVA E OUTRA NEGATIVA DIFERENTE
LINHAS DE CAMPO GERADAS POR
DUAS CARGAS NÃO UNIFORMES 
8
MOVIMENTO DE PARTÍCULAS CARREGADAS NUM CAMPO ELÉCTRICO UNIFORME

Fe
A força eléctrica resultante exercida sobre a carga é
dada por


Fe  qE
A força resultante faz com que a partícula acelere. A
segunda lei de Newton aplicada à partícula fornece


Fe  ma
A aceleração da partícula é

E

 qE
a
m
Se o campo eléctrico é uniforme (isto é, se tem magnitude e direcção constantes), a aceleração é
constante
9
Cargas libertadas do repouso, num campo eléctrico , orientado ao longo do eixo x

 qE
a
m
Se a partícula tiver carga negativa, sua aceleração será na direcção oposta à do campo
eléctrico.
Se uma partícula tiver carga positiva, sua aceleração será na direcção do campo
eléctrico.
10
Cargas eléctricas lançadas perpendicularmente à um campo eléctrico uniforme
A trajectória das cargas é uma parábola enquanto estiverem entre as placas
11
EXEMPLO
Um electrão entra numa região de campo
eléctrico uniforme (como na Figura), com uma
velocidade inicial constante, vi (fora da acção
do campo eléctrico). Obtenha a equação da
trajectória da partícula na região do campo
eléctrico.
Resolução
A aceleração da partícula no campo eléctrico é

eE 
a
ey
m


Eliminando o tempo, obtém-se a equação da
trajectória na região do campo eléctrico

y ( x)  
1 e E 2
x
2
2 me vi
12
EXEMPLO: TUBO DE RAIOS CATÓDICOS
Os electrões passam entre cada par de duas placas  uma delas carregada positivamente e outra
carregada negativamente .
As placas criam o campo eléctrico e
permitem que o feixe de electrões seja
orientado
Os electrões são deflectidos em várias
direcções
13