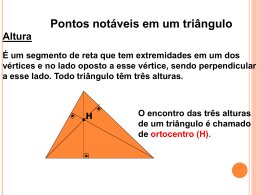
PONTOS NOTÁVEIS DE UM
TRIÂNGULO
Professora Joseane Fernandes
Pontos Notáveis de um Triângulo
 PONTOS NOTÁVEIS DE UM TRIÂNGULO.
•
•
•
•
Baricentro;
Incentro;
Circuncentro;
Ortocentro.
Pontos Notáveis de um Triângulo
 BARICENTRO - MEDIANA
Mediana – segmento de reta que liga o ponto médio de um lado ao vértice
oposto a esse lado.
A
Segmentos que representam as medianas:
Ponto médio do lado
AN , BM , CP
Baricentro – ponto de encontro das medianas.
P


M
MEDIANA
BARICENTRO
B

N
C
Pontos Notáveis de um Triângulo
 BARICENTRO - MEDIANA
 PROPRIEDADES DO BARICENTRO.
O baricentro divide a mediana de um
triângulo em duas partes, sendo que a
parte que contém o vértice é o dobro do
tamanho da que contém o ponto médio.
O baricentro é o centro de gravidade do triângulo. Isto quer dizer que, se suspendermos um
triângulo de material homogéneo pelo seu baricentro, ele fica em equilíbrio.
Pontos Notáveis de um Triângulo
 BARICENTRO - MEDIANA
 PROPRIEDADES DO BARICENTRO.
O baricentro divide qualquer triângulo
em três triângulos de mesma área.
Usando
dobradura.
Pontos Notáveis de um Triângulo
 INCENTRO - BISSETRIZ
Bissetriz – segmento de reta que une um vértice ao seu lado oposto dividindo o ângulo desse vértice ao meio.
A
Segmentos que representam as bissetrizes:
AN , BM , CP
M
P
Incentro – ponto de encontro das bissetrizes.

INCENTRO
B
N
C
Pontos Notáveis de um Triângulo
 CIRCUNCENTRO - MEDIATRIZ
Mediatriz – segmento de reta perpendicular ao lado em seu ponto médio.
O circuncentro está equidistante (à mesma distância)
dos três vértices do triângulo e é o centro de uma
circunferência circunscrita.
A

M

Circuncentro – ponto de encontro das mediatrizes.
CIRCUNCENTRO
B
N
C
Pontos Notáveis de um Triângulo
 ORTOCENTRO - ALTURA
Altura – segmento de reta perpendicular compreendido entre o vértice e o lado oposto.
A
Circuncentro – ponto de encontro das alturas.

ORTOCENTRO
B
C
Vamos praticar!
1. Considere os pontos notáveis de um triângulo: C (Circuncentro), B (Baricentro), I (Incentro) e O (Ortocentro).
Preencha os parênteses:
A) ( B ) Ponto de encontro das medianas.
B) ( C ) Ponto de encontro das mediatrizes dos lados de um triângulo.
C) ( I ) Ponto de encontro das bissetrizes internas de um triângulo
D) ( O ) Ponto de encontro das retas suportes das alturas.
E) ( B ) Ponto que divide cada mediana numa razão de 2 para 1.
F) ( I ) Centro da circunferência inscrita num triângulo.
G) ( C ) Centro da circunferência circunscrita a um triângulo.
H) ( C ) Ponto do plano de um triângulo e equidistante dos vértices desse
triângulo.
2.
Na figura, N e P são os pontos médios dos lados AC e BC, respectivamente.
Se G é o baricentro do triângulo ABC, AP = 6cm e GN = 1,5 cm, obter, em centímetros:
A) AG = 4 cm
B) GP = 2 cm
C) BG = 3 cm
D) BN = 4,5 cm
3.
No triângulo ABC, da figura, AM e CN são medianas que se interceptam em G. Sendo AG = 10 cm
e CN = 18 cm, calcule x, y e z.
x  5 cm
y  12 cm
z  6 cm
4.
Na figura, o triângulo ABC é retângulo em A e M é o ponto médio do lado BC.
Determine a medida do ângulo  .
A) 80º B) 90º C) 100º D) 110º E) 120º
5.
Um ponto P equidista dos vértices de um triângulo ABC. O ponto P representa:
A) O baricentro do triângulo ABC.
B) O incentro do triângulo ABC.
C) O circuncentro do triângulo ABC.
D) O ortocentro do triângulo ABC.
E) Um ex-incentro do triângulo ABC.
6.
Um ponto Q pertence à região interna de um triângulo DEF, equidista dos lados desse triângulo.
Então, o ponto Q representa:
A) O baricentro do triângulo DEF.
B) O incentro do triângulo DEF.
C) O circuncentro do triângulo DEF.
D) O ortocentro do triângulo DEF.
E) Um ex-incentro do triângulo DEF
7.
.
O segmento da perpendicular traçada de um vértice de um triângulo à reta suporte do lado
oposto é denominado:
A) Mediana
B) Mediatriz
C) Bissetriz
D) Altura
E) Base.
8.
Observe a figura. Baseada nas sentenças abaixo, marque a alternativa correta.
I. O triângulo CDE é isósceles.
II. O triângulo ABE é equilátero.
III. AE é bissetriz do ângulo BÂD.
A) somente a I é falsa.
B) somente a II é falsa.
C) somente a III é falsa.
D) são todas falsas.
E) são todas verdadeiras.