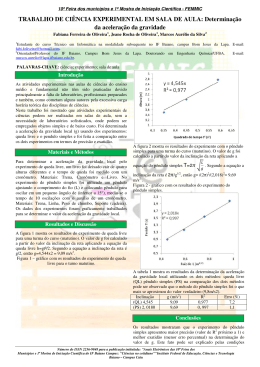
UNIVERSIDADE FEDERAL DE ALFENAS/UNIFAL-MG
EZEQUIEL FIGUEIREDO VILELA
UTILIZAÇÃO DO PLANEJAMENTO FATORIAL PARA A OTMIZAÇÃO DO
EXPERIMENTO DO PÊNDULO
ALFENAS/MG
2013
EZEQUIEL FIGUEIREDO VILELA
UTILIZAÇÃO DO PLANEJAMENTO FATORIAL PARA A OTMIZAÇÃO DO
EXPERIMENTO DO PÊNDULO
Projeto de pesquisa apresentado
como
parte
dos
requisitos
para
o
desenvolvimento estudo do Trabalho de
Conclusão de Curso, referente ao curso de
Física Licenciatura.
Orientador:
Wisniewski
ALFENAS/MG
2013
Prof.
Dr.
Célio
RESUMO
A Física experimental é uma ferramenta indispensável para o professor tanto na escola média
como na universidade, sendo a prática uma forma construtivista do conhecimento. Há
inúmeras experiências disponíveis em livros, revistas de divulgação científica, internet, entre
outros meios. Nem sempre são realizadas observações cautelosas ao se proceder com
experimentos e muitas vezes os resultados são inesperados. Por isso é preciso ter um olhar
mais crítico aos diversos fatores que podem influenciar os resultados de um experimento.
Com o objetivo de minimizar ao máximo o percentual de incertezas envolvidas em uma
prática e para que se possa aproximar aos dados da literatura, foi realizado o experimento do
pêndulo simples para determinar o valor da aceleração da força gravitacional. Planejamento
fatorial e metodologia de superfície de resposta foram utilizados com o intuito de avaliar
quais fatores foram significativos para o experimento e o valor de ótimo para os mesmos. Na
determinação da gravidade local, observou–se que o planejamento fatorial foi eficiente e os
resultados foram coerentes ao da literatura.
Palavras Chave: planejamento fatorial; experimentos no ensino médio e superior, pêndulo
simples.
ABSTRACT
Experimental physics is an indispensable tool for the teacher, both in high school and in the
university, and practice is a constructivist form of knowledge. There are innumerable
experiences available in books, science magazines, internet, and other means. Not always
careful observations are performed and lead, many times, to unexpected results. So, a more
critical look to the various factors that can influence the variables in an experiment is
necessary. With the objective of minimizing the percentage of uncertainties involved in a
practice and approach to the literature data, the simple pendulum experiment, to determine the
value of acceleration gravity force, was performed. Factorial design and response surface
methodology were used in order to assess which were significant factors for the experiment
and optimum values to them. In the determination of local gravity, it was observed that the
factorial design was efficient and results were consistent to literature.
Keywords: factorial planning; physics experiment at the high school and college, simple
pendulum.
LISTA DE FIGURAS
Figura 1- Alguns livros relacionados à prática experimental, desde a Física básica até
conteúdos de Física moderna. (Fontes: [8, 9 e 11]). .................................................................. 3
Figura 2- Diagrama de Pareto para um experimento fictício envolvendo as variáveis A, B, C
e D e suas interações. ................................................................................................................. 6
Figura 3- Planejamento em estrela com os dados codificados. Figura adaptada de (BARROS
NETO, BENICIO, 1996 [1]). .................................................................................................... 8
Figura 4 -Diagrama esquemático do pêndulo simples mostrando os valores máximos e
mínimos para as variáveis envolvidas. .................................................................................... 11
Figura 5- Representação esquemática da energia potencial para um pêndulo simples. (Fonte:
Keith R. Symon [24]) .............................................................................................................. 13
Figura 6- Pareto das interações das variáveis para o valor da aceleração da gravidade. ....... 18
Figura 7- Curvas de nível da superfície da resposta, representando os valores de concordâcia
em função do ângulo e o comprimento. .................................................................................. 20
Figura 8 – Curvas de nível da superfície da resposta para a concordância em função do
ângulo e da massa. ................................................................................................................... 21
Figura 9 – Curvas de nível da superfície da resposta para a concordância em função do
comprimento e da massa.......................................................................................................... 22
Figura 10 - Curvas de nível da superfície da resposta para a concordância em função do
diâmetro e ângulo. ................................................................................................................... 23
Figura 11 - Curvas de nível da superfície de resposta para a concordância em função
comprimento do fio e o diâmetro. ........................................................................................... 24
Figura 12- Curvas de nível da superfície de resposta para a concordância em função do
diâmetro e a massa. .................................................................................................................. 25
LISTA DE TABELAS
Tabela 1 - Matriz Doehlert para dois três e quatro fatores (valores codificados)..................... 9
Tabela 2- Níveis dos fatores no planejamento fracionário 25-1 e seus respectivos níveis de
máximo e mínimo. ................................................................................................................... 15
Tabela 3 - Ensaios realizados para o no planejamento fracionário 25-1. ................................. 16
Tabela 4 - Valores dos períodos (T1 e T2), gravidade (G1 e G2) e a concordância (C1 e C2)
obtidos nos Ensaios. ................................................................................................................ 17
Tabela 5 – Valores atribuídos na matriz de Doehlert para os 4 fatores mais influentes de
acordo com a figura 6 e resposta (C). Valores mínimos e máximos sublinhados. .................. 19
Tabela 6 – Valores obtidos da gravidade a partir dos dados fornecidos pelos gráficos
de
superfície e resposta................................................................................................................. 26
LISTA DE ABREVEATURAS E SIGLAS
CBC- Conteúdo Básico Comum;
GREF- Grupo de Reelaboração do Ensino de Física;
A.C– Antes de Cristo;
g– Aceleração da força gravitacional.
SUMÁRIO
1.
INTRODUÇÃO .................................................................................................... 1
1.1. Contextos Históricos ......................................................................................... 1
1.2. A Gravidade ...................................................................................................... 1
1.3. Laboratório de Física Ferramenta Indispensável .............................................. 2
1.4. Planejamento e otimização ............................................................................... 3
2.
JUSTIFICATIVA ............................................................................................... 10
3.
OBJETIVOS ....................................................................................................... 10
3.1. Objetivos específicos ...................................................................................... 10
4.
METODOLOGIA............................................................................................... 11
4.1. Desenvolvimento da pesquisa e de análise dos dados. ................................... 11
4.2. Desenvolvimento experimental. ..................................................................... 14
5.
RESULTADOS .................................................................................................. 17
5.1. Otimização das variáveis – quatro fatores. ..................................................... 18
5.2. Comparação método experimental clássico x planejamento. ......................... 26
6.
CONCLUSÃO .................................................................................................... 27
7.
REFERÊNCIAS BIBLIOGRÁFICAS ............................................................... 28
1
1 . INTRODUÇÃO
1.1.
Contextos Históricos
Desde os tempos mais remotos a experimentação é considerada uma maneira prática
de transformar problemas teóricos em respostas para sanar a curiosidade humana. Aristóteles
(384-322 A.C.), discípulo de Platão, analisava o que se podia observar naturalmente, na
experiência sensível humana e em seguida postulava seus princípios observáveis do
comportamento da natureza. Contudo, ele nos trouxe um conceito importante, a descrição de
movimentos, onde dizia que movimento é um processo de mudança de um corpo que passa de
um estado que se encontra para outro (atualização e corrupção). Este conhecimento mais tarde
foi descrito como “os estados inerciais” por Galileu e Descartes. Pode se dizer que no Egito
(A.C.) foram desenvolvidas as primeiras notações geométricas e desde então sendo
aperfeiçoadas cada vez mais. Os trabalhos e observações feitas na época nos parecer arcaicos,
hoje, mas foram indispensáveis para o avanço científico e desenvolvimento tecnológico que
temos nos dias atuais [2].
Em meados dos anos de 1615 a 1670, grandes nomes da ciência como Kepler, Galileu,
Newton e Leibniz, entre outros, desenvolveram métodos experimentais e cálculos que
alavancaram a ciência em geral. No início do século XVII, o conhecimento da ciência
moderna começou a se desenvolver, em relação à ciência remota e tudo encaminhou de forma
bem mais rápida. Hoje o método experimental é fundamental para qualquer comprovação
teórica científica e demonstração de um determinado fenômeno que ocorre em nosso meio
[2].
1.2.
A Gravidade
A força gravitacional ou simplesmente gravidade é descrita como uma das quatro
forças fundamentais da natureza, nos possibilitando a vida, de uma magnitude natural
impressionante e curiosa. Esta força governa o universo agindo sobre tudo que possui massa,
e utilizada para gerar diferentes tipos de energia da qual nós usufruímos. Galileu Galilei,
grande cientista que viveu nos séculos XVI e XVII, fez uma descoberta sobre a queda de
corpos com massas diferentes, observando em seu experimento que ambos caem com a
mesma velocidade, porém Galileu não sabia ao certo explicar este fenômeno [2].
2
Isaac Newton (1643-1727) descobriu a relação da força com a massa, e foi precursor
da lei da gravitação universal. Ele introduziu em sua obra, Philosophiae Naturalis Principia
Mathematica, o equacionamento desta lei, dentre outros trabalhos altamente importantes na
Física, que são utilizados nos dias atuais. Posteriormente Albert Einstein(1879-1955) explica
porquê a gravidade realizava tais fenômenos descritos por Newton, atribuindo e descrevendo
a curvatura do espaço devido à interação gravitacional de grandes massas [4 e 22].
O número de informações que a mídia nos proporciona sobre aspectos científicos
tecnológicos, referentes à gravidade, está cada vez mais frequente. Desta maneira, pode-se
trabalhar com uma série de tecnologias, que nos proporciona o desenvolvimento da ciência e
nos remete a inúmeros benefícios. O avião é um exemplo da evolução tecnológica para
superar os efeitos gravitacionais.
Podemos levantar algumas questões intrigantes para debate em sala de aula, por
exemplo; Como é possível um objeto tão grande como avião vencer a força gravitacional e
transportar toneladas? Por que é possível um satélite artificial orbitar? É possível usar a
energia gravitacional como fonte de energia?
A Agência Espacial Europeia (ESA) lançou em 2009 uma sonda com o intuito de
estudar o nosso planeta. A sonda denominada de “Gravity field and steady-state Ocean
Circulation Explorer (GOCE)” foi desenvolvida para captar com o máximo de precisão e
fazer o mapeamento da gravidade terrestre em toda a superfície do planeta. A gravidade
pode variar de 9,78 m/s2 no equador até 9,83 m/s2 nos polos, assim como possui
pequenas variações devido à altitude e à composição do subsolo. Com esta nova fonte
tecnológica foi possível obter, com precisão jamais anteriormente conseguida, o valor
real da aceleração gravitacional terrestre em todos os pontos da superfície e com isso
prover dados para outras pesquisas geofísicas [23].
1.3.
Laboratório de Física Ferramenta Indispensável
Alvarenga & Máximo [7], e o Grupo de Reelaboração do Ensino de Física (GREF)
[5], entre vários outros escritores de obras para o ensino médio e superior, nos fornecem uma
programação completa de guias para professores de Física, disponibilizando aulas em texto e
uma série de roteiros de experimentos de fácil compreensão. Os materiais que são propostos
nas obras citadas do ensino médio, geralmente são de fácil acesso e baixo custo, e o principal
foco é desenvolver habilidades lógicas dos discentes, contando também com uma série de
aspectos trabalhados pelo professor [13]. Cabe ao professor ser o intermediador dos conceitos
3
a serem desenvolvidos na prática e fazer a conexão teórico-prática esperada, sempre
trabalhando as concepções prévias já existentes pelos discentes [16].
A Educação básica atual, é permeada pelo CBC (Conteúdo Básico Comum), este
manual aborda tanto questões quanto descrições de fenômenos naturais ligados a vivência
cotidiana, sendo esta, uma peça fundamental no desenvolvimento educacional e científico [15
e 17].
A metodologia tradicional e os métodos usuais de ensino de Física trazem inúmeras
aplicações diferenciadas de roteiros experimentais, ou seja, procedimentos diferentes, mas que
alcançam o mesmo objetivo. É grande o número de obras que se referem a atividades práticas
de Física e sua relação ao conteúdo teórico, como por exemplo, as citadas na Figura 1. No
geral, existem algumas obras com embasamento mais específicos a experimentos, outras com
mais discussões teóricas, contendo questões prévias, analógicas e questões pós-prática. E
existem aquelas que trazem ambas as partes, tanto teórica quanto prática, “A Coleção do
Ensino Médio”, dos professores Antônio Máximo e Beatriz Alvarenga, por exemplo [7].
Figura 1- Alguns livros relacionados à prática experimental, desde a Física básica até
conteúdos de Física moderna. (Fontes: [8, 9 e 11]).
1.4.
Planejamento e otimização
Muitas vezes nos deparamos com situações inesperadas no decorrer das
experimentações, o que pode nos levar a conclusões precipitadas de um dado experimento.
Por exemplo a busca para alcançar os objetivos, previamente descritos, ou então a
preocupação em realizar tudo o que foi planejado no tempo destinado a sua aula. Existem
casos, em que a realização dos experimentos sem muito rigor, sem preocupações estatísticas
na elaboração do experimento e no tratamento dos resultados, também pode nos conduzir a
conclusões errôneas ou com um grau de aproximação exagerado dos valores [1].
4
Tradicionalmente estes procedimentos levam a natureza intuitiva de professores de
Física na realização de seus experimentos, utilizando roteiros determinados que não
sintetizam apropriadamente as variáveis envolvidas. Podemos notar casos como estes até
mesmo nas práticas desenvolvidas na graduação, na escola regular comum, nas quais o
experimento é feito seguindo os roteiros como uma “receita”. A falta de planejamento para
que haja resultados significativos não é levada em consideração, na maioria dos casos [6].
Além disso, muitas vezes não há uma discussão do papel de cada grandeza no experimento e
os limites para os quais estes fornecem bons resultados experimentais [12].
O professor geralmente se depara com alguns questionamentos que, em geral, são
amenizados pela prática e anos de experiência na execução do experimento. Entretanto, ao
realizar um novo experimento é necessário conhecer previamente o comportamento de
algumas variáveis do experimento [19]. Por exemplo, ao fazer a medição do valor da
aceleração gravitacional utilizando um pêndulo, logo surgem perguntas: Qual o comprimento
do fio que liga a massa ao ponto de apoio? Qual a melhor geometria e quantidade de massa?
Qual o melhor ângulo inicial da oscilação? Qual a interferência causada pelas forças de atrito
do ar com o sistema? Quantas oscilações são necessárias para medir o período do pêndulo?
Uma maneira eficiente de combater a comodidade experimental de arredondamento
de valores, postulando erros inexistentes ou poucos significativos, e ainda, atribuir os erros a
fenômenos não existentes, é desenvolver o planejamento do experimento e posteriormente a
otimização das variáveis envolvidas, para identificar os reais fatores que influenciam no
experimento [14].
O emprego de ferramentas que permitam desenvolver dados mais precisos e viáveis e
assim constatar quais variáveis influenciam o sistema pode ser útil em experimentos de Física.
Em geral somos levados a fazer somente a propagação de incertezas e avaliar o quanto
é confiável o resultado obtido ou então fazer somente uma análise matemática das equações
envolvidas obtendo–se a importância teórica de cada grandeza [20].
Para se obter a otimização de um dado experimento precisamos realizar uma triagem,
utilizando planejamento fatoriais completos ou fracionários. Estes são procedimentos
estatísticos que buscam minimizar o trabalho necessário. Com isso são eliminadas as variáveis
aqui chamadas de fatores, que não são significativas no experimento (denominados pela letra
k).
O planejamento fatorial completo consiste basicamente de realizar um levantamento
dos fatores do experimento proposto e avaliar os efeitos que os mesmos exercem um sobre o
outro e sobre o resultado final. Isto é feito de forma que os fatores variem com pelo menos
5
dois níveis (n) diferentes, ou seja, para k fatores e n ≥ 2 níveis, teremos: nk experimentos, para
dois níveis temos 2k. Exemplificando o fundamento anterior; temos um experimento que
desejamos otimizar contendo 4 fatores teremos o seguinte número de experimentos: 24 ou seja
16 experimentos. Este resultado será a quantidade de ensaios realizados e para avaliação das
incertezas envolvidas, estes serão feitos em duplicata, ou seja, duas vezes cada ensaio,
totalizando 32 experimentos, sempre realizados de maneira aleatória para evitar erros
sistemáticos nos procedimentos experimentais [10].
No planejamento fatorial completo o número de ensaios cresce a cada fator
adicionado, para experimentos com k-fatores, maior que quatro variáveis, as interações de 3
ou mais fatores não são consideradas significativas e também o número de experimentos
tornam-se muito grande e o trabalho para realizar fica muito complexo. Por exemplo, para
k = 6 temos: 26 = 64 ensaios, sendo cada vez maior o número de ensaios a medida que o valor
de k cresce. Nestes casos podemos utilizar o planejamento fatorial fracionário.
O planejamento fatorial fracionário é semelhante ao fatorial completo, usando também
dois níveis e o número de ensaios é dado por: 2k-1. Por exemplo, em um experimento que se
deseja fazer a otimização composto por 5 variáveis teremos 25-1 = 24 = 16 ensaios. Os dois
níveis de valores para as variáveis são representados pelos sinais (+) e (–), isto é, os valores
máximos e mínimos respectivamente, utilizados para avaliar o comportamento das variáveis.
Estes valores são essenciais para observar a interação entre os fatores a cada ensaio [1].
Para se obter respostas significativas é necessário fazer um levantamento preliminar
das variáveis mais significativas e fazer o planejamento fatorial identificando os níveis mais
adequados para cada fator. A observação dos efeitos de variáveis e interações entre elas é de
extrema importância para entender os processos que estão sendo monitorados em um
determinado sistema.
O diagrama de Pareto é uma representação gráfica onde podemos analisar as causas e
efeitos de um dado experimento. Com ele podemos obter as melhores interações entre os
fatores e quais destes são mais significativos no experimento. Por exemplo, no diagrama de
Pareto da Figura 2, adotamos fatores fictícias do experimento representadas por, A, B ou C.
Podemos notar a importância de cada fator através do comprimento da barra, assim
como, as interações entre os fatores, A x B, C x A e C x B. O valor p = 0,05 indica o limite de
significância, abaixo do qual a variável pode ser considerada insignificante ou sem influência
no experimento. Este recurso gráfico foi desenvolvido pelo estudioso economista italiano
chamado Pareto e as variáveis, e suas interações, são colocadas verticalmente da mais
significativa para a menos significativa. O resultado fictício abaixo nos mostra, seguindo as
6
barras horizontais de cima para baixo, que A é o fator mais significativo, logo sendo o fator
mais importante do experimento seguido pela interação de B x A, e em seguida o fator B, e
assim sucessivamente em ordem decrescente o gráfico nos indica como ocorrem os efeitos. A
interação entre C x B não é significativa neste caso, pois esta está abaixo do limite de
significância p = 0,05. Os valores positivos das barras do gráfico indicam que o efeito é
proporcional ao valor esperado da grandeza que se pretende medir, dependente destes fatores.
Figura 2- Diagrama de Pareto para um experimento fictício envolvendo as variáveis
A, B, C e D e suas interações.
A partir do diagrama de Pareto pode-se fazer a otimização utilizando os fatores mais
significativos, estudando separadamente com mais níveis, logo pode se obter mais informação
do sistema. Estes são tratados segundo a metodologia de superfície de resposta, em que
modelos matemáticos são construídos a fim de obter o ótimo experimental [3].
A análise do experimento de segunda ordem, proposto por David H. Doehlert em
1970, refere-se a esquematizações onde é possível se obter os valores de máximo ou mínimo
experimental [24]. O número de experimentos (N) necessários para a construção do modelo é
dado por K² +K+Co, sendo K o número de fatores e Co é o número de experimentos no ponto
central.
Segundo Teofilo & Ferreira (2004) [14], cada problema é definido levando-se em
conta o número de fatores e os valores codificados (X) da matriz experimental, a relação entre
os valores codificados e os reais (Y) é dado por:
7
X =
Y−X
∆X
(1)
A otimização dos fatores e feita através do planejamentos de Doehlert, que se baseiam
na metodologia de superfície de resposta, empregando funções polinomiais. Estas funções
polinomiais mais comumente utilizadas são as lineares onde é possível identificar a direção da
ocorrência do fenômeno estudado e as quadráticas que permite a observação do ponto
máximo, em diferentes superfícies gráficas.
A resposta da função linear pode ser estimada pela equação 2, os termos b0, b1 e b2,
são a s estimativas dos parâmetros do modelo e x1 e x2 referem-se as variáveis codificadas.
y = b0 + b1 x1 + b2 x2
(2)
O modelo quadrático é o mais adequado para descrever o ponto crítico, ou seja a
superfície de resposta, pois o mesmo pode se adequar a uma grande variedade de superfícies
(BOSQUE-SENDRA et al. (1995) apud DO LAGO, AYLA C, 2010, P.42) [10]. O modelo
polinomial de uma função quadrática é representado para duas variáveis pela equação 3 [1 e
10].
Y = bo + b1X1+b2X2+b11X21+b22X22+b12X1X2
O ponto estrela nada mais é do que uma outra forma do planejamento de um modelo
quadrático, porém girado em 45 graus em relação a partida, o resultado é uma distribuição
octogonal conforme a figura 3.
(3)
8
Figura 3- Planejamento em estrela com os dados codificados. Figura adaptada de
(BARROS NETO, BENICIO, 1996 [1]).
O ponto estrela possui o mesmo nível para todos os fatores, onde sua resposta mostra
os pontos centrados do ótimo experimental.
Em seguida apresentamos a matriz de Doehlert, que diferentemente do ponto estrela,
os níveis são variados para os fatores, obtendo mais informações da otimização.
Os valores codificados das matrizes do planejamento Doehlert para dois três e quatro
fatores, podem ser visualizados na Tabela 1.
9
Tabela 1 - Matriz Doehlert para dois três e quatro fatores (valores codificados).
Variáveis Experimentais – Matriz de Doehlert
Ensaios
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2 Variáveis
A
B
0
0
1
0
0,5
0,866
-1
0
-0,5
-0,866
0,5
-0,866
-0,5
0,866
A
0
1
0,5
0,5
-1
-0,5
-0,5
0,5
0,5
-0,5
0
-0,5
0
3 Variáveis
B
0
0
0,866
0,289
0
-0,866
-0,289
-0,866
-0,289
0,866
0,577
0,289
-0,577
C
0
0
0
0,817
0
0
-0,817
0
-0,817
0
-0,817
0,817
0,817
A
0
1
0,5
0,5
0,5
-1
-0,5
-0,5
-0,5
0,5
0,5
0,5
-0,5
0
0
-0,5
0
0
-0,5
0
0
4 Variáveis
B
C
0
0
0
0
0,866
0
0,289
0,817
0,289
0,204
0
0
-0,866
0
-0,289 -0,817
-0,289 -0,204
-0,866
0
-0,289 -0,817
-0,289 -0,204
0,866
0
0,577
-0,817
0,577
-0,204
0,289
0,817
-0,577
0,817
0
0,613
0,289
0,204
-0,577
0,204
0
-0,613
D
0
0
0
0
0,791
0
0
0
-0,791
0
0
-0,791
0
0
-0,791
0
0
-0,791
0,791
0,791
0,791
Fonte: FERREIRA et al., 2004.
O número de variáveis adotadas, nos dará a matriz de Doehlert, vale destacar que as
variáveis serão apenas as que representam os pontos mais significativos, obtidos no diagrama
de Pareto. Neste caso, serão feitos 21 ensaios para se obter o valor da grandeza de interesse e
otimizar os valores de A, B, C e D para obter o melhor valor da grandeza. Em outros
experimentos podemos adotar um número de variáveis diferente ou seja pode ser feito para
mais ou menos fatores, sendo adotada outra matriz de Doehlert.
O uso da planejamento em Física bem como em outras áreas é fundamental para uma
visão mais detalhada das variáveis que realmente podem afetar o experimento realizado, o
método é bem prático e simples, nos possibilitando uma compreensão do que ocorre no
experimento.
Neste trabalho investigamos o método de planejamento fracionário na determinação da
gravidade local utilizando a experiência do pêndulo simples, prosseguindo os procedimentos
10
baseados à roteiros clássicos, realização dos experimentos onde foi possível obter uma análise
estatística dos resultados esperados.
2 . JUS TIFIC ATIVA
As universidades e algumas escolas possuem laboratórios para aulas práticas, onde é
realizado experimentos que visam entender a relação entre o contexto teórico e prático, levar
ferramentas que possibilita o professor a desenvolver a aprendizagem de seus alunos. As
experiências realizadas no ambiente escolar podem ter influências tanto do meio interno
quanto externo, isto pode variar drasticamente com o uso inadequado de instrumentos e/ou
metodologias, levando a prática ao fracasso.
A análise cautelosa feita na otimização pode fornecer resultados experimentais bem
mais coerentes com os dados da literatura, assim como demonstrar aos alunos os cálculos dos
principais efeitos envolvidos e sua influência sobre o resultado final, eliminando–se
interpretações errôneas das incertezas associadas. Com isso podemos mostrar que a prática
pode ser precisa, dentro dos limites do experimento.
3 . OBJE TIV OS
Demonstrar o uso do planejamento fatorial no desenvolvimento da prática de medição
da gravidade local com o pêndulo simples e, com isso, possibilitar ao professor uma
ferramenta fundamental para verificar seus conceitos experimentais bem como as influências
das variáveis envolvidas que podem ou não trazer resultados significativos.
3.1.
Objetivos específicos
1. Desenvolver estudo das variáveis experimentais a serem realizadas e fazer o
planejamento do experimento para, em seguida, fazer a otimização;
2. Construir o diagrama de Pareto e identificar a importância de cada grandeza física
no experimento;
3. Utilizar a matriz de Doehlert, construir superfícies de resposta e otimizar as
variáveis envolvidas.
11
4 . METODOLOGI A
4.1.
Desenvolvimento da pesquisa e de análise dos dados.
Neste trabalho foi realizado o experimento para obtenção da aceleração gravitacional
local (g). Esta pratica é altamente utilizada em salas de aula e nos laboratórios de Física, por
se tratar de um tema muito importante em nosso entendimento de ciências [18].
Figura 4 -Diagrama esquemático do pêndulo simples mostrando os valores máximos e
mínimos para as variáveis envolvidas.
Para o desenvolvimento do experimento, foram identificadas as principais variáveis
que podem influenciar na medição do valor da gravidade local, tais como:
θ – o ângulo, a partir do equilíbrio, que o pêndulo será solto para iniciar o movimento
de oscilação;
M – a massa da esfera presa na ponta do fio;
O experimento foi desenvolvido a partir do planejamento fracionário da gravidade
local, trabalhando com as seguintes variáveis: ângulo (θ), massa (M) das esferas,
comprimento do fio (L), número de oscilação (Nº) e o diâmetro das esferas (D);
esquematicamente representados conforme a Figura 4.
12
O pêndulo simples pode ser construído com materiais acessíveis e de baixo custo,
neste caso empregamos os seguintes materiais: fio de náilon, transferidor, massas diferentes e
com diâmetros diferentes, um garra fixa ao teto e cronômetro.
Para que se possa chegar nos termos representativos da equação do período T, neste
experimento, devemos descrever uma série de funções envolvendo alguns conceitos de
cálculo para se obter à mesma.
Keith R. Symon em sua obra: Mecânica de 1982 [25] faz um tratamento minucioso
para o movimento pendular, levando em consideração os principais efeitos desenvolvidos e as
equações do movimento pendular. O momento de inércia no eixo z representamos aqui por
(Iz) da figura 4, é dado pela equação:
Iz = ml 2
(4)
Onde m representa a massa e l o comprimento do fio, o torque de oscilação (τz)
considerando que o ângulo de oscilação diminui é dado por:
(5)
τ z = −mgl sen θ
Substituindo (5) na equação do movimento de rotação de um corpo rígido
d
L = Izα = τ z
dt
(6)
g
l
(7)
Temos:
α = − sen θ
Onde α indica a aceleração angular, a equação (7) não é fácil de ser resolvida, porém
para pequenas oscilações do pêndulo ou seja ߠ≪ߨ/2 a equação pode ser reescrita como:
(8)
Também escrita na forma diferencial ordinária por:
d 2θ g
+ sen θ = 0
dt 2 l
(9)
A energia total do sistema é:
E=
1 2 2
ml ω − mgl (1 − cos θ )
2
(10)
13
Podemos analisar o gráfico 1 da energia potencial onde é notável que para valores
–mgl < E <mgl o movimento é oscilatório logo harmônico simples para E ligeiramente maior
que –mgl.
Figura 5- Representação esquemática da energia potencial para um pêndulo simples.
(Fonte: Keith R. Symon [24])
Para E > mgl, o pêndulo tem energia suficiente para girar em torno de um círculo
completo. Neste caso, é claro que a massa deve estar presa a uma haste rígida em vez de um
fio, a menos que θ seja muito grande. No ponto 0 este movimento é ainda periódico, pois o
pêndulo realiza uma revolução completa cada vez que θ aumenta ou diminui de 2π. A partir
da equação 10 pode–se isolar o valor da velocidade angular ω, e por conveniência tomar
como referência o ângulo invertido, isto é, o valor 1 − cos θ ⇒ cos α , sendo agora o valor
máximo de energia potencial com θ = 0 (ou na posição θmax). Isolando ω na equação 10:
1
 2g  E
 2
ω= 
+ cos α  

 l  mgl
Mas T =
2π
ω
(11)
para um ciclo completo com ω constante. Para ω dependente de α,tem–se:
dα
dT =
ω
θ max
T =4
∫
0
dα
ω
=4
1
2
l
g
θ max
∫
0
(12)
dα
(
E
mgl
+ cos α )
1
2
Onde θmax é o ângulo de oscilação máximo. O termo 4 é introduzido pois a integral é
calculada sob ¼ de ciclo. Quando o movimento é oscilatório (E<mgl), o valor máximo de E
14
em termos de α, é para a energia cinética igual a zero e energia potencial máxima. Tomando
este ângulo como sendo k:
E = −mgl (1 − cos θ max ) = −mgl cos k
1
T =4
2
l
g
θ max
dα
∫ ( cos α − cos k )
0
1
2
(13)
(14)
Esta equação pode ser resolvida em termos das integrais elípticas, na forma:
T =4
l 
k π
F  sen , 
g 
2 2
(15)
Sendo F(b,α ) é a função elíptica de Legendre do primeiro tipo definida como:
θ max
F ( b, α ) =
∫
0
Onde b= sen
dα
1 − b2 sen 2 α
(16)
k
A solução desta integral leva ao valor de T na forma:
2
T=
2
2
2

θ
l  1
3
 15 
2 θ max
4 θ max
+   sen
+   sen 6 max + ... 
1 +   sen

g  2
2 8
2  48 
2

(17)
Resolvendo a equação(17), podemos obter a exatidão para os termos da série no caso
aqui calculado para o ângulo de 10º e 40º sendo obtido a exatidão para o período com o
ângulo de, 10º de 1,00, para o ângulo de 40º a exatidão é 1,03; a medida que θ cresce a
exatidão tende a infinito ou seja para ângulo 180º, período T é infinito, pois o pêndulo se
encontra em repouso.
4.2.
Desenvolvimento experimental.
A influência dos fatores no sistema experimental, foi investigada por meio de um
planejamento fatorial fracionário 25-1, composto de 16 ensaios, considerando o número de
fatores pertinentes ao experimento nos fornecendo em duplicata 32 experimentos. Os níveis
de máximo e mínimo para os fatores de estudo estão dispostos na Tabela 2.
15
Tabela 2- Níveis dos fatores no planejamento fracionário 25-1 e seus respectivos níveis
de máximo e mínimo.
Sigla
Variáveis
Θ
Ângulo (graus)
M
Níveis
Mínimo(-)
Máximo(+)
10
40
Massa (g)
44,07
106,92
L
Comprimento (cm)
0,50
2,35
N
Número de oscilações
10
50
D
Diâmetro (cm)
5,5
9,7
Os critérios de escolha para os ângulos de 10º e 40º, são geralmente utilizados em
laboratório e as massas diferentes com as demais variáveis nos permite uma boa comparação
nos resultados entres os valores de máximo(+) e mínimo(-) para obter g.
A prática foi desenvolvida no Laboratório de Física 1, da Universidade Federal de
Alfenas (UNIFAL), com o intuito de analisar os fenômenos que ocorrem em um experimento
da aceleração da gravidade através do pêndulo simples, onde todo o ambiente da sala estava
fechado como portas e janelas, para evitar influências do meio externo.
Para confecção do pêndulo simples foi seguido os valores de máximo e mínimo
conforme consta a tabela 2. Utilizou-se bolas de isopor de diâmetros diferentes, sendo
amarrado ao fio de nylon com os respectivos comprimentos no suporte do teto, a princípio o
pêndulo está pronto. Com o auxílio de um transferidor foi possível demarcar o ângulo que se
desejava, e com isso fazer a contagem das oscilações através do cronômetro obtendo o
período (T).
Para dar continuidade no experimento, utilizou-se os dados da Tabela 3 como base,
onde cada ensaio foi realizado aleatoriamente, assim podemos evitar erros sistemáticos,
ressaltando, que é importante observar as diferentes variáveis, que alternam no decorrer de
cada ensaio, pois os valores tabelados de máximo e mínimo variam.
16
Tabela 3 - Ensaios realizados para o no planejamento fracionário 25-1.
Ensaios
Θ (graus)
M(g)
L(m)
Nº
D(m)
1
10-
44,07-
0,5-
10-
9,7+
2
40+
44,07-
0,5-
10-
5,5-
3
10-
106,92+
0,5-
10-
5,5-
4
40+
106,92+
0,5-
10-
9,7+
5
10-
44,07-
2,35+
10-
5,5-
6
40+
44,07-
2,35+
10-
9,7+
7
10-
106,92+
2,35+
10-
9,7+
8
40+
106,92+
2,35+
10-
5,5-
9
10-
44,07-
0,5-
50+
5,5-
10
40+
44,07-
0,5-
50+
9,7+
11
10-
106,92+
0,5-
50+
9,7+
12
40+
106,92+
0,5-
50+
5,5-
13
10-
44,07-
2,35+
50+
9,7+
14
40+
44,07-
2,35+
50+
5,5-
15
10-
106,92+
2,35+
50+
5,5-
16
40+
106,92+
2,35+
50+
9,7+
A aceleração da gravidade foi medida com grande cautela no Departamento de Física,
da Universidade Federal de Minas Gerais (UFMG), na cidade de Belo Horizonte MG, com
altitude média de 858 m obtendo gravidade (g) = 9,7838163±4x10-7 m/s²; este padrão é
apropriado quando comparado ao valor de (g) da cidade de Alfenas-MG, por possuir uma
altitude média de 881 m[21].
O estudo em questão foi trabalhado, com valores obtidos da gravidade(g) por meio da
concordância(C), que pode ser calculada pela equação (18), onde os valores mais próximos de
1, estão mais coerentes com o valor dado na literatura.
C = 1−
g medido − g literatura
g literatura
(18)
Utilizou-se a concordância, já que o objetivo experimental é determinar uma superfície
de resposta que possua um máximo (ou mínimo) em relação as variáveis analisadas. Desta
17
forma a concordância sempre possuirá um máximo, que é o valor concordância exata entre o
valor máximo e o valor da literatura.
5 . RE SULTADO S
Após a realização dos ensaios obtemos os períodos T1 e T2, e com isso os valores da
gravidade representada por G1 e G2, para um melhor entendimento dos valores obtidos,
fizemos a concordância C1 e C2, a partir do valor literário da UFMG, obtendo os dados
conforme a Tabela 4.
Tabela 4 - Valores dos períodos (T1 e T2), gravidade (G1 e G2) e a concordância (C1 e C2)
obtidos nos Ensaios.
T1
1,4685
1,514
1,43
1,5485
3,1085
3,29
3,0615
3,141
1,4614
1,5391
1,5637
1,4559
3,1617
3,2244
3,0705
3,1924
T2
1,477
1,507
1,427
1,5595
3,1495
3,2805
3,072
3,149
1,4605
1,5386
1,5644
1,4532
3,1628
3,2245
3,0717
3,1896
G1
9,153387
8,611484
9,652897
8,232037
9,601207
8,571085
9,898265
9,403548
9,242544
8,332898
8,072775
9,312508
9,280819
8,923388
9,840324
9,103177
G2
9,048337
8,69167
9,693526
8,116317
9,352859
8,620799
9,830717
9,355829
9,253939
8,338315
8,065553
9,347145
9,274364
8,922834
9,832637
9,119167
C1
0,935451
0,88007
0,986499
0,841291
0,981217
0,875941
0,988425
0,961017
0,944563
0,851599
0,825015
0,951713
0,948474
0,911946
0,994346
0,93032
C2
0,924715
0,888265
0,990652
0,829465
0,955836
0,881022
0,995328
0,95614
0,945727
0,852153
0,824277
0,955252
0,947814
0,911889
0,995132
0,931954
Logo em seguida obtivemos a figura 6, através do programa computacional
STATISTICA versão 7, onde podemos visualizar os fatores apresentadas por meio do
diagrama de Pareto, para o modelo quadrático.
18
Diâmetro
24.9423
Ângulo
-22.7098
Comprimento
21.70424
15.57393
Ângulo x Oscilações
Comprimento x Diâmetro
-14.794
12.73727
Massa x Diâmetro
10.14734
Massa x Comprimento
9.3141
Ângulo x Massa
Massa
9.038879
Oscilações x Diâmetro
4.537891
Oscilações
-4.49858
Massa x Oscilações
-3.99478
Comprimento x Oscilações
3.108157
Ângulo x Comprimento
-2.98016
Ângulo x Diâmetro
.5450954
p=.05
Figura 6- Pareto das interações das variáveis para o valor da aceleração da gravidade.
Seguindo as barras horizontais de cima para baixo, o resultado nos mostra os valores
positivos da figura, que representa o aumento do valor da gravidade, e os valores negativos o
inverso ou seja diminuem o valor de (g).
O diâmetro da esfera foi o mais significativo, logo, sendo o fator mais importante do
experimento, posteriormente o ângulo, que foi descrito na equação (17), da secção 4.1, o valor
negativo da barra está coerente com a equação pois ângulos menores nos dará um valor de g
mais significativo. Continuando temos o comprimento positivo, que também foi descrito na
equação (17), e esta coerente pois valores muito pequenos fornecem resultados menos
plausíveis. A massa da esfera deve ser aumentada com um percentual menor, mas cabe
ressaltar que foi significativa, na equação geral do período não empregamos a variável massa
mas como foi significativa cabe fazer a otimização desta variável. O número de oscilações foi
o menos significativo das variáveis envolvidas no estudo, e seu resultado sendo negativo com
uma taxa muito baixa, podemos fixar um número de oscilação em torno de 10, para o
processo seguinte da otimização.
5.1.
Otimização das variáveis – quatro fatores.
De posse do Pareto podemos fazer a otimização das variáveis mais influentes,
considerando que o diâmetro D, o comprimento L, o ângulo T e a massa, foram mais
significativos, realizou-se a otimização destes fatores por meio de planejamento Doehlert e
assim obtendo o valor da concordância (C).
19
Tabela 5 – Valores atribuídos na matriz de Doehlert para os 4 fatores mais influentes
de acordo com a figura 6 e resposta (C). Valores mínimos e máximos sublinhados.
Ensaios
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
D(cm)
15
25
20
20
20
5
10
10
10
20
20
20
10
15
15
10
15
15
10
15
15
T
20
20
35
25
25
20
5
15
15
5
15
15
35
30
30
25
10
20
25
10
20
L(m)
2,35
2,35
2,35
2,5
2,1
2,35
2,35
2,2
2
2,35
2,2
2
2,35
2,2
2
2,5
2,5
2,4
2,1
2,1
2,15
M(g)
158,06
158,06
158,06
158,06
209,67
158,06
158,06
158,06
106,92
158,06
158,06
106,92
158,06
158,06
106,92
158,06
158,06
106,92
209,67
209,67
209,67
C
0,998044
0,993812
0,960919
0,986441
0,981756
0,995449
0,97923
0,99404
0,983668
0,99871
0,997042
0,995034
0,959078
0,975027
0,966325
0,986441
0,999055
0,984492
0,977099
0,99926
0,985583
Com o objetivo de encontrar a região ótima do experimento ou seja a máxima ou
mínima dentro do domínio experimental, através da matriz de Doehlert podemos construir as
superfícies de respostas, as figuras abaixo representam todas as possíveis interações entre as
variáveis de estudo.
Desenvolvemos as superfícies por meio da concordância dos resultados da gravidade
em busca de melhores interpretações do experimento.
Na Figura 7, esta representada a interação dos fatores ângulo e comprimento em
relação à resposta, concordância. De acordo com a figura os valores de ótimo obtidos foram
aproximadaemente de 9º e 2,4 m para ângulo e comprimento, respectivamente de acordo com
o máximo da concordância obtido na figura, isto é, a região representada pela cor vinho. Esta
cor representa o dominio entre os pontos mais indicados para se obter o valor mais
significativo da gravidade, porém as demais regiões afastão da concordância.
20
Figura 7- Curvas de nível da superfície da resposta, representando os valores de
concordâcia em função do ângulo e o comprimento.
Na Figura 8 é mostrada a dependência da concordância em função da massa e do
ângulo. Pode–se observar que o valor máximo da superfície encontram–se próximos a uma
massa de 180 g e um ângulo em torno de 13º.
21
Figura 8 – Curvas de nível da superfície da resposta para a concordância em função
do ângulo e da massa.
Na Figura 9 é mostrada a dependência da concordância em função da massa e do
comprimento do fio. Nesta figura, observa–se claramente, que as curvas permanecem com o
valor máximo da concordância com uma massa de 190 g, semelhante à mostrada na figura 8,
e o comprimento de 2,5 m, semelhante à figura 7.
22
Figura 9 – Curvas de nível da superfície da resposta para a concordância em função
do comprimento e da massa.
Na Figura 10 é mostrada a concondância em função do ângulo e do diâmetro. O
diâmetro está próximo de de 35 cm. Percebe-se que o ângulo continua aproximado.
23
Figura 10 - Curvas de nível da superfície da resposta para a concordância em função
do diâmetro e ângulo.
Na Figura 11 é mostrada a concondância em função do diâmetro e do comprimento.
Obtemos valores de 1,9 m para o comprimento e diâmetro de 28 cm, para o máximo da
concordância.
24
Figura 11 - Curvas de nível da superfície de resposta para a concordância em função
comprimento do fio e o diâmetro.
Na Figura 12 é mostrada a concordância em função da massa e do diâmetro. Podemos
notar que os valores ótimos para esta função são de massa equivalente a
170 g e diâmetro 23 cm.
25
Figura 12- Curvas de nível da superfície de resposta para a concordância em função
do diâmetro e a massa.
Tendo os dados do ótimo experimental, foi realizado todas as possíveis funções de
interaçãos das váriaveis estudadas para a matriz de Doehlert. A partir das figuras obtivemos
os valores ótimos para a concordância em função de cada par de variáveis.
Pode-se inferir a partir dos resultados obtidosdas das superfícies de resposta que a
massa permaneceu com um valor dentro do domínio experimental em todas as figuras de
interação, no entanto, os demais fatores ficaram com uma aproximação mais defasada, mas
dentro do domíno experimental da região otima. Com isto, foram feitas possíveis
combinações entre os fatores e as respostas gráficas obtendo as respostas finais otimizadas
para os valores da tabela 6, com a respectiva concordância de resposta.
26
Tabela 6 – Valores obtidos da gravidade a partir dos dados fornecidos pelos gráficos
de superfície e resposta.
Ensaios
1
2
3
4
5
6
7
8
9
10
11
12
D(cm)
25
25
25
25
35
35
35
35
40
40
40
40
T
9
13
13
9
9
13
13
9
9
13
13
9
L(m)
1,9
2,5
1,9
2,5
1,9
2,5
1,9
2,5
1,9
2,5
1,9
2,5
M(g)
172,35
172,35
172,35
172,35
172,35
172,35
172,35
172,35
172,35
172,35
172,35
172,35
Nº
10
10
10
10
10
10
10
10
10
10
10
10
G
9,800609
9,741517
9,744157
9,79067
9,829104
9,744576
9,747665
9,744663
9,789969
9,708057
9,758212
9,79067
C
0,99819
0,995677
0,995946
0,999299
0,995371
0,995989
0,996305
0,995998
0,999277
0,992257
0,997383
0,999299
Com os valores dos fatores da Tabela acima obteve–se o valor da concordância com o
valor da literatura. Os valores de concordância destacados em negrito, tem uma concordância
muito próxima a 100%. Todos os valores são para ângulos em torno de 9º, demonstrando que
o senso comum dos docentes, em laboratório, que os melhores valores para g pode ser obtido
para valores de ângulo em torno de 10º, embora pelas figuras de resposta 7, 8 e 10, os valores
de ângulo em até 20º forneceriam valores com 98% de concordância. Podemos ainda perceber
que os valores do diâmetro entre 25 e 40 cm estão no extremo superior dos valores
considerados para as superfícies de resposta (entre 5 e 25 cm) e fornecem valores ótimos para
a concordância. Em experimentos futuros é necessário deslocar os experimentos para valores
maiores dos diâmetros e assim estabelecer uma relação melhor entre este parâmetro e a
obtenção do valor de g e com sorte, estabelecer uma relação com a força de arrasto e até uma
forma do professor estudar com seus alunos o efeito desta sobre o experimento.
5.2.
Comparação método experimental clássico x
planejamento.
O experimento otimizado nos fornecem dados mais precisos, nos levando a resultados
significativos e as variáveis mais pertinentes para serem usadas, assim coincidirem com o que
se espera do valor dado na literatura. É importante salientar que na maneira clássica
experimental é menos trabalhosa, porém um dos principais fatores negativos são os resultados
com pouca arguição a ser discutida. O máximo que o professor faz é a propagação de erros
27
para o valor do período, em função do comprimento do fio, e atribuir um erro experimental a
fatores como “resistência do ar”, “imprecisão na medição do tempo”, “ângulo de oscilação
muito grande”, entre outros.
6 . CONCLUS ÃO
Neste trabalho examinamos a interação entre as variaveis presentes no experimento do
pêndulo e os efeitos destas sobre a grandeza de resposta. Observamos que o processo de
planejamento e otimização é significativo. Os resultados encontrados nos levam a concluir
que a física experimental pode ser explorada de forma diferente pelo professor e discutir com
os alunos os efeitos de fatores que normalmente são aproximados, desprezados ou até
ignorados pelo professor, que os atribui a um único pacote como “erros experimentais
inerentes ao experimento”.
Ainda podemos destacar as concepções errôneas constantemente abordadas pelos
professores, em um dado experimento, onde é desprezado alguns fatores, porém cabe ressaltar
que a física em geral estuda a natureza e suas influências em nosso meio. Não seria
apropriado desprezar uma dada variável sem ao menos conhecer estatisticamente, seu papel
no experimento.
28
7 . RE FERÊ NCI AS BIBLIOGRÁFIC AS
[1] BARROS NETO, BENICIO. Planejamento e Otimização de Experimentos. CampinasSP, 2º ed. 1996 278p
[2] PIRES, ANTONIO S.T. Evolução das ideias da Física. 2º Edição – São Paulo: Editora
Livraria da Física, 2011.
[3] EIRAS, S. P.; COSCIONE, A. R.; ANDRADE, J C; CUSTÓDIO, R.; Métodos de
Otimização em Química. Campinas-SP: Chemkeys/ IQ-UNICAMP, 1999 (Material Didático).
[4] D.Halliday, R. Resnick e J Merrill, Fundamentos de Física, vol. II, Gravitação, ondas e
termodinâmica 4° ed. (Editora LTC, RJ: livros técnicos e científicos, 1994).
[5] GREF - Grupo de Reelaboração do Ensino de Física: (1998). Física 2 / Física Térmica /
Óptica. São Paulo/BRA: ED USP.
[6] J. PINHO-ALVES, Atividades Experimentais: Do Método À Prática Construtivista.
Tese de Doutorado em Educação, Universidade Federal de Santa Catarina, Florianópolis,
2000
[7] MÁXIMO ANTÔNIO; ALVARENGA, BEATRIZ, Física, vol. 1, 2 e 3. São Paulo:
Scipione, 2006. 1ºed.
[8] JOÃO J. PIACENTINI; BARTIRA C.S. GRANDI; MÁRCIA P. HOFMANN; FLAVIO
R.DE LIMA; ERIKA ZIMMERMANN – Introdução ao Laboratório de Física – Série
Didática – 4º Edição – 2012, Editora UFSC.
[9]
Cavalcante
A.
Marisa;
Cristiane
R.
C.
Tavolaro
EXPERIMENTAL – 2ª edição. 150 p. – Barueri/ SP- 2007.
-
FÍSICA
MODERNA
29
[ 1 0 ] DO LAGO, A. C.; MÉTODO ESPECTROFOTOMÉTRICO MECANIZADO DE
ANÁLISE “ON-LINE” BASEADO NA PRÉ-CONCENTRAÇÃO DE URÂNIO EM
NANOTUBO DE CARBONO.
[11] CAMPOS. A. A., ALVES. E. S.; SPEZIALI N. L. - FÍSICA EXPERIMENTAL
BÁSICA- Coleção Didática: UFMG 2009. 1ª Reimpressão – 2º edição revista – 231p.
ISBN:978-85-7041-663-6
[12] PAULO VICTOR S. SOUZA, PENHA MARIA C. DIAS, FILIPE P. M. SANTOS
Ensinando a natureza estatística da Segunda Lei da Termodinâmica no Ensino Médio
Revista Brasileira de Ensino de Física, v. 35, n. 2, art. 2502, 2013
[13] AGUIAR, ORLANDO; VILLANI, C. Experimentos e simulações como recursos
mediacionais no ensino de Física: reflexões no curso de experiência de formação docente no
PIBID/UFMG. In: XIV Encontro Nacional de Pesquisa em Ensino de Física, 2012, São
Sebastião, SP. Anais do XIV EPEF. São Paulo: SBF, 2012. V. 1.
[14] FERREIRA, S. L. C.; SANTOS W. N. L.; QUINTELLA, C. M. ; BARROS NETO, B. ;
BOSQUE-SENDRA, J. M.. Doehlert matrix: A chemometric tool for analytical chemistry Review. Talanta (Oxford), Elsevier, v. 63, n.4, p. 1061-1067, 2004
[15] Proposta Curricular do Estado de Minas Gerais – Conteúdo Base Comum (CBC) - Física
Ensino Médio. Disponível em: http://crv.educacao.mg.gov.br/SISTEMA_CRV/index2.aspx?
Acesso em: 10 de agosto de 2013.
[16] ROCHA, F. S.; H. A. FRAQUELLI. Roteiro para a experiência de levitação de um ímã
repelido por um supercondutor no ensino de Física. Revista Brasileira de Ensino de Física,
São Paulo, v. 26, n.1, p. 11-18, 2004.
[17] NARDI, R. /Pesquisas no ensino de Física. 3. Ed.- São Paulo: Escrituras Editora, 2004, (Educação para ciência) ISBN: 85-86303-15-1
30
[18] GASPAR, A.; Castro; Alvarenga. Um estudo sobre as atividades experimentais de
demonstração em sala de aula: proposta de uma fundamentação teórica. Enseñanza de las
Ciencias, Granada, v. extra, 2005
[19] BORGES, A. T. O papel do laboratório no ensino de ciências. Atas do I1o.
ENPEC. Lindóia São Paulo. 1-11. Nov. 1997.
[20] VUOLO, J. H. Avaliação e Expressão de Incerteza em Medição. Revista Brasileira de
Ensino de Física, vol. 21, no. 3, Setembro, 1999
[21] SOARES, D.S.L. Texto: Sobre o valor da aceleração da gravidade medido no
Departamento de Física. Disponível em: http://www.fisica.ufmg.br/~dsoares/g/g.htm acesso
em: 22 de setembro de 2013
[22] NEWTON, I. Principia: Princípios Matemáticos de Filosofia Natural - livro I. 2 ed., 1
reimpr. São Paulo: Ed USP, 2008, 328p. http://astro.if.ufrgs.br/newton/principia.pdf acesso:26
de setembro de 2013
[23] Amos, J. Texto: Cientistas fazem mapa da gravidade da Terra. Disponível em:
http://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=mapa-gravidade-da-terra
acesso: 26 de setembro de 2013
[24] DOEHLERT; D. H. Uniform shell designs. Journal of the Royal Statistical Society. Series
C (Applied Statistics), v. 19, p. 231-239, 1970.
[25] Keith R. Symon; Mecânica. Tradução de Gilson Brand Batista. –Rio de Janeiro: Campus;
1982 ISBN 85-7001-369-8