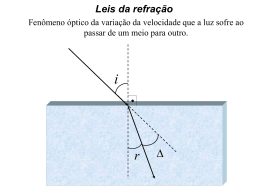
1. Introdução Teórica
a) História
b) Ângulo de Brewster
c) Relações de Fresnel
d) Aplicações
2. Prática
a) Polarização por reflexão
b) Resultados
Etienne-Louis Malus (Paris, França, 23/07/1775 – 24/02/1812)
• Engenheiro, Físico e Matemático
• 1809 - Polarização por reflexão (coeficiente de reflexão depende da polarização)
• 1810 – Estudo de birrefringência em cristais
• Lei de Malus: 𝐼 = 𝐼0 cos 2 𝜃
Lei de Malus
David Brewster (Canongate, Escócia, 11/02/1781 – 10/02/1868)
• Físico, Matemático, Astrônomo, Inventor, Escritor e Professor Universitário
• Relação entre o índice de refração e o ângulo de polarização (Ângulo de Brewster)
• Cristais biaxiais (dois eixos ópticos)
• Birrefringência por aquecimento irregular
Ângulo de Brewster
Augustin-Jean Fresnel (Broglie, França, 10/05/1788 – 14/07/1827)
• Engenheiro
• Lente de Fresnel
• 1821 – Luz é puramente transversal
• Coeficientes de Reflexão e Transmissão para cada polarização
Lente de Fresnel
Ângulo de incidência cujo raio refletido tem polarização puramente
perpendicular ao plano de incidência:
𝜃𝐵 + 𝜃𝑡 = 90𝑜
Lei de Snell:
𝑛1 sen 𝜃𝐵 = 𝑛2 sen 𝜃𝑡 = 𝑛2 cos 𝜃𝐵
𝑛2
tg 𝜃𝐵 =
𝑛1
• Lei da reflexão (𝜃𝑖 = 𝜃𝑟 )
• Lei de Snell (𝑛1 sen 𝜃𝑖 = 𝑛2 sen 𝜃𝑡 )
• Coeficientes de reflexão e transmissão para cada polarização
𝑐
𝜀0
𝜇1 ≈ 𝜇2 ⟹ 𝑣 = = 𝑐
𝑛
𝜀
𝑟∥ =
𝐸∥ tg(𝜃𝑡 − 𝜃𝑖 )
=
𝐸0 tg(𝜃𝑡 + 𝜃𝑖 )
𝑟⊥ =
𝐸⊥ sen(𝜃𝑡 − 𝜃𝑖 )
=
𝐸0 sen(𝜃𝑡 + 𝜃𝑖 )
Condições de
contorno na interface:
𝐸1𝑡
𝜀1 𝐸1𝑛
1
𝐵
𝜇1 1𝑡
𝐵1𝑛
= 𝐸2𝑡
= 𝜀2 𝐸2𝑛
1
= 𝐵2𝑡
𝜇2
= 𝐵2𝑛
𝜃𝑡 > 𝜃𝑖 𝑛1 > 𝑛2
⟹
𝑟 > 0 → 𝑠𝑒𝑚 𝑖𝑛𝑣𝑒𝑟𝑠ã𝑜 𝑑𝑒 𝑓𝑎𝑠𝑒
𝜃
1 − 𝜃𝑖
𝑛2
1
−
𝜃𝑡 − 𝜃𝑖
𝑛1
𝑡
𝜃𝑖 → 0 ⟹ 𝑟⊥ ≈ 𝑟∥ ≈
=
≈
𝜃𝑡 + 𝜃𝑖 1 + 𝜃𝑖 1 + 𝑛2
𝑛1
𝜃𝑡
𝑛1 − 𝑛2
𝑟⊥ = 𝑟∥ =
, 𝜃𝑖 → 0
𝑛1 + 𝑛2
lim
𝜋
𝜃𝑡 +𝜃𝑖 → 2
(𝜃𝑖 →𝜃𝐵 )
𝑟⊥ = sen(𝜃𝑡 − 𝜃𝐵 ) = sen 𝜃𝑡 cos 𝜃𝐵 − sen 𝜃𝐵 cos 𝜃𝑡
𝑛2
𝑛2
𝑛1
tg 𝜃𝐵 =
⟹ sen 𝜃𝐵 =
, cos 𝜃𝐵 =
𝑛1
𝑛1 2 + 𝑛2 2
𝑛1 2 + 𝑛2 2
𝜋
𝑛1
𝑛2
𝜃𝑡 + 𝜃𝐵 =
⟹ sen 𝜃𝑡 =
, cos 𝜃𝑡 =
2
𝑛1 2 + 𝑛2 2
𝑛1 2 + 𝑛2 2
𝑟∥ = 0
⟹
𝑟⊥ = sen(𝜃𝑡 − 𝜃𝐵 )
𝑛1 2 − 𝑛2 2
𝑟⊥ = 2
𝑛1 + 𝑛2 2
Coeficiente de Reflexão (𝑅 =
𝐼𝑟𝑒𝑓𝑙𝑒𝑡𝑖𝑑𝑜
𝐼𝑖𝑛𝑐𝑖𝑑𝑒𝑛𝑡𝑒
Ângulo de Brewster:
𝑛
• 𝜃𝐵 = arctg 2
𝑛1
= 𝑟 2 ):
• 𝑅∥ = 𝑟∥ 2 = 0
2
• 𝑅⊥ = 𝑟⊥ =
𝑛1 2 −𝑛2 2
𝑛1 2 +𝑛2 2
• 𝑇∥ = 1 − 𝑅∥ = 1
• 𝑇⊥ = 1 − 𝑅⊥ =
2
4𝑛1 𝑛2
𝑛1 2 +𝑛2 2 2
• Óculos de Sol
• Fotografias através de vidros e água
Polarizador alinhado com o
ângulo de polarização da luz
Alinhamento rotacionado de 90 graus
Laser
Bloco
Polarizador
Fotodetector
Voltímetro
Transmissão
Reflexão
Fitting:
𝑛
tg arcsen 1 sen 𝜃 − 𝜃
𝑛2
𝑅∥ =
𝑛
tg arcsen 1 sen 𝜃 + 𝜃
𝑛2
𝑛1
1
=
= 0,60 ± 0,03
𝑛2 𝑛∥
𝑛∥ = 1,67 ± 0,08
𝑛
sen arcsen 1 sen 𝜃 − 𝜃
𝑛2
𝑅⊥ =
𝑛
sen arcsen 1 sen 𝜃 + 𝜃
𝑛2
𝑛1
1
=
= 0,645 ± 0,005
𝑛2 𝑛⊥
𝑛⊥ = 1,55 ± 0,01
2
2
𝑛⊥ + 𝑛 ∥
𝑛𝑅 =
= 1,61 ± 0,08
2
Fitting:
𝑛
tg arcsen 1 sen 𝜃 − 𝜃
𝑛2
𝑇∥ = 1 −
𝑛
tg arcsen 1 sen 𝜃 + 𝜃
𝑛2
𝑛1
1
=
= 0,61 ± 0,04
𝑛2 𝑛∥
𝑛∥ = 1,6 ± 0,1
𝑛
sen arcsen 1 sen 𝜃 − 𝜃
𝑛2
𝑇⊥ = 1 −
𝑛
sen arcsen 1 sen 𝜃 + 𝜃
𝑛2
𝑛1
1
=
= 0,640 ± 0,007
𝑛2 𝑛⊥
𝑛⊥ = 1,56 ± 0,02
2
2
𝑛⊥ + 𝑛∥
𝑛𝑇 =
= 1,58 ± 0,06
2
𝑛⊥ + 𝑛∥
= 1,61 ± 0,08
2
𝑛⊥ + 𝑛∥
𝑛𝑇 =
= 1,58 ± 0,06
2
𝑛𝑅 =
𝑛 = 1,60 ± 0,07 ⟹ 𝜃𝐵 = 58 ± 4
Wikipedia: 1,5 < 𝑛𝑣𝑖𝑑𝑟𝑜 < 1,9 ⟹ 56,31𝑜 < 𝜃𝐵 < 62,24 𝑜
Equivalência de valores tabelados e resultados
•
Ótica Experimental – Tiago B. Batalhão, Eduardo R. de Azevêdo, Luiz Antônio de Oliveira Nunes
•
http://en.wikipedia.org/wiki/Fresnel_equations (04/05/2011)
•
http://en.wikipedia.org/wiki/Augustin-Jean_Fresnel (05/05/2011)
•
http://en.wikipedia.org/wiki/Étienne-Louis_Malus (05/05/2011)
•
http://en.wikipedia.org/wiki/Brewster's_angle (04/05/2011)
•
http://en.wikipedia.org/wiki/David_Brewster (05/05/2011)
•
http://en.wikipedia.org/wiki/Malus'_law (05/05/2011)
•
http://www.modulatedlight.org/optical_comms/fresnel_lens_comparison.html (06/05/2011)
•
http://pt.wikipedia.org/wiki/Refração (07/05/2011)