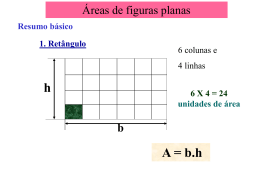
Área do triângulo
Recorda:
• a forma de calcular
a área de um QUADRADO:
• a forma de calcular
a área de um RECTÂNGULO:
Qual será a relação entre a área de um TRIÂNGULO …
… e a área do RECTÂNGULO COM A MESMA BASE
E A MESMA ALTURA?
• Constrói um rectângulo em papel de cor verde e
um triângulo (inscrito no rectângulo), em papel
vermelho, com a mesma base e a mesma altura.
• Recorta o triângulo obtendo dois triângulos mais
pequenos em papel verde como se vê na figura:
• Sobrepõe os dois triângulos novos, ao triângulo
inicial e repara que, com os dois triângulos
novos, podes formar um triângulo igual ao inicial.
Então:
+
=
Logo, o rectângulo inicial corresponde a dois
triângulos iguais.
+
=
Como podes então relacionar a área do
rectângulo com a área do triângulo, que
desenhaste, inscrito no rectângulo?
A área de um TRIÂNGULO é
METADE da área do RECTÂNGULO
com a mesma base e a mesma altura.
Generalizando, a todos os tipos de triângulos,
obtém-se a fórmula da ÁREA DO TRIÂNGULO:
Área do círculo
1. Desenha, numa folha branca, uma circunferência
com 6 cm de raio.
6 cm
2. Traça um dos seus diâmetros.
3. Contorna a preto uma das semicircunferências e a
azul-escura a outra.
4. Pinta de azul claro um dos semicírculos e de amarelo
o outro.
5. Dobra o círculo ao meio, pelo diâmetro que traçaste e
vinca.
6. Volta a dobrar ao meio.
7. Repete o passo anterior mais duas vezes.
8. Desdobra o círculo e corta-o pelo diâmetro que
traçaste.
9. Num dos semicírculos, partindo do seu centro, corta
pelos vincos os setores, tendo o cuidado de não os
separar , como mostra a figura.
10. Procede do mesmo modo no outo semicírculo.
11. Cola as duas partes no teu caderno, como mostra a
figura.
Conclusões
 A figura geométrica que colaste faz lembrar um
retângulo.
largura = raio = 6 cm
comprimento = metade do perímetro do círculo
comprimento = (π x 2 x r): 2
Comprimento = (3,14, x 2 x 6) : 2 = 18,8 cm
 A largura aproximada da figura é 6 cm, porque
corresponde ao raio da circunferência.
 O comprimento aproximado da sua base é metade
do perímetro do círculo, ou seja 18,8 cm.
largura = 6 cm
comprimento= (2 x 3,14 x 6): 2 = 18,84 cm
Área = comprimento x largura
Área = 18,84 x 6 = 113,04 cm2
 Através desta investigação podemos concluir que a
área do círculo é, aproximadamente, igual à área do
retângulo.
 Logo podemos deduzir uma fórmula para calcular a
área do círculo.
largura do retângulo (l)
=
raio do círculo (r)
comprimento do retângulo (c)
=
metade do perímetro do círculo (𝜋 x r)
Simplificando temos:
Área = c x l
Área = 𝜋 x r x r
ou seja
Área = 𝜋 x r 2
O que aprendi neste capítulo…
Agora já sei que...
Perímetro de figuras planas
• O PERÍMETRO de um polígono ou de uma qualquer
figura plana é o comprimento da linha que o delimita.
• Em particular, o perímetro do círculo é dado por:
P=×d
ou
P=2××r
(em que d e r representam, respectivamente,
o diâmetro e o raio do círculo e  = 3,141 592 65…)
Área de figuras planas
• A ÁREA de uma qualquer figura plana é a medida da
superfície que esta ocupa.
• Figuras planas com
a mesma área dizem-se
EQUIVALENTES.
• Figuras planas
com a mesma área
e a mesma forma
dizem-se CONGRUENTES.
Medidas de área
• Unidades do SISTEMA MÉTRICO:
• Correspondência entre unidades de MEDIDA DE ÁREA:
• MEDIDAS AGRÁRIAS:
1 a = 100 m2
1 ha = 10 000 m2
Cálculo da área de algumas
figuras
QUADRADO
RECTÂNGULO
TRIÂNGULO
CÍRCULO
Cálculo da área de figuras
planas
• Alguns métodos: