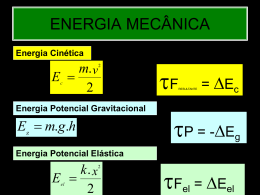
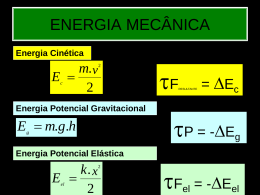
ENERGIA MECÂNICA
Energia Cinética
m. v
E 
2
2
c
Energia Potencial Gravitacional
E  m.g.h
g
F
RESULTANTE
= Ec
P = -Eg
Energia Potencial Elástica
k. x
E 
2
el
2
Fel = -Eel
CONSERVAÇÃO DA ENERGIA
MECÂNICA
Se desprezarmos os atritos:
E mec = E mec
0
f
E  E E  E  E E
c
el
g
0
0
c
0
el
g
f
f
f
Montanha Russa
Carro de massa 200 kg, deslizando em Montanha Ruusa, Freado por uma mola com K = 3.200 N/m:
a) Tabela:
Posição Emec (J)
Epg (J)
Epel (J)
Ec (J)
|V| (m/s)
A
10.000
10.000
0
0
0
B
10.000
3.600
0
6.400
8
C
10.000
8.400
0
1.600
4
D
10.000
0
0
10.000
10
E
10.000
0
6.400
3.600
6
F
10.000
0
14.400
-4.400 Não Existe!
Obs: No ponto F o caro teria Energia Cinética Negativa (Impossível) e não há solução para a sua velocidade!
b)
No ponto de deformação máxima, temos Ec = 0, ou seja Em = Epel = 10.000
K.X²/2 = 10.000 => X = 2,5 m
Montanha Russa
Real
12.000
12.000
10.000
10.000
8.000
8.000
Emec (J)
6.000
Epg (J)
Epel (J)
4.000
Ec (J)
Energia (J)
Energia (J)
Montanha Russa
Ideal
Emec (J)
6.000
Epg (J)
Epel (J)
4.000
Ec (J)
2.000
2.000
-
A
B
C
D
E
A
F
B
C
D
(2.000)
(2.000)
Posição
Posição
E
F
Bungee Jump
Curso de Física - 2ª Série-E.M.
No ponto mais alto, só
existe Energia Potencial
Gravitacional:
EM = Eg = m.g.h
EM = 24.000 J
Como estamos desprezando os
atritos, temos que a energia
mecânica deste sistema é sempre
a mesma.
Bungee Jump
Curso de Física - 2ª Série-E.M.
Nesse caso, X = X0 e X = 0
X0 = 15m
(tamanho da
corda )
a) Na altura 25 m temos:
EM = Eg +Ec = 24.000 J
60.10.25 + 60 v²/2 = 24.000 J
h1=25m
V = 300 m/s
V= 17,32 m/s
Bungee Jump
Curso de Física - 2ª Série-E.M.
Nesse caso, X = 20m e X0 = 15m.
Então X = 5m
X0 = 15m
(tamanho da
corda )
X = 5m
(deformação da
corda )
h2=20m
b) Na altura 20 m temos:
EM = Eg + Eel+Ec = 24.000 J
60.10.20+ 100.5²/2+60v²/2=24.000 J
V = 358,3 m/s
V= 18,93 m/s
Curso de Física - 2ª Série-E.M.
Bungee Jump
c) Para acharmos a aceleração,
usamos a 2ª Lei de Newton:
Fel
P
R = m.a
R = P – Fel = m.g – k. x
R = 600 – 500 = 100 N
100 = m . a = 60.a
a = 1,67 m/s² (para baixo)
Curso de Física - 2ª Série-E.M.
Bungee Jump
15 m
d) Na altura mínima, Mariana pára
por um instante (Ec=0)
Em = Eg + Eel = 24.000 J
60.10.h + 100. x²/2 = 24.000 J
X
h
Observando a figura, vemos que:
x + h = 25 m
Substituindo h = 25 – x na
equação de 2º grau, temos:
 x = 20, 7 m ou  x = -8,7 m.
Considerando apenas a solução
positiva, temos h = 4,3 m.
Curso de Física - 2ª Série-E.M.
Bungee Jump
Socorro!
15 m
X
h
e) Força máxima exercida pela
corda: (na deformação máxima)
F = K.  x
F = 100.20,7
F = 2.070 N (207 kgf!)
Curso de Física - 2ª Série-E.M.
Bungee Jump
Tomara que a
corda não
arrebente!
Fel
P
f) Aceleração máxima:
R = m.a
Fel – P = m.a
2070 – 600 = 60.a
a = 24,5 m/s²
ou
a = 2,4.g (2,4 vêzes a aceleração da
gravidade!)
Curso de Física - 2ª Série-E.M.
Bungee Jump
g) Velocidade Máxima:
Ocorre quando o corpo
pára de acelerar, ou seja,
quando: Fel = P
Fel
K.  x = m.g
P
100.  x = 600
x=6m
h = 25 - 6 = 19 m
Curso de Física - 2ª Série-E.M.
Bungee Jump
Conservação de Energia:
EM = Eg + Eel + Ec = 24.000 J
24.000 = 60.10.19 + 100.62/2 + 60.V2/2
Fel
P
V = 19,0 m/s
Bungee Jump
35,000
30,000
25,000
Energia (J)
EM (J)
20,000
Epg (J)
Epel (J)
15,000
Ec (J)
10,000
Velocidade Máxima
5,000
40
38
36
34
32
30
28
26
24
22
20
Altura (m)
18
16
14
12
10
8
6
4
2
0
Velocidade
020
018
016
014
012
010
008
006
004
002
-
Velocidade Máxima
h = 19m
Aceleração
015
010
005
000
40
-005
-010
-015
-020
-025
35
30
25
20
15
10
5
Eg = 400x10x8 = 32.000J
Ec = 400x52/2 = 5.000J
Ec = 400x102/2 = 20.000J
Eg = 400x10x3 = 12.000J
Ex. 23
Exercício 24
Exercício 24
[FUVEST] O ano de 2005 foi declarado o Ano Internacional da Física, em
comemoração aos 100 anos da Teoria da Relatividade, cujos resultados
incluem a famosa relação E = .m.c2. Num reator nuclear, a energia provém
da fissão do Urânio. Cada núcleo de Urânio, ao sofrer fissão, divide-se em
núcleos mais leves, e uma pequena parte, m, de sua massa inicial
transforma-se em energia. A Usina de Angra II tem uma potência elétrica de
cerca 1350MW, que é obtida a partir da fissão de Urânio-235. Para produzir
tal potência, devem ser gerados 4000 MW na forma de calor Q. Em relação
à Usina de Angra II, estime a
a) quantidade de calor Q, em joules, produzida em um dia.
b) quantidade de massa m que se transforma em energia na forma de
calor, a cada dia.
c) massa MU de Urânio-235, em kg, que sofre fissão em um dia, supondo
que a massa m, que se transforma em energia, seja aproximadamente,
0008 (8x10–4 da massa MU).
• E = m.c2
Essa relação indica que massa e energia podem se transformar uma na outra. A quantidade de energia E que
se obtém está relacionada à quantidade de massa Dm, que "desaparece", através do produto dela pelo quadrado da velocidade da luz (c).
• NOTE E ADOTE:
Em um dia, há cerca de 9x104 s
1MW = 106W
c = 3 x 108 m/s
Resultante Centrípeta:
Resultante das Forças na Direção Perpendicular ao Movimento
Rcp = m . V2
R
Rcp = m . acp
Resultante Centrípeta:
N
P
P>N
P - N = Rcp
Ex. 25
P - N = m . V2 / R
Resultante Centrípeta:
N
P
N>P
N - P = Rcp
Ex. 25
N - P = m . V2 / R
Resultante Centrípeta:
N
P
N + P = Rcp
N + P = m . V2 / R
Ex. 25
Resultante Centrípeta:
N
P
N = Rcp
N = m . V2 / R
Ex. 25
No ponto A, toda energia mecânica da
bolinha de massa 200g (0,2kg) esta na
forma de energia gravitacional (Eg=m.g.h)
Eg = 0,2.10.3,2 = 6,4 J
No
massa
200g
No ponto
ponto B,
C, aa bolinha
D,
bolinha de
possui
energia
2 energia cinética
(0,2kg)(Ec=m.v
só possui
cinética
C /2) e Gravitacional
D
2
(Ec=m.v
(Eg=m.g.2.R)
(Eg=m.g.R)
B /2)
No ponto A, toda energia mecânica
da bolinha de massa m esta na forma
de energia gravitacional (Eg=m.g.h0)
No ponto D, a bolinha possui
energia cinética (Ec=m.vD2/2) e
Gravitacional (Eg=m.g.2.R)
A menor altura
corresponde, então, à
menor velocidade!
Ex. 34
Resultante Centrípeta:
N
P
N + P = Rcp
N + P = m . V2 / R
Ex. 25
Se N = 0, então
m.g = m. V2 / R
V2 = g.R
X
Eg=mgh
Ec=mv2/2
Ec=0
F
TRAZER LIVRO
Apostila ex. 24 a 27