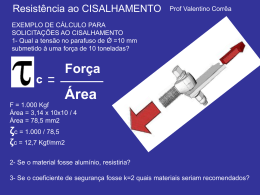
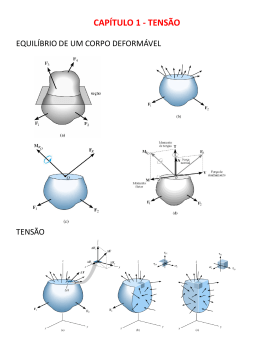
Curso de Engenharia de Produção
Resistência dos Materiais
Resistência dos Materiais
Tensão:
Consideraremos que o material é:
- Contínuo, isto é, possui continuidade ou distribuição uniforme
de matéria sem vazios,
- Coeso, o que significa que todas as suas porções estão muito
bem interligadas, sem trincas ou separações.
Resistência dos Materiais
Tensão:
Resistência dos Materiais
Tensão:
Resistência dos Materiais
Tensão:
A medida que a área ΔA tende a zero, o mesmo ocorre com a força
ΔF e suas componentes; porém, em geral, o quociente entre a força
e a área tenderá a um limite finito.
Esse quociente é denominado tensão.
Resistência dos Materiais
Tensão:
Tensão Normal.
A intensidade da força, ou força por unidade de área, que age
perpendicularmente à ∆A, é definida como tensão normal
σ (sigma).
Resistência dos Materiais
Tensão:
Tensão Normal.
Se a força normal ou tensão tracionar o elemento de área ∆A, ela
será denominada Tensão de Tração,
Se comprimir o elemento ∆A, ela será denominada Tensão de
Compressão.
Resistência dos Materiais
Tensão:
Tensão de Cisalhamento.
A intensidade da força, ou força por unidade de área, que age
tangente a ∆A, é denominada tensão de cisalhamento, τ (tau)
Resistência dos Materiais
Tensão:
Estado Geral de Tensão.
Se o corpo for ainda mais secionado por planos paralelos ao plano
x-z e pelo plano y-z, então podemos "cortar" um elemento cúbico
de volume de material que representa o estado de tensão que age
em torno do ponto escolhido no corpo
Resistência dos Materiais
Tensão:
Estado Geral de Tensão.
Resistência dos Materiais
Tensão:
Unidades.
No Sistema Internacional de Unidades de Medidas, ou Sistema SI,
os valores da tensão normal e da tensão de cisalhamento são
especificadas nas unidades básicas de newtons por metro
quadrado (N/m2).
Essa unidade, denominada 1 pascal (1 Pa = 1 N/m2)
Resistência dos Materiais
Tensão:
Unidades.
1 pascal (1 Pa = 1 N/m2), é muito pequena, e, em trabalhos de
engenharia, são usados prefixos
Quilo (10^3), simbolizado por k,
Mega (10^6), simbolizado por M,
Giga (10^9), simbolizado por G,
para representar valores de tensão maiores, mais realistas.
Resistência dos Materiais
Tensão:
Tensão normal média em uma barra com carga axial.
Premissas:
A barra permaneça reta antes e depois da aplicação da carga
A barra tem deformação uniforme quando a barra for submetida à
carga
P seja aplicada ao longo do eixo do centroide da seção transversal
Resistência dos Materiais
Tensão:
Tensão normal média em uma barra com carga axial.
Resistência dos Materiais
Tensão:
Tensão normal média em uma barra com carga axial.
Resistência dos Materiais
Tensão:
Distribuição da tensão normal média.
Cada área ∆A na seção transversal está submetida a uma força
∆F = σ∆A, e a soma dessas forças que agem em toda a área da
seção transversal deve ser equivalente à força resultante interna P
na seção. Se fizermos ∆A=dA e, portanto, ∆F= dF, então,
reconhecendo que σ é constante.
Resistência dos Materiais
Tensão:
Distribuição da tensão normal média.
Se fizermos ∆A=dA e, portanto, ∆F= dF, então, reconhecendo que σ
é constante.
Resistência dos Materiais
Tensão:
Equilíbrio.
Resistência dos Materiais
Tensão:
Tensão Normal Média Máxima.
As vezes a barra pode
estar sujeita a várias cargas
externas ao longo de seu eixo
ou pode ocorrer uma mudança
em sua área da seção transversal
Sendo necessário a determinação da Tensão Maxima a que a peça
está sujeita.
Resistência dos Materiais
Tensão:
Exemplo:
A barra na Figura tem largura constante de 35 mm e espessura de
10 mm. Determine a tensão normal média máxima na barra
quando ela é submetida à carga mostrada.
Resistência dos Materiais
Tensão:
Exemplo Solução:
Carga interna. Por inspeção, as forças internas axiais nas regiões AB,
BC e CD são todas constantes, mas têm valores diferentes.
Essas cargas são
determinadas usando
o método
Resistência dos Materiais
Tensão:
Exemplo:
Por inspeção, a maior carga está na região BC, onde P bc = 30 kN.
Visto que a área da seção transversal da barra é constante, a maior
tensão normal média também ocorre dentro dessa região.
Resistência dos Materiais
Tensão:
Exemplo:
A luminária de 80 kg é sustentada por duas hastes, AB e BC, como
mostra a Figura.
Se AB tiver diâmetro de 10 mm
e BC tiver diâmetro de 8 mm,
determine a tensão normal
média em cada haste.
Resistência dos Materiais
Tensão:
Exemplo:
A peça fundida mostrada na Figura
é feita de aço, cujo peso específico
é 'γaço = 80 kN/m3. Determine a
Tensão de compressão média que
age nos pontos A e B.
Resistência dos Materiais
Tensão:
Tensão de cisalhamento média
A tensão de cisalhamento foi definida como a componente da
tensão que age no plano da área secionada.
Resistência dos Materiais
Tensão:
Tensão de cisalhamento média
Um diagrama de corpo livre
do segmento central não
apoiado da barra indica que
a força de cisalhamento
V = F/2 deve ser aplicada a
cada seção para manter o segmento
em equilíbrio.
Resistência dos Materiais
Tensão:
Tensão de cisalhamento média
A tensão de cisalhamento média distribuída sobre cada área
secionada que desenvolve essa força de cisalhamento é
definida por:
τ méd = tensão de cisalhamento média na seção,
que consideramos ser a mesma em cada ponto
localizado na seção
V = força de cisalhamento interna resultante na seção
determinada pelas equações de equilíbrio
A = área na seção
Resistência dos Materiais
Tensão:
Tensão de cisalhamento média :
Uma investigação mais exata da distribuição da tensão de
cisalhamento na seção crítica revela, muitas vezes, que
ocorrem tensões de cisalhamento no material muito maiores
do que as previstas por essa equação. Embora isso possa
acontecer, de modo geral, aceitável para muitos problemas de
engenharia envolvendo projeto e análise.
Resistência dos Materiais
Tensão:
Cisalhamento Simples:
Cisalhamento Duplo:
Resistência dos Materiais
Tensão:
Exercicio:
A barra mostrada na Figura 1.24a tem área de seção
transversal quadrada com 40 mm de profundidade e largura.
Se uma força axial de 800 N for aplicada ao longo do eixo que
passa pelo centroide da área da seção transversal da barra,
determine a tensão normal média e a tensão de cisalhamento
média que agem no material ao longo do (a) plano de seção aa e do (b) plano de seção b-b.
Resistência dos Materiais
Tensão:
Exercicio:
Resistência dos Materiais
Tensão:
Exercicio:
Resistência dos Materiais
Tensão:
Exercicio:
Parte (a)
Carga interna. A barra é secionada em a, e a carga interna
resultante consiste somente em uma força axial para a qual P =
800 N. Tensão média. A tensão normal média é determinada
pela Equação
Resistência dos Materiais
Tensão:
Exercicio:
Parte (a)
Não existe nenhuma tensão de cisalhamento na seção,
visto que a força de cisalhamento na seção é zero.
Resistência dos Materiais
Tensão:
Exercicio:
Resistência dos Materiais
Tensão:
Exercicio:
Parte (b)
Carga interna. Se a barra for secionada ao longo de b-b, o
diagrama de corpo livre do segmento esquerdo é mostrado
na Figura. Neste caso, a força normal (N) e a força de
cisalhamento (V) agem na área secionada.
Resistência dos Materiais
Tensão:
Exercicio:
Resistência dos Materiais
Tensão:
Exercicio:
Tensões médias. Neste caso, a área secionada tem espessura
e profundidade de 40 mm e 40 mm/sen 60° = 46,19 mm,
respectivamente. Portanto, a tensão normal média é
Resistência dos Materiais
Tensão:
Exercicio:
A escora de madeira mostrada na Figura está suspensa por
uma haste de aço de 10 mm de diâmetro que está presa na
parede. Considerando que a escora suporta uma carga vertical
de 5 kN, calcule a tensão de cisalhamento média na haste na
parede e ao longo dos dois planos sombreados da escora, um
dos quais é indicado como abcd.
Resistência dos Materiais
Tensão:
Exercicio:
Resistência dos Materiais
Tensão:
Exercicio:
Resistência dos Materiais
Tensão:
Exercicio:
Como mostra o diagrama de corpo livre na Figura, a haste
resiste à força de cisalhamento de 5 kN no local em que está
presa à parede. A Figura c mostra um diagrama de corpo livre
do segmento secionado da escora que está em contato com a
haste. Aqui, a força de cisalhamento que age ao longo de
cada plano sombreado é 2,5 kN.
Resistência dos Materiais
Tensão:
Exercicio: