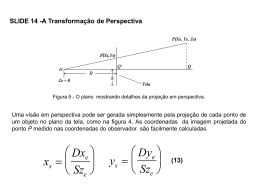
Transformações Geométricas
 Monge - 1801 - Geometrie Descriptive
 Em Computação Gráfica exprimimos estas transformações através da Geometria Afim:
• as coordenadas de um ponto P’(x’, y’, z’), resultante
de uma transformação afim aplicada ao ponto
P(x,y,z), são obtidas através de uma função linear
do tipo:
P’ = M . P + B
• A Geometria Afim transforma:
– retas paralelas em retas paralelas
– pontos finitos em pontos finitos
 Transformações afins: translação, rotação, escalamento, espelhamento e cizalhamento
Transformações Geométricas
P’ = M . P + B
x’
y’
z’
=
a11
a21
a31
a12
a22
a32
a13
a23
a33
x
y
z
+
b1
b2
b3
 No caso das transformações 2D, a matriz M reduz-se a
uma matriz 2 X 2.
 A cada tipo de transformação, corresponde uma matriz
M diferente.
Translação
 Um objeto é transladado, transladando-se todos os
seus pontos.
 Um segmento de reta é transladado, transladando-se
os seus pontos extremos, e traçando-se uma nova
linha entre eles.
P = (x,y)
y
x’= x + dx
y’= y + dy
P’
y’
P’ = P + T
dy
y
P
dx
x
dx
x’
x
T =
dy
Transformações afins
• Rotação - Movimenta um ponto através de uma rotação efetuada em torno da origem das coordenadas.
• Escalamento - transforma um objeto em um outro
menor e mais próximo da origem
y
y
> 0
P
x
P’
x
Transformações afins
 Espelhamento - é a rotação em torno de um eixo, de tal
forma que é gerada a imagem especular do objeto.
Pode-se também fazer o espelhamento em torno de um
segmento genérico qualquer.
 Cizalhamento - provoca a deformação do objeto, mantendo, entretanto, uma direção paralela.
y
y
Cizalhamento
na direção x
Espelhamento
em torno de um
segmento genérico
x
x
Coordenadas Homogêneas
 As matrizes apresentadas não permitem que se combinem transformações facilmente, isto é, pela multiplicação das matrizes de transformações geométricas correspondentes a cada transformação.
 As coordenadas homogêneas permitem que este efeito
possa ser obtido.
mapeamento de
N em N+1
espaço N
[ a b]T
espaço N+1
[ aw bw w]T
Coordenadas Homogêneas
 Quando se exprimem pontos em coordenadas
homogêneas, as transformações geométricas podem
ser tratadas todas de uma mesma forma, como
multiplicações:
P’ = M . P
 M é chamada Matriz de Transformação.
 P é da forma [ x y 1]T e w foi tomado com o valor
arbitrário 1.
projeção de
N+1 em N
espaço N
[ a/w b/w]T
espaço N+1
[ a b w]T
Translação
x’
y’
1
1
0
0
=
0
1
0
dx
dy
1
x
y
1
T(dx, dy)
 Como se processa um conjunto de translações?
dx1
dy1
P
dx2
dy2
P’
P’’
 A matriz M, que leva de P a P’’, é dada pelo produto
T1 . T2, ou seja, T(dx1+dx2, dy1+dy2) . T é dita Matriz
Composição de T1 e T2
 Translações sucessivas são aditivas.
Escalamento
x’
y’
1
Sx
0
0
=
0
Sy
0
0
0
1
x
y
1
S(Sx, Sy)
 Como se processa um conjunto de escalamentos?
Sx1
Sy1
P
Sx2
Sy2
P’
P’’
 A matriz M, que leva de P a P’’, é dada pelo produto
S1 . S2, ou seja, S (Sx1.Sx2, Sy1.Sy2). M é dita Matriz
Composição de S1 e S2
 Escalamentos sucessivos são multiplicativos.
Rotação
x’
y’
1
cos sin 
sin  cos 
0
0
=
0
0
1
x
y
1
R ()
 Como se processa um conjunto de rotações?
1
P
2
P’
P’’
 A matriz M, que leva de P a P’’, é dada pelo produto
R1 . R2, ou seja, R (1 + 2).
 Rotações sucessivas são aditivas.
Composição de transformações
 Exemplo: Rodar um objeto em torno de um ponto P1.
 Neste caso, M será dada pelas seguintes transformações:
• Transladar P1 para a origem
• Rodar o objeto do ângulo estipulado
• Transladar da origem para P1
M = T(x1, y1) . R ( ) . T (-x1, -y1)
T (-x1, -y1)
P1
R ( )
T(x1, y1)
P1
 Os produtos não são comutativos
P1
Considerações sobre eficiência
 A Matriz Composição de translações, rotações e
escalamentos tem a forma geral:
r11
r21
0
r12
r22
0
tx
ty
1
composição de R e S
 Multiplicar M por P para calcular P’ exige 9 multiplicações (ponto flutuante) mais 6 adições. É mais eficiente fazer:
x’ = r11 . x + r12 . y + tx
y’ = r21 . x + r22 . y + ty
 Usando-se estas fórmulas serão feitas 4 multiplicações
mais 4 adições
Mudança de sistema de coordenadas
 Sistema de coordenadas locais - o de um objeto; por
exemplo, o de uma peça de mobiliário (cadeira, mesa)
 Sistema de coordenadas universais - o da cena; por
exemplo, da sala que está sendo mobiliada.
 Uma mudança de coordenadas é feita de um sistema
“J” para um sistema “I”, transformando-se os eixos de
“I” nos eixos do sistema “J”. A Matriz Composição que
permite estas transformações deve ser aplicada a
todos os objetos do sistema “J”.
P
8
4
2
P1 = (10,8) 5
P2 = (6,6)
P4 = (4,2)
2
4
2
1
4
10
Para transformar do
sistema 2 para o sistema 1, transladamse os eixos de 1 até
coincidirem com os
de 2 -> T(4,2)
Mudança de sistema de coordenadas
 Para transformar de “J” em “I”, tem-se:
j
Pi = M i
j . P
 Para transformar de “I” em “J”, tem-se:
-1
Pj
=M
i
j
. Pi
 Sempre existem as matrizes inversas das matrizes de
transformação
 Para transformar do sistema 4 para o sistema 1, é
necessário aplicar-se rotação e escalamento, porque
as divisões de escala neste sistema são a metade de
cada divisão do 1. Ver detalhes no livro do Foley.
 Estas matrizes são utilizadas nos problemas de
composição de objetos.
Transformações 3D
 É uma generalização do problema 2D. As matrizes de
translação e escalamento recebem uma componente
correspondente à coordenada z, e as matrizes se
tornam 4 X 4.
 A rotação no espaço é decomposta em três componentes: uma relativa a cada eixo.
y
> 0
z
Regra da mão
direita
x
Transformações 3D
cos() -sin() 0 0
Rz() = sin() cos() 0 0
0
0
1 0
0
0
0 1
Rx() =
cos()
Ry() = 0
- sin()
0
0
1
0
0
sin()
0
cos()
0
1
0
0
0
0
0
0
1
0
0
0
cos() -sin() 0
sin() cos() 0
0
0
1
Matrizes inversas
A matriz T(dx, dy,dz) tem como matriz inversa:
T(-dx, -dy, -dz)
A matriz S(Sx, Sy, Sz) tem como matriz inversa:
S( 1 , 1 , 1 )
Sx
Sy
Sz
A matriz R() tem como inversa a matriz:
R (- ) = RT ()
Rotação em torno de uma linha no
OpenGl
Exemplo: Rodar um objeto de 45o em torno de
uma linha que liga a origem ao ponto (1,2,3),
mantendo fixo o ponto (4,5,6).
primitivas
Model-view
Projection
Pipeline OpenGl
glMatrixMode(GL_MODELVIEW)
glLoadIdentity ( ) ---------------------------- C = I
glTranslatef(4.0,5.0,6.0) ------------------- C = C * T(P)
glRotetef(45,1.0,2.0,3.0) ------------------- C = C * R (45)
glTranslatef(-4.0,-5.0,-6.0) ---------------- C = C * T(-P)
Matriz Model-view
Matriz de transformações genéricas
 A Matriz Composição de translações, rotações e
escalamentos tem a forma geral:
r11
r21
r31
0
r12
r22
r32
0
r13 tx
r23 ty
r33 tz
0 1
composição de R e S
 Problema: Transformar o sistema 1 no sistema 2
y
P3
1
P1
z
y
P3
P2
x
2
P2
z
P1
x
Complementação
As transformações de translação e rotação são
chamadas transformações rígidas porque não
deformam o objeto. Já a transformação de escala e o cizalhamento deformam o objeto, alterando o tamanho ou os ângulos.
1
a
0
SHx = 0
1
0
0
0
1
Obs: A transformação de x é proporcional a y
SHy
1
= b
0
0
1
0
0
0
1
Referências Bibliográficas
Foley et al. Cap. 5
Correia, A. M. de A. Perspectivas de superfícies poliédricas auxiliadas por computador.
Escola Politécnica da Universidade de São
Paulo, São Paulo, SP. Dissertação de Mestrado, 1991. (Departamento de Eng. de Construção Civil)